多分類問題學習器拆分策略

對於 $N$個類別 $C_1,C_2$

一對一（One vs. One, OvO）

將 $N$個類別兩兩配對，產生 $N(N-1$

多個二分類學習器預測得到結果中，最多的類別作為最終的分類結果。

一對其餘（One vs. Rest, OvR）

每次將一個類別作為正例，其餘其他類別樣例均作為反例，產生 $N$個二分類任務；

若有多個二分類器預測為正類，則通常考慮各分類器的預測置信度，選擇置信度最大的類別作為分類結果。

多對多（Many vs. Many, MvM）

每次將若干個類作為正類，若干個其他類作為反類，MvM的正反類構造必須有特殊的設計，不能隨意選取；

最常用的MvM技術是：糾錯輸出碼（Error Correcting Output Codes, ECOC）;

ECOC工作過程主要分為2步：

• 編碼：對 $N$個類別做M次劃分，每次劃分將一部分類別劃為正類，一部分劃為反類，從而形成一個二分類訓練集；這樣一共產生 $M$個訓練集，可以訓練出 $M$個分類器；
• 解碼： $M$個分類器分別對測試樣本進行預測，這些預測結果標記組成一個編碼；將這些預測結果編碼與每個類別各自的編碼進行比較，返回其中距離最小的類別作為最終預測結果；

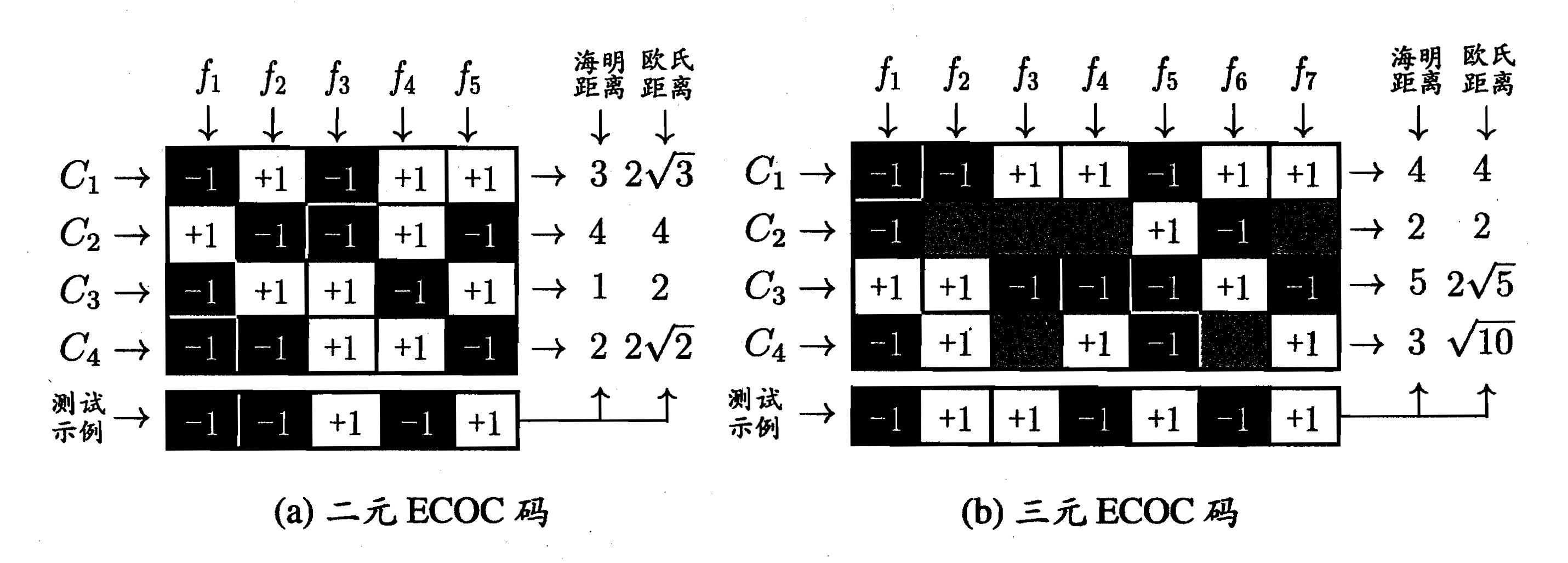
上圖是ECOC編碼示意圖，其中， $C_i$表示第 $i$個類別， $f_i$表示第 $i$個學習器，“+1”和“-1”分別表示學習器 $f_i$將該類樣本作為正、反例，“0”（三元碼中， $C_2$行 $f_2,f_3,f_4,f_7$列， $C_4$行 $f_3,f_6$列）表示學習器 $f_i$不使用該類樣本，測試示例即各學習器預測結果編碼。

海明距離：在資訊編碼中，兩個合法程式碼對應位上編碼不同的位數稱為碼距；

歐式距離：是一個通常採用的距離定義，指在m維空間中兩個點之間的真實距離；

二元ECOC碼：

測試示例：-1 -1 +1 -1 +1

$C_1$編碼： -1 +1 -1 +1 +1 海明距離 = 3 歐式距離 = $\sqrt{0+2^2+2^2+2^2+0}=2\sqrt{3}$

$C_2$編碼： +1 -1 -1 +1 -1 海明距離 = 4 歐式距離 = $\sqrt{2^2+0+2^2+2^2+2^2}=4$

$C_3$編碼： -1 +1 +1 -1 +1 海明距離 = 1 歐式距離 = $\sqrt{0+2^2+0+0+0}=2$

$C_4$編碼： -1 -1 +1 +1 -1 海明距離 = 2 歐式距離 = $\sqrt{0+0+0+2^2+2^2}=2\sqrt{2}$

$C_3$對應的海明距離和歐式距離均最小，因此最終結果為 $C_3$類。

三元ECOC碼：

測試示例：-1 +1 +1 -1 +1 -1 +1

$C_1$編碼： -1 -1 +1 +1 -1 +1 +1 海明距離 = 4 歐式距離 = $\sqrt{0+2^2+0+2^2+2^2+2^2+0}=4$

$C_2$編碼： -1 0 0 0 +1 -1 0 海明距離 = 2 歐式距離 = $\sqrt{0+1^2+1^2+1^2+0+0+1^2}=2$

$C_3$編碼： +1 +1 -1 -1 -1 +1 -1 海明距離 = 5 歐式距離 = $\sqrt{2^2+0+2^2+0+2^2+2^2+2^2}=2\sqrt{5}$