剛好專案有需求要使用到,瞭解後覺得挺有意思的就發出來跟大家分享下,主要還是為了以後自己可以回頭翻翻,大神勿噴啊

下面開始進入正題:

一個原始字串,經過不斷的修改,刪除最後變成另外一個字串,怎麼體現出這個字串的修改痕跡呢,這裡面有個最小路徑的概念,也就是原始字串->目標字串最少要經過多少步驟

假設原字串:src="abCd";

假設新字串:dst="ABCD";

那麼從abCd->ABCD最少需要經過多少步呢?

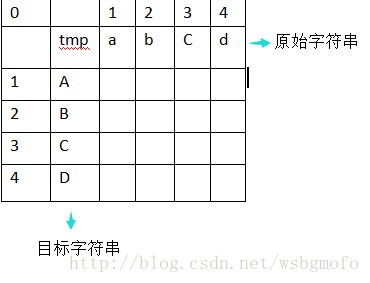
首先,我們先畫個矩陣圖形來加深理解,如下圖

1234表示字串中每一個字元對應的位置,不一定原始字串就跟目標字串一樣長,有可能原始字串比目標字串長,也可能短,這裡為了方便演示就選擇了一樣長

tmp為中間值,為了後面的計算

然後開始演算法,這個演算法是哪位資料家提出來的我忘記了,有知道的小夥伴可以留言告知下哈

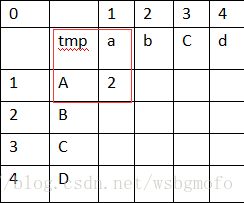
其中有個最小值的概念,以4個小正方形為一組,我們先算出第一個格子的值,如下圖

上面紅框框出來的小正方形中的2怎麼算出來的呢,可以看個式子:"a" == "A" ? 0 : 2, 這個式子的意思就是字串a是否等於字串A,如果相等,那麼結果等於0,如果不等,結果等於2,這裡的0跟2可以隨意定義,只是為了區分.

然後這裡就有3個值,分別為

起始值=0,a=1,A=1,tmp=2,

起始值+tmp=2, a+1=2, A+1=2 算出來的3個值中最小的一個值為2,這就是最小值的概念

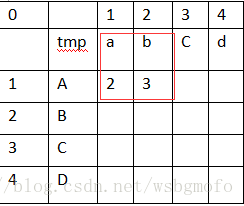
接著算出右邊第二個格子的值,如下圖所示:

按照剛才的演算法我們再來算一次,字串"b"是否等於字串"B",結果為false,那麼tmp=2,

現在4個小正方形的其他3個值為:a=1,b=2,A=2,然後a+tmp=3,b+1=3,A+1=3,最小值就是3

按照這個方式一直算下去...

.

.

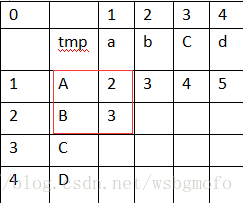
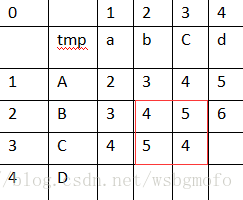
來到第二行的第一個值,還是一樣的,上圖中紅框框出的小正方形中已知的3個值分別是A=1,B=2,a=2,

"a" == "B" ? 0 : 2 結果tmp=2, 那麼 A+tmp=3,B+1=3,a+1=3,最小值是3

到了這裡大家也許會說算出來的幾個值都是相等的呀,這是因為這裡給的例子比較簡單,繼續算下去就知道了

.

.

不同的地方就在這裡了,這一步是算到原始字串中的"C"和目標字串中的"C"做比較,還是按照上面的演算法

這時小正方形裡已知的3個值分別是:

"C" == "C" ? 0 : 2 tmp=0,這裡"C" == "C" 結果為true,所以tmp=0

然後4+tmp=4,C+1=6,C+1=6,最小值就是4了

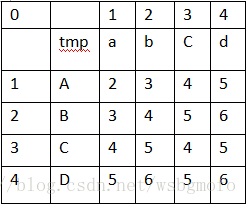
我們按照這個演算法先把矩陣填滿,如下圖所示:

上圖所示的圖形,就是我們算出來的原始字串src="abCd"到目標字串dst="ABCD"的編輯距離矩陣

矩陣中,右下角的6標識原始字串"abCd"->"ABCD"最少需要編輯6次

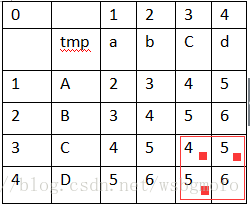
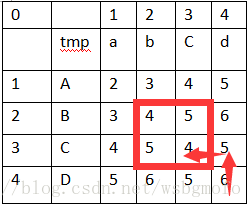
下一步,我們來根據這個距離矩陣來推匯出編輯路徑,還是以4個小正方形為一組,從右下角推導至左上角,如下圖所示:

這裡也有一個最小值,這裡的最小值是通過上圖所示紅框中帶紅點的3個值中最小的一個值

上圖所示紅框中最小值tmp=4,然後這個最小值要跟這個紅框中其他3個值一一比較,比較出來的結果按照以下方式歸類

tmp == 右上角的值 ? 向上回溯

tmp == 左下角的值 ? 向左回溯

tmp == 右下角的值 ? 向左上回溯

如果tmp都不等於他們的任何一個,那麼就用左下角的值跟右上角的值比較

右上角的值 <= 左下角的值 ? 向上回溯 : 向左回溯

按照上面的規則,我們先來算下上圖中紅框的結果

已經算出上圖紅框中的最小值tmp=4,因為tmp不等於任何一個,所以繼續比較左下角的值跟右上角的值

因為左下角的值為5,右上角的值為5,

所以 "右上角的值 <= 左下角的值 ? 向上回溯 : 向左回溯" 在這個表示式中的結果是true,所以第一步是向上回溯,如下圖所示:

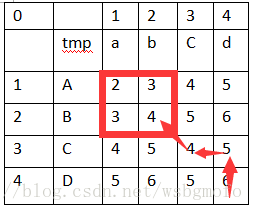
這個時候,我們的起點就停留在了上圖中紅框裡右下角的位置,繼續按照剛才的方法推導

先算出左上角,右上角,左下角3個值中的最小值,也就是,5,6,4中的最小值,tmp=4

可以看出tmp == 左下角的值,那就是向左回溯,如下圖:

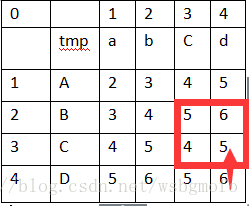
這個時候,我們的起點就在上圖所示紅框中的右下角位置,繼續按照剛才的方法

4,5,5,中最小值tmp=4,等於右下角的值,向左上回溯,如下圖:

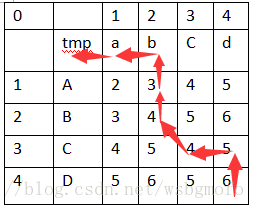
這個時候的起點就在上圖中紅框的右下角,繼續按照剛才的方法推導下去,最終如下圖:

到這裡,也許會有小夥伴問,不是算出來從原始字串到目標字串最少有6步麼,怎麼圖中會有7個箭頭,別急,我們按照反向推匯出來的路徑,正向再推導一次

第一步:從0,0->0,1,原字串刪除了"a"字元 (左移刪除)

第二步:從0,1->0,2,原字串刪除了"b"字元 (左移刪除)

第三步:從0,2->1,2,原字串增加了"A"字元 (下移增加)

第四步:從1,2->2,2,原字串增加了"B"字元 (下移增加)

第五步:從2,2->3,3,原字串中"C"字元保持不變,不計算步驟,所以步數還是從第五步開始 (右下移,不變)

第五步:從3,3->4,3,原字串刪除了"d"字元 (左移刪除)

第六步:從4,3->4,4,原字串增加了"D"字元 (下移增加)

所以原始字串"abCd"->目標字串"ABCD"就是經過了上面的6個步驟變化而來

到這裡,我們編輯距離矩陣已經講完了,大家可以根據上面講述的方法去測試任何2個字串算出他們之間的編輯路徑

附上java如何使用編輯距離矩陣的原理,體現出修改痕跡的效果,如下圖所示

黑色字體表示字串沒有改動,紅色表示新增的字元,藍色橫線表示刪除的字元

以下是資源路徑:http://download.csdn.net/download/wsbgmofo/10205970