1、樹

樹是一種很常見的分線性資料結構，公司的組織架構，行政區劃結構等都是樹形結構。樹形結構裡常見的有樹和二叉樹。

樹的定義

樹是n（n>=0）個結點的有限集。

在任意一棵非空樹中：

（1）有且僅有一個特定的稱為根（root）的結點

（2）當n>1時，其餘結點可分為m（m>0）個互不相交的有限集，其中每一個集合本身又是一棵樹，稱為根的子樹（遞迴的過程）

如上圖所示：

圖3-1是n=0的樹；

圖3-2是n=1只有一個根節點的樹；

圖3-3是一棵普通的樹，B為根節點的樹T₁ = {B，E，F，J} 是A的子樹，B為T₁的根節點，同時也有自己的子樹。

樹的3種表示方法

如圖所示的樹有以下3中表示方法：

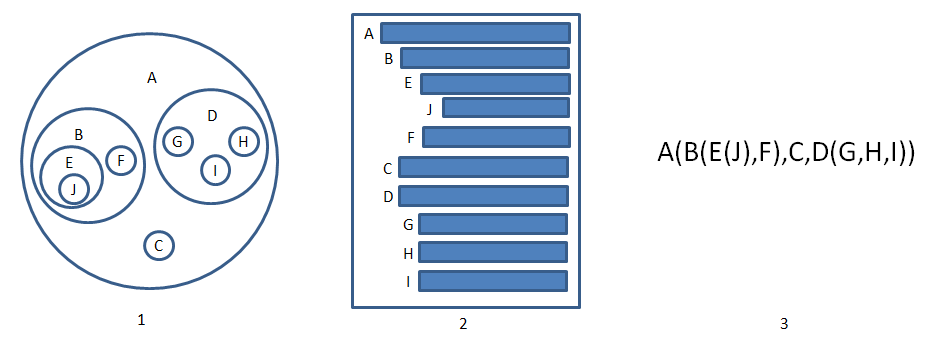
其中1是集合形式看起來很清晰；2是層級表示方式，類似書的目錄；3是一種廣義表的表示方法。

樹的一些概念

結點：包含一個數據元素 及 若干指向其子樹的分支。

例如結點B，包含了結點資料B 和 指向子樹E和F的分支。

度：結點擁有的子樹數稱為結點的度。

例如：結點B包含了兩個子樹，度為2；結點D包含了3個子樹，度為3.

葉子（終端結點）：度為0的結點（沒有子樹的結點）

　　例如：J、F、C、G、H、I都是樹的葉子。

分支結點（非終端結點）：度不為0的結點（有子樹的結點）。除了根節點外，分支結點也成為內部結點。

　　例如：A、B、E、D為分支結點；B、E、D為內部結點。

樹的度：樹內各個結點的度的最大值。

　　例如：A的度為3；B的度為2；D的度為3，其餘結點度為0，所以樹的度為3。

孩子：結點的子樹稱為結點的孩子，反過來，該節點稱為孩子的雙親。

　　例如：結點A有B、C、D 3個孩子，A是B、C、D的雙親結點。

兄弟：同一雙親的孩子互為兄弟。

祖先：從根節點到某個結點（N）經歷的所有結點稱為該節點（N）的祖先；反之，以某結點（N）為根的任一結點都是該節點（N）的子孫。

堂兄弟：雙親結點在同一層的結點互為堂兄弟。

　　例如：E 和 G、H、I為堂兄弟。

結點的層次：結點的層次是從根節點開始，根為第一層，依次遞增，所以上面樹的結點A在第1層，J在第4層。如果結點在n層，其子樹（如果有子樹）就在第n+1層。

樹的深度（高度）：樹種結點的最大層次稱為樹的深度（Depth）或高度。上面樹的深度為4。

有序樹：如果樹中結點的各子樹從左到右是有次序的（即不能互換），則次樹是有序樹；反之，則為無序樹。

2、二叉樹（Binary Tree）

二叉樹是一種有限制的樹，每個結點最多隻有兩顆子樹（即二叉樹中不存在度大於2的結點），並且二叉樹的子樹有左右之分，次序不能任意顛倒。

可以簡單理解為：二叉樹是一棵任意結點度不大於2的有序樹。

二叉樹有以下5中結構：

1：空二叉樹；

2：只有根節點的二叉樹；

3：右子樹為空的二叉樹；

4：左右子樹均非空的二叉樹；

5：左子樹為空的二叉樹

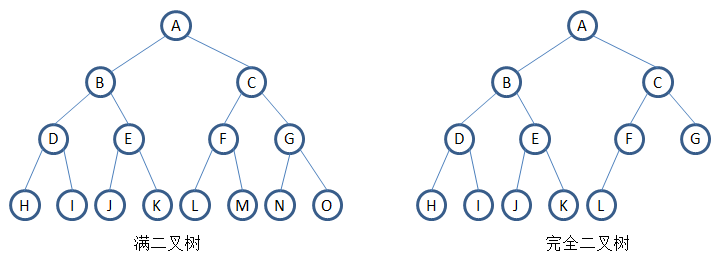
滿二叉樹：一棵深度為k且有2^k - 1個結點的二叉樹稱為滿二叉樹。滿二叉樹上每一層的結點數都是最大節點數。

完全二叉樹：深度為k的，有n個結點的二叉樹，當且僅當其每一個節點都與深度為k的滿二叉樹中自上而下，從左往右編號完全相同的時候，就是完全二叉樹。

注：完全二叉樹是效率很高的資料結構，堆是一種完全二叉樹或者近似完全二叉樹，所以效率極高，像十分常用的排序演算法、Dijkstra演算法、Prim演算法等都要用堆才能優化，二叉排序樹的效率也要藉助平衡性來提高，而平衡性基於完全二叉樹。

二叉樹的特性

（1）二叉樹的第i層上至多有2^i-1個結點（i >= 1）；

（2）深度為k的二叉樹至多有2^k - 1個結點（k >= 1）;

（3）對於任意一棵二叉樹T，如果其終端節點數為n₀，度為2的結點數為n_2，則= _n2 + 1

二叉樹的儲存結構

1、順序儲存結構

有以下3中二叉樹：

按順序儲存的時候，用一組連續的儲存空間從上至下，從左至右，將二叉樹編號 i 的元素儲存在對應1維陣列的下標為 i-1 的位置，對應的儲存結構為：

數組裡元素為0的表示沒有此結點，可以看出：順序儲存結構適合於完全二叉樹，對於非完全二叉樹比較浪費空間，圖(3)只有四個結點對於最壞情況下，需要的空間卻是最多的。

因此，在最壞情況下，一個深度為k且只有k個結點的單支樹（樹中不存在度為2的結點）需要的儲存長度是2^k - 1的一維陣列。

2、鏈式儲存結構

由二叉樹的定義得知：二叉樹的結點由一個數據元素 和 分別指向左子樹、右子樹的兩個分支構成。有時候為了方便，也可以加個雙親結點的指標域，如下圖所示：

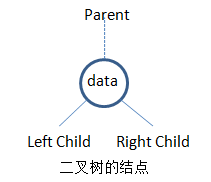
只含有左右子樹的結點 和 含有左右子樹和雙親指標的結點的資料結構：

只含有左右子樹指標的鏈式結構稱為二叉連結串列；含有左右子樹指標和雙親結點指標的鏈式結構稱為三叉連結串列。

如下2種結構的二叉樹：

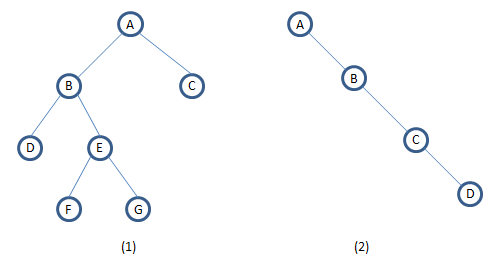對應的鏈式儲存結構為：

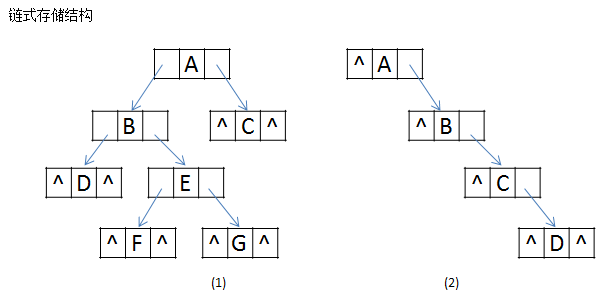
由儲存結構可以得出：有n個結點的二叉連結串列中有n+1個空鏈域。

二叉連結串列和三叉連結串列比較

（1）二叉連結串列少儲存了個parent指標，所以更節省記憶體。

（2）在二叉連結串列中查詢某個元素的雙親結點需要從根節點遍歷查詢，而在三叉連結串列中可以直接通過parent指標拿到。

二叉連結串列和三叉連結串列各有優缺點，具體使用哪種儲存結構需要根據實際情況來決定。

遍歷二叉樹

二叉樹不像線性表結構只需要從前向後遍歷即可訪問每個元素，二叉樹每個結點都可能有兩個分支，所以遍歷方式肯定不像線性表那麼簡單。二叉樹是由若干個結點遞迴構成的，每個結點又由根節點、左子樹和右子樹3個基本單元組成，因此遍歷二叉樹就是依次遍歷這三個部分，每個結點都按某種方法來遍歷，遍歷完所有結點即完成了對二叉樹的遍歷過程。假如限定先左後右，假如一棵二叉樹不為空，則有以下3種方式：

先序遍歷

（1）訪問根節點；

（2）先序遍歷左子樹；

（3）先序遍歷右子樹。

中序遍歷

（1）中序遍歷左子樹；

（2）訪問根節點；

（3）中序遍歷右子樹。

後序遍歷

（1）後序遍歷左子樹；

（2）後序遍歷右子樹；

（3）訪問根節點。

按層次遍歷

從上到下，從左往右，逐層遍歷。

對於二叉樹：

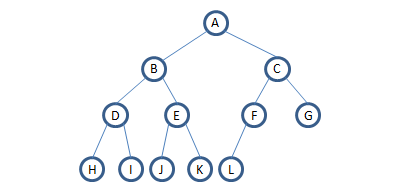
先序遍歷（中左右）：A->B->D->H->I->E->J->k->C->F->L->G
中序遍歷（左中右）：H->D->I->B->J->E->K->A->L->F->C->G
後續遍歷（左右中）：H->I->D->J->K->E->B->L->F->G->C->A

按層遍歷（上->下，左->右）：A->B->C->D->E->F->G->H->I->J->K->L

用遞迴來實現前序、中序、後續遍歷：

//前序 
    private void prePrint(Node node ) {
        if (node == null) return;
        System.out.print(node.getVal());
        prePrint(node.getLeftChild());
        prePrint(node.getRightChild());
    }

    //中序
    private void middlePrint(Node node) {
        if (node == null) return;
        middlePrint(node.getLeftChild());
        System.out.print(node.getVal() + "->");
        middlePrint(node.getRightChild());
    }

    //後續
    private void sufPrint(Node node) {
        if (node == null) return;
        sufPrint(node.getLeftChild());
        sufPrint(node.getRightChild());
        System.out.println(node.getVal());
    }

View Code

線索二叉樹

遍歷二叉樹是以一定規則將二叉樹中結點排列成一個線性序列，不同方法會得到不同序列方式，如先序序列、中序序列和後序序列。這實際上是對一個非線性結構進行線性化的操作，使每個節點（除了第一個和最後一個外）在這些線性序列中有且僅有一個直接前驅和直接後繼。但是，當以二叉連結串列作為儲存結構時候，只能找到左右孩子結點資訊，不能直接得到結點在任一序列中的前驅和後繼資訊，這種資訊只有在遍歷的動態過程中才能得到。如何保持這種線性關係呢？

（1）如果在每個結點上增加兩個指標域prefix 和 suffix，分別表示結點在任一次序遍歷時候的前驅和後繼，雖然可用實現，但是增加的兩個指標域比較耗費空間；

（2）前面我們知道，在有n個結點的二叉連結串列中必定有n+1個空鏈域，如果用空鏈域來儲存結點的前驅和後繼就可以充分利用記憶體空間，所以只需要新增兩個標識位lTag和rTag，用來區分什麼時候指向孩子節點，什麼時候指向前驅（後繼），標識位是布林型別的，比(1)裡的指標更省空間。

如果結點有左子樹，則其lchild指向其左孩子結點，否則讓lchild域指向其前驅；若結點有右子樹，則其rchild指向其右孩子，否則讓rchild指向其後繼。新增兩個標識位，結點結構為：

其中：

       lTag：0   lchild域指示結點的左孩子

               1   lchild域指示結點的前驅

       rTag：0   rchild域指示結點的右孩子

               1   rchild域指示結點的後繼

以這種結點結構構成的二叉連結串列作為二叉樹的儲存結構叫做線索連結串列，其中指向結點前驅和後繼的指標叫做線索，加上線索的二叉樹叫做線索二叉樹，對二叉樹以某種次序遍歷使其變為線索二叉樹的過程叫做線索化。

因為線索化的過程是將二叉連結串列中的空指標改為指向前驅或後繼的線索，而且前驅或後繼資訊是在遍歷過程中才有的，所以線索化即為改變二叉連結串列空指標的過程。

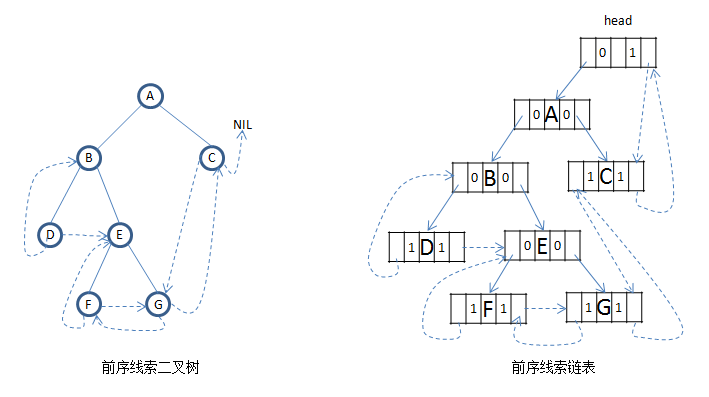
下面分別是前中後序對於的線索二叉樹和線索二叉連結串列，如果給二叉連結串列增加一個head指標，那麼在給定任意一個結點都可以遍歷得到整棵樹：

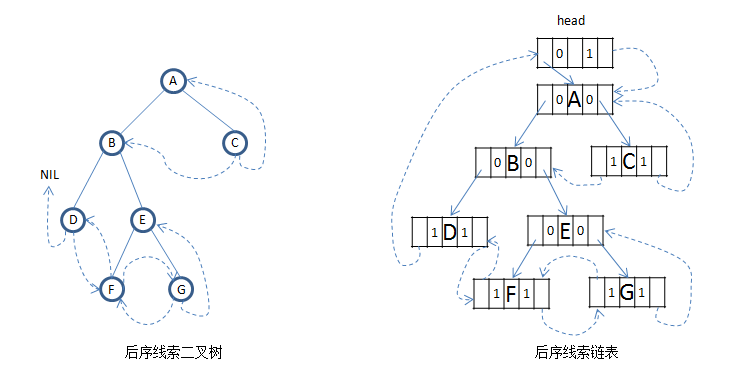
3、樹和森林

樹的3中常用連結串列結構

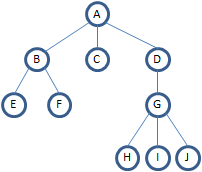
如上圖所示的二叉樹，有以下3中表示方法

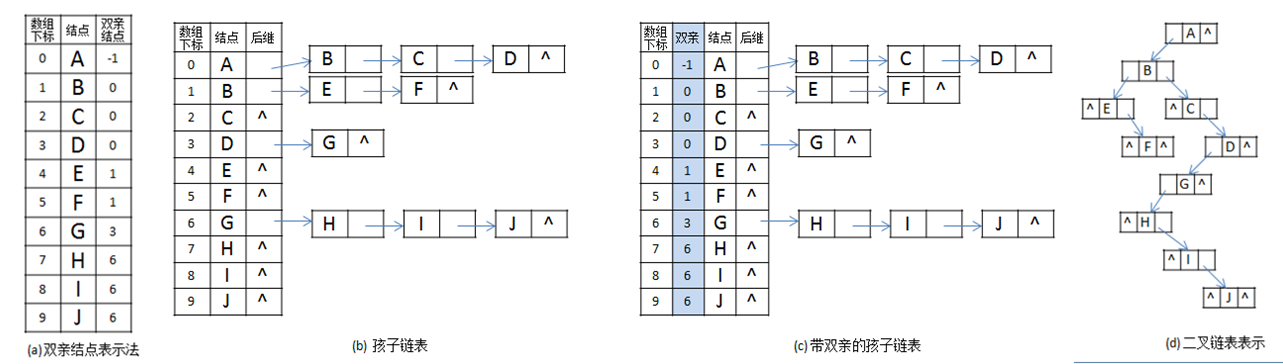
圖（a）雙親表示法

　　假設以一組連續空間儲存樹的結點，儲存結點的同時附加儲存指示雙親的結點在連結串列裡的位置，有圖可知，方便找每個結點的雙親，不太方便找孩子結點（需要遍歷）。

圖（b）、圖（c）孩子表示法

　　圖(b)由每個結點分別指向自己的子樹，構成多重連結串列結構；圖(c)在圖(b)基礎上增加了雙親節點。

圖（d）孩子兄弟表示法

　　又稱為二叉樹表示法或二叉連結串列表示法。連結串列裡每個結點的兩個指標分別指向該節點的第一個孩子結點和下一個兄弟結點。

森林和二叉樹的轉換

前面知道二叉樹可以用二叉連結串列表示，上小結提到樹可以用二叉連結串列表示，所以就可以用二叉連結串列作為儲存媒介將樹與二叉樹對應起來，也就是說對於一棵給定的樹可以找到唯一的一棵二叉樹與之對應，如下圖所示：

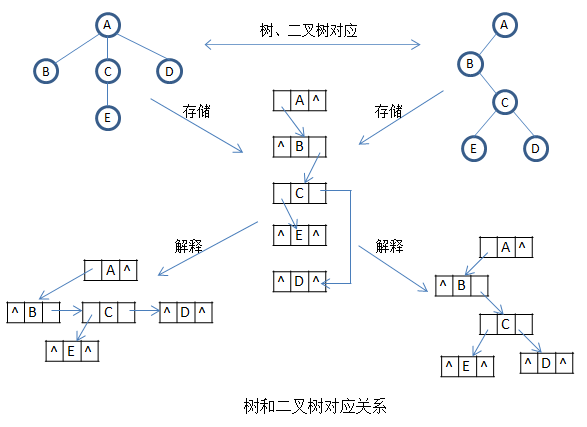
由上節樹的二叉連結串列表示法可以知道：任何一棵樹對應的二叉樹，其右子樹肯定為空（由於根節點肯定沒有兄弟結點）。

如果把第二棵樹根節點看作第一棵樹根節點的兄弟，那麼第二顆樹根節點就是第一棵樹的右子樹，以此類推可以將若干棵樹構成一棵二叉樹（即森林與二叉樹對應關係），如下圖所示：

樹的遍歷

由樹的結構定義可以引出兩種次序遍歷方法：

先根（次序）遍歷樹：先訪問樹的根節點，然後依次先根遍歷根的每顆子樹

後根（次序）遍歷樹：先依次後根遍歷每顆子樹，然後訪問根節點

對這棵樹進行先根遍歷：A B E F C D G

對這棵樹進行後根遍歷：E F B C G D A

森林的遍歷

　　按照森林和樹的定義，可以推出森林的兩種遍歷方法

先序遍歷森林

如果森林非空，可以按下面規則遍歷：

（1）訪問森林中第一棵樹的根節點

（2）先序遍歷第一棵樹中根節點的子樹森林

（3）先序遍歷除去第一棵樹之後的樹構成的森林

中序遍歷森林

如果森林非空，可以按下面規則遍歷：

（1）中序遍歷森林中第一棵樹的根節點的子樹森林

（2）訪問第一棵樹的根節點

（3）中序遍歷除去第一棵樹之後的樹構成的森林

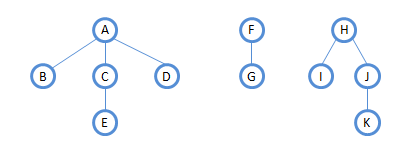
對上圖森林進行遍歷：

先序：A B C E D F G H I J K

中序：B E C D A G F I K J H

由森林轉化成二叉樹得知，對應的二叉樹為

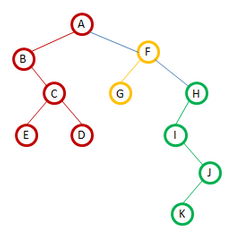
所以森林的先序和中序也就是轉化成二叉樹後，二叉樹的先序和中序遍歷。