來源：http://grunt1223.iteye.com/blog/964564

在工作學習中，我往往感嘆數學奇蹟般的解決一些貌似不可能完成的任務，並且十分希望將這種喜悅分享給大家，就好比說：“老婆，出來看上帝”…… 

隨著資訊爆炸時代的來臨，網際網路上充斥著著大量的近重複資訊，有效地識別它們是一個很有意義的課題。例如，對於搜尋引擎的爬蟲系統來說，收錄重複的網頁是毫無意義的，只會造成儲存和計算資源的浪費；同時，展示重複的資訊對於使用者來說也並不是最好的體驗。造成網頁近重複的可能原因主要包括： 

• 映象網站
• 內容複製
• 嵌入廣告
• 計數改變
• 少量修改

一個簡化的爬蟲系統架構如下圖所示： 




事實上，傳統比較兩個文字相似性的方法，大多是將文字分詞之後，轉化為特徵向量距離的度量，比如常見的歐氏距離、海明距離或者餘弦角度等等。兩兩比較固然能很好地適應，但這種方法的一個最大的缺點就是，無法將其擴充套件到海量資料。例如，試想像Google那種收錄了數以幾十億網際網路資訊的大型搜尋引擎，每天都會通過爬蟲的方式為自己的索引庫新增的數百萬網頁，如果待收錄每一條資料都去和網頁庫裡面的每條記錄算一下餘弦角度，其計算量是相當恐怖的。 

我們考慮採用為每一個web文件通過hash的方式生成一個指紋（fingerprint）。傳統的加密式hash，比如md5，其設計的目的是為了讓整個分佈儘可能地均勻，輸入內容哪怕只有輕微變化，hash就會發生很大地變化。我們理想當中的雜湊函式，需要對幾乎相同的輸入內容，產生相同或者相近的hashcode，換句話說，hashcode的相似程度要能直接反映輸入內容的相似程度。很明顯，前面所說的md5等傳統hash無法滿足我們的需求。 

simhash是locality sensitive hash（區域性敏感雜湊）的一種，最早由Moses Charikar在《similarity estimation techniques from rounding algorithms》一文中提出。Google就是基於此演算法實現網頁檔案查重的。我們假設有以下三段文字： 

• the cat sat on the mat
• the cat sat on a mat
• we all scream for ice cream

使用傳統hash可能會產生如下的結果： 
引用 irb(main):006:0> p1 = 'the cat sat on the mat' irb(main):005:0> p2 = 'the cat sat on a mat' irb(main):007:0> p3 = 'we all scream for ice cream' irb(main):007:0> p1.hash => 415542861 irb(main):007:0> p2.hash => 668720516 irb(main):007:0> p3.hash => 767429688

使用simhash會應該產生類似如下的結果： 
引用 irb(main):003:0> p1.simhash => 851459198 00110010110000000011110001111110 irb(main):004:0> p2.simhash => 847263864 00110010100000000011100001111000 irb(main):002:0> p3.simhash => 984968088 00111010101101010110101110011000

海明距離的定義，為兩個二進位制串中不同位的數量。上述三個文字的simhash結果，其兩兩之間的海明距離為(p1,p2)=4，(p1,p3)=16以及(p2,p3)=12。事實上，這正好符合文字之間的相似度，p1和p2間的相似度要遠大於與p3的。 

如何實現這種hash演算法呢？以上述三個文字為例，整個過程可以分為以下六步： 
1、選擇simhash的位數，請綜合考慮儲存成本以及資料集的大小，比如說32位 
2、將simhash的各位初始化為0 
3、提取原始文字中的特徵，一般採用各種分詞的方式。比如對於"the cat sat on the mat"，採用兩兩分詞的方式得到如下結果：{"th", "he", "e ", " c", "ca", "at", "t ", " s", "sa", " o", "on", "n ", " t", " m", "ma"} 
4、使用傳統的32位hash函式計算各個word的hashcode，比如："th".hash = -502157718 
，"he".hash = -369049682，…… 
5、對各word的hashcode的每一位，如果該位為1，則simhash相應位的值加1；否則減1 
6、對最後得到的32位的simhash，如果該位大於1，則設為1；否則設為0 

整個過程可以參考下圖： 



按照Charikar在論文中闡述的，64位simhash，海明距離在3以內的文字都可以認為是近重複文字。當然，具體數值需要結合具體業務以及經驗值來確定。 

使用上述方法產生的simhash可以用來比較兩個文字之間的相似度。問題是，如何將其擴充套件到海量資料的近重複檢測中去呢？譬如說對於64位的待查詢文字的simhash code來說，如何在海量的樣本庫（>1M）中查詢與其海明距離在3以內的記錄呢？下面在引入simhash的索引結構之前，先提供兩種常規的思路。第一種是方案是查詢待查詢文字的64位simhash code的所有3位以內變化的組合，大約需要四萬多次的查詢，參考下圖： 



另一種方案是預生成庫中所有樣本simhash code的3位變化以內的組合，大約需要佔據4萬多倍的原始空間，參考下圖： 



顯然，上述兩種方法，或者時間複雜度，或者空間複雜度，其一無法滿足實際的需求。我們需要一種方法，其時間複雜度優於前者，空間複雜度優於後者。 

假設我們要尋找海明距離3以內的數值，根據抽屜原理，只要我們將整個64位的二進位制串劃分為4塊，無論如何，匹配的兩個simhash code之間至少有一塊區域是完全相同的，如下圖所示： 



由於我們無法事先得知完全相同的是哪一塊區域，因此我們必須採用儲存多份table的方式。在本例的情況下，我們需要儲存4份table，並將64位的simhash code等分成4份；對於每一個輸入的code，我們通過精確匹配的方式，查詢前16位相同的記錄作為候選記錄，如下圖所示： 



讓我們來總結一下上述演算法的實質： 
1、將64位的二進位制串等分成四塊 
2、調整上述64位二進位制，將任意一塊作為前16位，總共有四種組合，生成四份table 
3、採用精確匹配的方式查詢前16位 
4、如果樣本庫中存有2^34（差不多10億）的雜湊指紋，則每個table返回2^(34-16)=262144個候選結果，大大減少了海明距離的計算成本 

我們可以將這種方法拓展成多種配置，不過，請記住，table的數量與每個table返回的結果呈此消彼長的關係，也就是說，時間效率與空間效率不可兼得，參看下圖： 



事實上，這就是Google每天所做的，用來識別獲取的網頁是否與它龐大的、數以十億計的網頁庫是否重複。另外，simhash還可以用於資訊聚類、檔案壓縮等。 

也許，讀到這裡，你已經感受到數學的魅力了。

前幾天去吃葫蘆頭的路上，大飛哥給詳細的講解了他在比較文字相似度實驗時對Google的simhash方法高效的驚歎，回來特意去找了原文去拜讀。

Simhash

傳統IR領域內文字相似度比較所採用的經典方法是文字相似度的向量夾角餘弦，其主要思想是根據一個文章中出現詞的詞頻構成一個向量，然後計算兩篇文章對應向量的向量夾角。但由於有可能一個文章的特徵向量詞特別多導致整個向量維度很高，使得計算的代價太大，對於Google這種處理萬億級別的網頁的搜尋引擎而言是不可接受的，simhash演算法的主要思想是降維，將高維的特徵向量對映成一個f-bit的指紋(fingerprint)，通過比較兩篇文章的f-bit指紋的Hamming Distance來確定文章是否重複或者高度近似。

simhash演算法很精巧，但卻十分容易理解和實現，具體的simhash過程如下：

1. 首先基於傳統的IR方法，將文章轉換為一組加權的特徵值構成的向量。

2.初始化一個f維的向量V，其中每一個元素初始值為0。

3.對於文章的特徵向量集中的每一個特徵，做如下計算：

利用傳統的hash演算法對映到一個f-bit的簽名。對於這個f- bit的簽名，如果簽名的第i位上為1，則對向量V中第i維加上這個特徵的權值，否則對向量的第i維減去該特徵的權值。

4.對整個特徵向量集合迭代上述運算後，根據V中每一維向量的符號來確定生成的f-bit指紋的值，如果V的第i維為正數，則生成f-bit指紋的第i維為1，否則為0。

simhash和普通hash最大的不同在於傳統的hash函式雖然也可以用於對映來比較文字的重複，但是對於可能差距只有一個位元組的文件也會對映成兩個完全不同的雜湊結果，而simhash對相似的文字的雜湊對映結果也相似。Google的論文中取了f=64，即將整個網頁的加權特徵集合對映到一個64-bit的fingerprint上。

比起simhash，整片文章中Google所採用的查詢與給定f-bit的fingerprint的海明距離(Hamming Distance)小於k的演算法相對還稍微難理解點。

fingerprint的Hamming Distance

問題：一個80億的64-bit指紋組成的集合Q，對於一個給定64-bit的指紋F，如何在a few millionseconds中找到Q中和f至多隻有k(k=3)位差別的指紋。

思想：1. 對於一個具有2^d個記錄的集合，只需要考慮d-bit hash。2. 選取一個d’使得|d’-d|十分小，因此如果兩fingerprint在d’-bits上都相同，那麼在d-bits也很可能相同。然後在這些d-bit match的結果中尋找整個f-bit的Hamming Distance小於k的fingerprint。 簡單的說，就是利用fingerprint少量特徵位數比較從而首先縮小範圍，然後再去確定是否差異小於k個bit。

演算法：

1. 首先對於集合Q構建多個表T1，T2…Tt，每一個表都是採用對應的置換函式π(i)將64-bit的fingerprint中的某p(i)位序列置換換到整個序列的最前面。即每個表儲存都是整個Q的fingerprint的複製置換。

2.對於給定的F，在每個Ti中進行匹配，尋找所有前pi位與F經過π(i)置換後的前pi位相同的fingerprint。

3.對於所有在上一步中匹配到的置換後的fingerprint，計算其是否與π(i)(F)至多有k-bit不同。

演算法的重點在於對於集合Q的分表以及每個表所對應的置換函式，假設對於64-bit的fingerprint，k=3，儲存16個table，劃分參考下圖:

將64-bit按照16位劃分為4個區間，每個區間剩餘的48-bit再按照每個12-bit劃分為4個區間，因此總共16個table並行查詢，即使三個不同的k-bit落在A、B、C、D中三個不同的區塊，此劃分方法也不會導致遺漏。

以上方法是對於online的query，即一個給定的F在集合中查詢相似的fingerprint。如果爬蟲每天爬取了100w個網頁，快速的查詢這些新抓取的網頁是否在原集合中有Near-duplication，對於這種batch-query的情況，Map-Reduce就發揮它的威力了。

不同的是，在batch-query的處理中，是對待查集合B(1M個fingerprint)進行復制置換構建Table而非8B的目標集合，而在每一個chunkserver上對Fi(F為整個8B的fingerprint)在整個Table(B)中進行探測，每一個chunkserver上的的該Map過程輸出該Fi中與整個B的near-duplicates，Reduces過程則將所有的結果收集、去重、然後輸出為一個sorted file。

Haffman編碼壓縮

上述的查詢過程，特別是針對online-version的演算法，可以看出需要對8B的fingerprint進行多表複製和構建，其佔據的容量是非常大的，不過由於構建的每一個置換Table都是sorted的，因此可以利用每一個fingerprint與其前一個的開始不同的bit-position h(h∈[0,f-1]) 來進行資料壓縮，即如果前一個編碼是11011011，而自身是11011001，則後一個可以編碼為(6)1，即h=6，其中6表示從第6位(從0開始編號)開始和上一個fingerprint不相同(上一個為1，這個必然為0)，然後再儲存不相同位置右側的編碼，依次生成整個table。

Google首先計算整個排序的fingerprint表中h的分佈情況，即不同的h出現次數，依據此對[0,f-1]上出現的h建立Haffman code，再根據上述規則生成table（例如上面的6就表示成對應的Haffman code）。其中table分為多個block，每一個block中的第一個fingerprint儲存原資料，後面的依次按照編碼生成。

將每一個block中所對應的最後一個fingerprint儲存在記憶體中，因此在比對的時候就可以直接根據記憶體中的fingerprint來確定是哪一個block需要被decompress進行比較。

8B個64-bit的fingerprint原佔據空間大約為64GB，利用上述Haffman code壓縮後幾乎會減少一般，而記憶體中又只對每一個block儲存了一個fingerprint。

每次看Google的論文都會讓人眼前一亮，而且與很多(特別是國內)的論文是對未來進行設想不同，Google的東西都是已經運行了2，3年了再到WWW，OSDI這種頂級會議上灌個水。再次各種羨慕能去這個Dream Company工作的人，你們懂得。

參考:

有1億個不重複的64位的01字串，任意給出一個64位的01字串f，如何快速從中找出與f漢明距離小於3的字串？

大規模網頁的近似查重

WWW上存在大量內容近似相同的網頁，對搜尋引擎而言，去除近似相同的網頁可以提高檢索效率、降低儲存開銷。

當爬蟲在抓取網頁時必須很快能在海量文字集中快速找出是否有重複的網頁。

論文主要2個貢獻：

1.      展示了simhash可以用以海量文字查重

2.      提出了一個在實際應用中可行的演算法。

兩篇文字相似度普遍的定義是比較向量化之後兩個詞袋中詞的交集程度，有cosine,jaccard等等

如果直接使用這種計算方式，時間空間複雜度都太高，因此有了simhash這種降維技術，

但是如何從傳統的向量相似度能用simhash來近似，論文沒提，應該是有很長一段推導要走的。

Simhash演算法

一篇文字提取出內容以後，經過基本的預處理，比如去除停詞，詞根還原，甚至chunking，最後可以得到一個向量。

對每一個term進行hash演算法轉換，得到長度f位的hash碼，每一位上1-0值進行正負權值轉換，例如f1位是1時，權值設為 +weight, fk位為0時，權值設為-weight。

講文字中所有的term轉換出的weight向量按f對應位累加最後得到一個f位的權值陣列，位為正的置1，位為負的置0，那麼文字就轉變成一個f位的新1-0陣列，也就是一個新的hash碼。

Simhash具有兩個“衝突的性質”：

1.      它是一個hash方法

2.      相似的文字具有相似的hash值，如果兩個文字的simhash越接近，也就是漢明距離越小，文字就越相似。

因此海量文字中查重的任務轉換位如何在海量simhash中快速確定是否存在漢明距離小的指紋。

也就是：在n個f-bit的指紋中，查詢漢明距離小於k的指紋。

在文章的實驗中（見最後），simhash採用64位的雜湊函式。在80億網頁規模下漢明距離=3剛好合適。

因此任務的f-bit=64 , k=3 , n= 8*10^11

任務清晰，首先看一下兩種很直觀的方法：

1.      對輸入指紋，枚舉出所有漢明距離小於3的simhash指紋，對每個指紋在80億排序指紋中查詢。

（這種方法需要進行C（64，3）=41664次的simhash指紋，再為每個進行一次查詢）

2.     輸入指紋不變，對應集合相應位置變。也就是集合上任意3位組合的位置進行變化，實際上就是提前準備41664個排序可能，需要龐大的空間。輸入在這群集合並行去搜....

提出的方法介於兩者之間，合理的空間和時間的折中。

•        假設我們有一個已經排序的容量為2^d，f-bit指紋集。看每個指紋的高d位。該高低位具有以下性質：儘管有很多的2^d位組合存在，但高d位中有隻有少量重複的。

•        現在找一個接近於d的數字d’，由於整個表是排好序的，所以一趟搜尋就能找出高d’位與目標指紋F相同的指紋集合f’。因為d’和d很接近，所以找出的集合f’也不會很大。

•        最後在集合f’中查詢和F之間海明距離為k的指紋也就很快了。

•        總的思想：先要把檢索的集合縮小，然後在小集合中檢索f-d’位的海明距離

 要是一時半會看不懂，那就從新回顧一下那兩種極端的辦法：

方法2，前61位上精確匹配，後面就不需要比較了

方法1，前0位上精確匹配，那就要在後面，也就是所有，上比較

 那麼折中的想法是 前d- bits相同，留下3bit在(64-d)bit小範圍搜尋，可行否?

d-bits的表示範圍有2^d，總量N個指紋，平均 每個表示後面只有N/(2^d)個快速定位到字首是d的位置以後，直接比較N/(2^k)個指紋。

 如此只能保證前d位精確的那部分N/(2^d)指紋沒有遺漏漢明距離>3的因此要保證64bits上所有部分都安全，全部才沒有遺漏。方法2其實就是把所有的d=61 部分(也就是64選61)都包含了。

按照例子，80億網頁有2^34個，那麼理論上34位就能表示完80億不重複的指紋。

我們假設最前的34位的表示完了80億指紋，假設指紋在前30位是一樣的，那麼後面4位還可以表示2⁴個，只需要逐一比較這16個指紋是否於待測指紋漢明距離小於3。

假設：對任意34位中的30位都可以這麼做。

因此在一次完整的查詢中，限定前q位精確匹配（假設這些指紋已經是q位有序的，可以採用二分查詢，如果指紋量非常大，且分佈均勻，甚至可以採用內插搜尋），之後的2^d-q個指紋剩下64-q位需要比較漢明距離小於3。

於是問題就轉變為如何切割64位的q。

將64位平分成若干份，例如4份ABCD，每份16位。

假設這些指紋已經按A部分排序好了，我們先按A的16位精確匹配到一個區間，這個區間的後BCD位檢查漢明距離是否小於3。

同樣的假設，其次我們按B的16位精確匹配到另一個區間，這個區間的所有指紋需要在ACD位上比較漢明距離是否小於3。

同理還有C和D

所以這裡我們需要將全部的指紋T複製4份，T1 T2 T3 T4， T1按A排序，T2按B排序… 4份可以並行進行查詢，最後把結果合併。這樣即使最壞的情況：3個位分別落在其中3個區域ABC,ACD,BCD,ABD…都不會被漏掉。

只精確匹配16位，還需要逐一比較的指紋量依然龐大，可能達到2^d-16個，我們也可以精確匹配更多的。

例如：將64位平分成4份ABCD，每份16位，在BCD的48位上，我們再分成4份，WXZY，每份12位，漢明距離的3位可以散落在任意三塊，那麼A與WXZY任意一份合起來做精確的28位…剩下3份用來檢查漢明距離。同理B，C，D也可以這樣，那麼T需要複製16次，ABCD與WXYZ的組合做精確匹配，每次精確匹配後還需要逐一比較的個數降低到2^d-28個。不同的組合方式也就是時間和空間上的權衡。

最壞情況是其中3份可能有1位漢明距離差異為1。

演算法的描述如下：

1）先複製原表T為Tt份：T1,T2,….Tt

2）每個Ti都關聯一個pi和一個πi，其中pi是一個整數,πi是一個置換函式，負責把pi個bit位換到高位上。

3）應用置換函式πi到相應的Ti表上，然後對Ti進行排序

4）然後對每一個Ti和要匹配的指紋F、海明距離k做如下運算：

a)      然後使用F’的高pi位檢索，找出Ti中高pi位相同的集合

b)     在檢索出的集合中比較f-pi位，找出海明距離小於等於k的指紋

5）最後合併所有Ti中檢索出的結果

由於文字已經壓縮成8個位元組了，因此其實Simhash近似查重精度並不高：

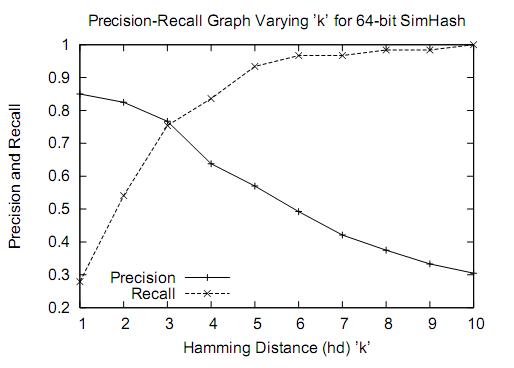
simhash演算法原理及實現

simhash是google用來處理海量文字去重的演算法。 google出品，你懂的。 simhash最牛逼的一點就是將一個文件，最後轉換成一個64位的位元組，暫且稱之為特徵字，然後判斷重複只需要判斷他們的特徵字的距離是不是<n（根據經驗這個n一般取值為3），就可以判斷兩個文件是否相似。

原理

simhash值的生成圖解如下：

大概花三分鐘看懂這個圖就差不多怎麼實現這個simhash演算法了。特別簡單。谷歌出品嘛，簡單實用。

演算法過程大概如下：

1. 將Doc進行關鍵詞抽取(其中包括分詞和計算權重)，抽取出n個(關鍵詞，權重)對， 即圖中的(feature, weight)們。 記為 feature_weight_pairs = [fw1, fw2 ... fwn]，其中 fwn = (feature_n, weight_n)。
2. hash_weight_pairs = [ (hash(feature), weight) for feature, weight in feature_weight_pairs ] 生成圖中的(hash,weight)們, 此時假設hash生成的位數bits_count = 6（如圖）;
3. 然後對 hash_weight_pairs 進行位的縱向累加，如果該位是1，則+weight,如果是0，則-weight，最後生成bits_count個數字，如圖所示是[13, 108, -22, -5, -32, 55], 這裡產生的值和hash函式所用的演算法相關。
4. [13,108,-22,-5,-32,55] -> 110001這個就很簡單啦，正1負0。

到此，如何從一個doc到一個simhash值的過程已經講明白了。 但是還有一個重要的部分沒講，

simhash值的海明距離計算

二進位制串A 和 二進位制串B 的海明距離 就是 A xor B 後二進位制中1的個數。

舉例如下：

A = 100111;
B = 101010;
hamming_distance(A, B) = count_1(A xor B) = count_1(001101) = 3;

當我們算出所有doc的simhash值之後，需要計算doc A和doc B之間是否相似的條件是：

A和B的海明距離是否小於等於n，這個n值根據經驗一般取值為3,

simhash本質上是區域性敏感性的hash，和md5之類的不一樣。 正因為它的區域性敏感性，所以我們可以使用海明距離來衡量simhash值的相似度。

高效計算二進位制序列中1的個數

/* src/Simhasher.hpp */
bool isEqual(uint64_t lhs, uint64_t rhs, unsigned short n = 3)
{
    unsigned short cnt = 0;
    lhs ^= rhs;
    while(lhs && cnt <= n)
    {
        lhs &= lhs - 1;
        cnt++;
    }
    if(cnt <= n)
    {
        return true;
    }
    return false;
}

由上式這個函式來計算的話，時間複雜度是 O(n); 這裡的n預設取值為3。由此可見還是蠻高效的。

simhash實現的工程專案

主要是針對中文文件，也就是此專案進行simhash之前同時還進行了分詞和關鍵詞的抽取。

對比其他演算法

百度的去重演算法

百度的去重演算法最簡單，就是直接找出此文章的最長的n句話，做一遍hash簽名。n一般取3。 工程實現巨簡單，據說準確率和召回率都能到達80%以上。

shingle演算法

shingle原理略複雜，不細說。 shingle演算法我認為過於學院派，對於工程實現不夠友好，速度太慢，基本上無法處理海量資料。

其他演算法

具體看微博上的討論

參考

[python] view plain