1、k近鄰演算法

1.1 KNN基本思想

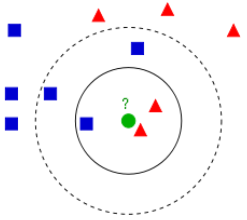
k近鄰法是基本且簡單的分類與迴歸方法，即對於輸入例項，依據給定的距離度量方式（歐式距離），以及選擇合適的k值（交叉驗證），在樣本集中找到最近鄰新例項的k個樣例，通過k個最近鄰樣例的類別表決出新例項的類別（多數表決）。當k為1時，稱為最近鄰。

K近鄰法是基於樣本集對特徵空間的一個劃分，沒有顯式的學習過程。k近鄰模型由 距離度量、k值選擇和分類決策規則決定。

1.2 距離距離——p範數

特徵空間中兩個特徵向量$\bm x_i=(x_i^1, x_i^2, \cdots, x_i^n)$

當$p=1$時，稱為曼哈頓距離；當$p=2$時，稱為 歐式距離

1.3 選擇k值——交叉驗證取最小

k的選擇反映了訓練誤差（近似誤差）與測試誤差（估計誤差）的權衡，即：

• 若 k取較小值（模型複雜），預測例項較依賴於近鄰樣本，樣本整體利用率低，模型對噪聲資料敏感，且可能出現訓練誤差小（過擬合）、測試誤差大的情況；
• 若 k值較大（模型簡單），預測例項可利用較多的樣本資訊，模型抗干擾性強，但計算複雜，且可能出現訓練誤差大（欠擬合）、測試誤差小的情況。

實際運用中，一般通過 交叉驗證選取較小的最優k值。

1.4 分類決策——多數表決

給定例項$\bm x \in \mathcal X$，其最近鄰的$k$個樣本構成集合$N_{}$

最小化誤分類率，等價於最小化經驗風險$\sum\limits_{\bm x_i \in N_k(\bm x)}I(y_i \neq c)$，故 多數表決規則等價於經驗風險最小化。

1.4 k近鄰評價

當不同類別的樣本容量不一致時，模型傾向於樣本容量大的類別，可通過將類別附加權值改進模型；
佔用儲存空間，計算量大（可優化改進，如kd樹儲存結構）；

2、優化搜尋之kd樹

2.1 什麼是kd樹？

實現KNN演算法時，主要考慮的問題是如何在訓練樣本集中快速k近鄰搜尋。最簡單的想法是，使用線性掃描的方式，即計算所有樣本點與輸入例項的距離，再取k個距離最小的點作為k近鄰點。當訓練集很大時，這種方法計算非常耗時。另一種想法是，構建資料索引，即通過構建樹對輸入空間進行劃分，kd樹就是此種實現。

kd樹（k-dimension tree，k是指特徵向量的維數），是一種儲存k維空間中資料的平衡二叉樹型結構，主要用於 範圍搜尋和最近鄰搜尋。kd樹實質是一種空間劃分樹，其每個節點對應一個k維的點，每個非葉節點相當於一個分割超平面，將其所在區域劃分為兩個子區域。

kd樹的結構可使得每次在區域性空間中搜尋目標資料，減少了不必要的資料搜尋，從而加快了搜尋速度。

2.2 如何構建kd樹？

構建kd樹的過程，是不斷地選擇垂直於座標軸（切分軸）的超平面將樣本集所在的k維空間二分，生成一系列不重疊的k維超矩形區域。

選擇切分軸
有多種方法可以選擇切分軸超平面，如隨著樹的深度輪流選擇各軸、每次選擇數值方差最大的軸等。

選擇切分點
一般使用中位數作為切分點，可保證切分後得到的左右子樹深度差不超過1，所得二叉樹為平衡二叉樹。

構建過程
輸入資料集$T = \{\bm x_1, \cdots, \bm x_N\}$，其中$\bm x_i=(x_i^1, \cdots, x_i^k)$，具體步驟如下：

• 構建根節點，根節點對應於包含$T$的k維空間的超矩形區域。選取$x^1$為切分軸、$T$中所有點$x^1$座標的中位數為切分點，使用過切分點且與垂直於切分軸的超平面，將根節點對應的超矩形區域切分為兩個子區域，並對應於其左右子節點。其中，左節點區域各點的$x^1$座標不大於切分點，右節點區域各點的$x^1$座標大小於切分點，並將切分點儲存在根節點。

• 對子節點重複步驟$I$，即對於深度為$j$的節點$j_i$，選擇$x^l$為切分軸、$j_i$包含的區域中所有點$x^l$座標的中位數為切分點，其中$l=(j+1) \mod k$，將$j_i$對應的區域劃分為兩個子區域，並對應其左右子節點，直至兩個子區域沒有例項為止。

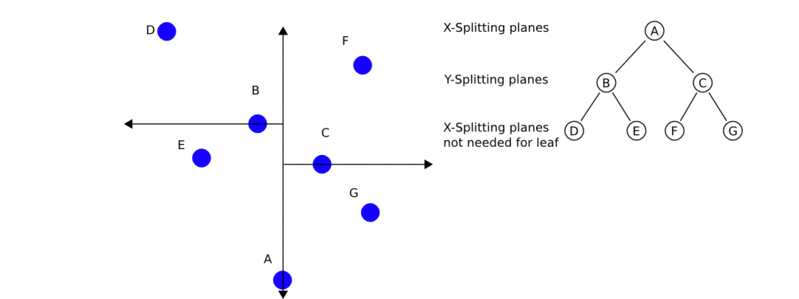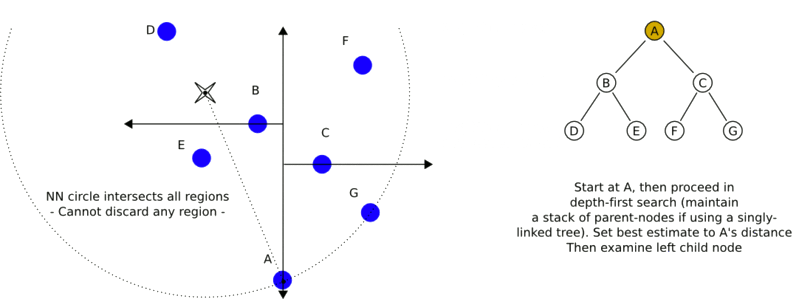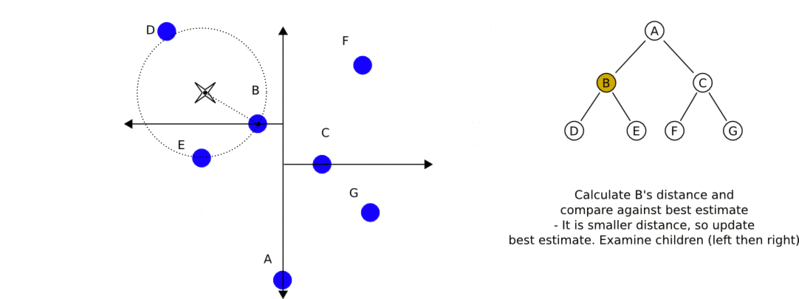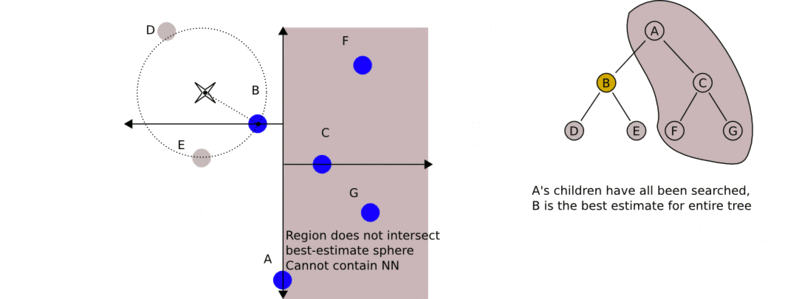
對於二維空間中的資料集，$T=\{(2, 3), (5, 4), (9, 6), (4, 7), (8, 1), (7, 2)\}$，形成的kd樹如下：

   

2.3 如何在kd樹中搜索輸入例項的k近鄰？

利用kd樹搜尋最近鄰樣本，可省去對大部分資料的搜尋，從而減少計算量。當資料隨機分佈時，搜尋最近鄰的時間複雜度為$O(\log N)$，$N$為樣本集容量，當空間維數接近$N$時，效率迅速下降。如下圖3為搜尋過程動態效果圖。

最近鄰搜尋
給定一個輸入例項，首先找到包含輸入例項的葉節點。然後從該葉節點出發，依次回退到父節點。不斷查詢與輸入例項最近鄰的節點，當不存在距離更小的節點時終止搜尋《統計學習方法》。
輸入例項與其最近鄰樣本點形成的超球體的內部一定沒有其他樣本點。 基於這種性質，最近鄰搜尋演算法如下：

1. 從根節點出發，找到包含輸入例項的葉節點，即若輸入例項當前維的座標小於切分點的座標，移動到左子節點，否則移動到右子節點，直到到達葉節點未知，並將當前葉節點作為“當前最近點”；
2. 遞迴地向上回退，對每個節點執行以下操作：
   a. 若該節點儲存的例項比"當前最近點"距離輸入例項更近，則將該例項作為“當前最近點”；
   b. “當前最近點”一定存在於該節點一個子節點對應的區域，檢查該子節點的兄弟節點對應區域是否有更近的點。即若“當前最近點”與輸入例項形成的超球體與"當前最近點"的父節點的分割超平面相交，則"當前最近點"的兄弟節點可能含有更近的點，此時將該兄弟節點作為根節點一樣，執行步驟1。若不相交，則向上回退。
3. 當回退到根節點時，搜尋結束。最後的“當前最近點”，即為輸入例項的最近鄰點。

k近鄰搜尋
《統計學習方法》中未介紹k近鄰的搜尋演算法，通過查詢其它資料，整理了演算法實現思想。
最近鄰的搜尋演算法是首先找到葉節點，再依次向上回退，直至到達根節點。本文章中的k近鄰的搜尋演算法與其相反，是從根節點開始依次向下查詢，直至到達葉節點。演算法實現如下：

• 首先構建空的最大堆（列表），從根節點出發，計算當前節點與輸入例項的距離，若最大堆元素小於k個，則將距離插入最大堆中，否則比較該距離是否小於堆頂距離值，若小於，則使用該距離替換堆頂元素；
• 遞迴的遍歷kd樹中的節點，通過如下方式控制進入分支：
  • 若堆中元素小於k個或該節點中的樣本點與輸入例項形成的超球體包含堆頂樣本點，則進入左右子節點搜尋；
  • 否則，若輸入例項當前維的座標小於該節點當前維的座標，則進入左子節點搜尋；
  • 否則，進入右子節點搜尋；
• 當到達葉節點時，搜尋結束。最後最大堆中的k個節點，即為輸入例項的k近鄰點。

3、python實現KD樹、KNN演算法

3.1 python程式碼

# -*- coding: utf-8 -*-l
import random
from copy import deepcopy
from time import time

import numpy as np
from numpy.linalg import norm

from collections import Counter

Counter([0, 1, 1, 2, 2, 3, 3, 4, 3, 3]).most_common(1)


def partition_sort(arr, k, key=lambda x: x):
    """
    以樞紐(位置k)為中心將陣列劃分為兩部分, 樞紐左側的元素不大於樞紐右側的元素

    :param arr: 待劃分陣列
    :param p: 樞紐前部元素個數
    :param key: 比較方式
    :return: None
    """
    start, end = 0, len(arr) - 1
    assert 0 <= k <= end
    while True:
        i, j, pivot = start, end, deepcopy(arr[start])
        while i < j:
            # 從右向左查詢較小元素
            while i < j and key(pivot) <= key(arr[j]):
                j -= 1
            if i == j: break
            arr[i] = arr[j]
            i += 1
            # 從左向右查詢較大元素
            while i < j and key(arr[i]) <= key(pivot):
                i += 1
            if i == j: break
            arr[j] = arr[i]
            j -= 1
        arr[i] = pivot

        if i == k:
            return
        elif i < k:
            start = i + 1
        else:
            end = i - 1


def max_heapreplace(heap, new_node, key=lambda x: x[1]):
    """
    大根堆替換堆頂元素

    :param heap: 大根堆/列表
    :param new_node: 新節點
    :return: None
    """
    heap[0] = new_node
    root, child = 0, 1
    end = len(heap) - 1
    while child <= end:
        if child < end and key(heap[child]) < key(heap[child + 1]):
            child += 1
        if key(heap[child]) <= key(new_node):
            break
        heap[root] = heap[child]
        root, child = child, 2 * child + 1
    heap[root] = new_node


def max_heappush(heap, new_node, key=lambda x: x[1]):
    """
    大根堆插入元素

    :param heap: 大根堆/列表
    :param new_node: 新節點
    :return: None
    """
    heap.append(new_node)
    pos = len(heap) - 1
    while 0 < pos:
        parent_pos = pos - 1 >> 1
        if key(new_node) <= key(heap[parent_pos]):
            break
        heap[pos] = heap[parent_pos]
        pos = parent_pos
    heap[pos] = new_node


class KDNode(object):
    """kd樹節點"""

    def __init__(self, data=None, label=None, left=None, right=None, axis=None, parent=None):
        """
        建構函式

        :param data: 資料
        :param label: 資料標籤
        :param left: 左孩子節點
        :param right: 右孩子節點
        :param axis: 分割軸
        :param parent: 父節點
        """
        self.data = data
        self.label = label
        self.left = left
        self.right = right
        self.axis = axis
        self.parent = parent


class KDTree(object):
    """kd樹"""

    def __init__(self, X, y=None):
        """
        建構函式

        :param X: 輸入特徵集, n_samples*n_features
        :param y: 輸入標籤集, 1*n_sample