問題描述　　數軸上有一條長度為L（L為偶數)的線段，左端點在原點，右端點在座標L處。有n個不計體積的小球線上段上，開始時所有的小球都處在偶數座標上，速度方向向右，速度大小為1單位長度每秒。
　　當小球到達線段的端點（左端點或右端點）的時候，會立即向相反的方向移動，速度大小仍然為原來大小。
　　當兩個小球撞到一起的時候，兩個小球會分別向與自己原來移動的方向相反的方向，以原來的速度大小繼續移動。
　　現在，告訴你線段的長度L，小球數量n，以及n個小球的初始位置，請你計算t秒之後，各個小球的位置。提示　　因為所有小球的初始位置都為偶數，而且線段的長度為偶數，可以證明，不會有三個小球同時相撞，小球到達線段端點以及小球之間的碰撞時刻均為整數。
　　同時也可以證明兩個小球發生碰撞的位置一定是整數（但不一定是偶數）。輸入格式　　輸入的第一行包含三個整數n, L, t，用空格分隔，分別表示小球的個數、線段長度和你需要計算t秒之後小球的位置。
　　第二行包含n個整數a1, a2, …, an，用空格分隔，表示初始時刻n個小球的位置。輸出格式　　輸出一行包含n個整數，用空格分隔，第i個整數代表初始時刻位於ai的小球，在t秒之後的位置。樣例輸入3 10 5
4 6 8樣例輸出7 9 9樣例說明　　初始時，三個小球的位置分別為4, 6, 8。

　　一秒後，三個小球的位置分別為5, 7, 9。

　　兩秒後，第三個小球碰到牆壁，速度反向，三個小球位置分別為6, 8, 10。

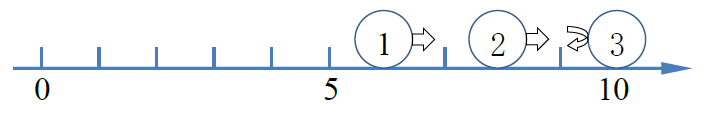
　　三秒後，第二個小球與第三個小球在位置9發生碰撞，速度反向（注意碰撞位置不一定為偶數），三個小球位置分別為7, 9, 9。

　　四秒後，第一個小球與第二個小球在位置8發生碰撞，速度反向，第三個小球碰到牆壁，速度反向，三個小球位置分別為8, 8, 10。


　　五秒後，三個小球的位置分別為7, 9, 9。
樣例輸入10 22 30
14 12 16 6 10 2 8 20 18 4樣例輸出6 6 8 2 4 0 4 12 10 2資料規模和約定　　對於所有評測用例，1 ≤ n ≤ 100，1 ≤ t ≤ 100，2 ≤ L ≤ 1000，0 < ai < L。L為偶數。
　　保證所有小球的初始位置互不相同且均為偶數。

#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
int main()
{
		int n,L,t;	
		int s[105];//={14 ,12, 16, 6, 10, 2, 8, 20, 18, 4};
		int p[105];//={1,1,1,1,1,1,1,1,1,1};
		cin>>n>>L>>t;
		for(int i=0;i<n;i++)
		{
			cin>>p[i];
			if(p[i] == L)
				p[i] = -p[i];
			s[i]=1;
		}	
		for(int i=0;i<t;i++)
		{	
			for(int j=0;j<n;j++) 
				p[j] +=1;		
			for(int j=0;j<n;j++)
			{
				for(int k=0;k<n;k++)
				{	
					if( p[j] == -p[k] || abs(p[j]) == L)
					{
						s[j] = -1;
					}
				}
			}
			for(int j=0;j<n;j++)
			{
				p[j] = p[j]*s[j];
				s[j]=1;
			}
/*			for(int j=0;j<n;j++)
			{
				cout<<p[j]<<" ";
			}
			printf("\n");
*/			
		}    		
		for(int j=0;j<n;j++)
			cout<<abs(p[j])<<" ";	
		return 0;
}