題目要求

Linked List Cycle

Given a linked list, determine if it has a cycle in it.

Follow up: Can you solve it without using extra space?

如何判斷一個單鏈表中有環？

Linked List Cycle II

Given a linked list, return the node where the cycle begins. If there is no cycle, return null.

Follow up: Can you solve it without using extra space?

如何找到環的第一個節點？

分析

 一開始使用了複雜度O(n^2)的方法，使用兩個指標a, b。a從表頭開始一步一步往前走，遇到null則說明沒有環，返回false；a每走一步，b從頭開始走，如果遇到b==a.next，則說明有環true，如果遇到b==a，則說明暫時沒有環，繼續迴圈。

後來找到了複雜度O(n)的方法，使用兩個指標slow,fast。兩個指標都從表頭開始走，slow每次走一步，fast每次走兩步，如果fast遇到null，則說明沒有環，返回false；如果slow==fast，說明有環，並且此時fast超了slow一圈，返回true。

為什麼有環的情況下二者一定會相遇呢？因為fast先進入環，在slow進入之後，如果把slow看作在前面，fast在後面每次迴圈都向slow靠近1，所以一定會相遇，而不會出現fast直接跳過slow的情況。

擴充套件問題

在網上搜集了一下這個問題相關的一些問題，思路開闊了不少，總結如下：

1. 環的長度是多少？

2. 如何找到環中第一個節點（即Linked List Cycle II）？

3. 如何將有環的連結串列變成單鏈表（解除環）？

4. 如何判斷兩個單鏈表是否有交點？如何找到第一個相交的節點？

首先我們看下面這張圖：

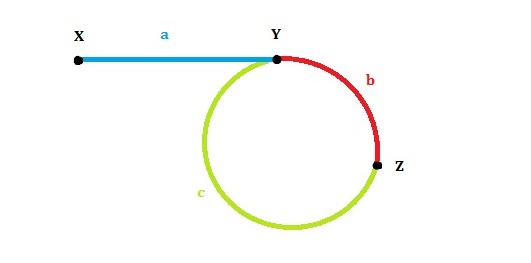
設：連結串列頭是X，環的第一個節點是Y，slow和fast第一次的交點是Z。各段的長度分別是a,b,c，如圖所示。環的長度是L。slow和fast的速度分別是qs,qf。

下面我們來挨個問題分析。

1. 方法一（網上都是這個答案）：

第一次相遇後，讓slow,fast繼續走，記錄到下次相遇時迴圈了幾次。因為當fast第二次到達Z點時，fast走了一圈，slow走了半圈，而當fast第三次到達Z點時，fast走了兩圈，slow走了一圈，正好還在Z點相遇。

方法二：

第一次相遇後，讓fast停著不走了，slow繼續走，記錄到下次相遇時迴圈了幾次。

方法三（最簡單）：

第一次相遇時slow走過的距離：a+b，fast走過的距離：a+b+c+b。

因為fast的速度是slow的兩倍，所以fast走的距離是slow的兩倍，有 2(a+b) = a+b+c+b，可以得到a=c（這個結論很重要！）。

我們發現L=b+c=a+b，也就是說，從一開始到二者第一次相遇，迴圈的次數就等於環的長度。

2. 我們已經得到了結論a=c，那麼讓兩個指標分別從X和Z開始走，每次走一步，那麼正好會在Y相遇！也就是環的第一個節點。

3. 在上一個問題的最後，將c段中Y點之前的那個節點與Y的連結切斷即可。

4. 如何判斷兩個單鏈表是否有交點？先判斷兩個連結串列是否有環，如果一個有環一個沒環，肯定不相交；如果兩個都沒有環，判斷兩個列表的尾部是否相等；如果兩個都有環，判斷一個連結串列上的Z點是否在另一個連結串列上。

如何找到第一個相交的節點？求出兩個連結串列的長度L1,L2（如果有環，則將Y點當做尾節點來算），假設L1<L2，用兩個指標分別從兩個連結串列的頭部開始走，長度為L2的連結串列先走(L2-L1)步，然後兩個一起走，直到二者相遇。

Java程式碼

public static ListNode detectCycle(ListNode head) {
    ListNode slow = head;
    ListNode fast = head;

    while (true) {
        if (fast == null || fast.next == null) {
            return null;    //遇到null了，說明不存在環
        }
        slow = slow.next;
        fast = fast.next.next;
        if (fast == slow) {
            break;    //第一次相遇在Z點
        }
    }

    slow = head;    //slow從頭開始走，
    while (slow != fast) {    //二者相遇在Y點，則退出
        slow = slow.next;
        fast = fast.next;
    }
    return slow;
}