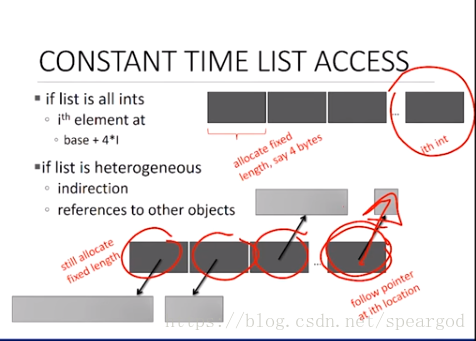
為什麼 retrieve（檢索）element of list 所花的時間是不變的？

因為假如list 都是ints 的話 ，每一個element  存在記憶體裡 需要4個位元組，那麼一個有著n個element的list在記憶體裡儲存的形式是這樣的， 給他一個連續的 4n個位元組的空間  儲存 元素， 所以當要檢索第i個元素的時候 我們直接去 base+4*i 個位元組去找就好了

（base是第0個元素存的地方） 所以花費的時間是不變的

那麼如果元素不全是 ints  是更復雜的情況的時候呢？ 

其實我們用的是linked list 的方法儲存列表的，對於n個元素的list 我們建立了一個n*一個固定長度的 的東東， 在這裡存的是n個指標，分別指向自己對應的元素， 所以當我們要檢索第i個元素 的時候，我們直接找第i個指標 然後通過指標 找到那個元素  所以時間還是固定的。

二分法：

龜龜，注意下面這個程式，他的複雜度不是O(logn)  

因為在遞迴的時候他還幹了一件事 copy  而list的copy的複雜度是 O(n)

所以真正的複雜的是O(nlogn) 當然具體的應該是更小，因為這個copy的size每次都變小 但也應該大於等於O(logn) （下面黑圖片，教授的話有解釋）

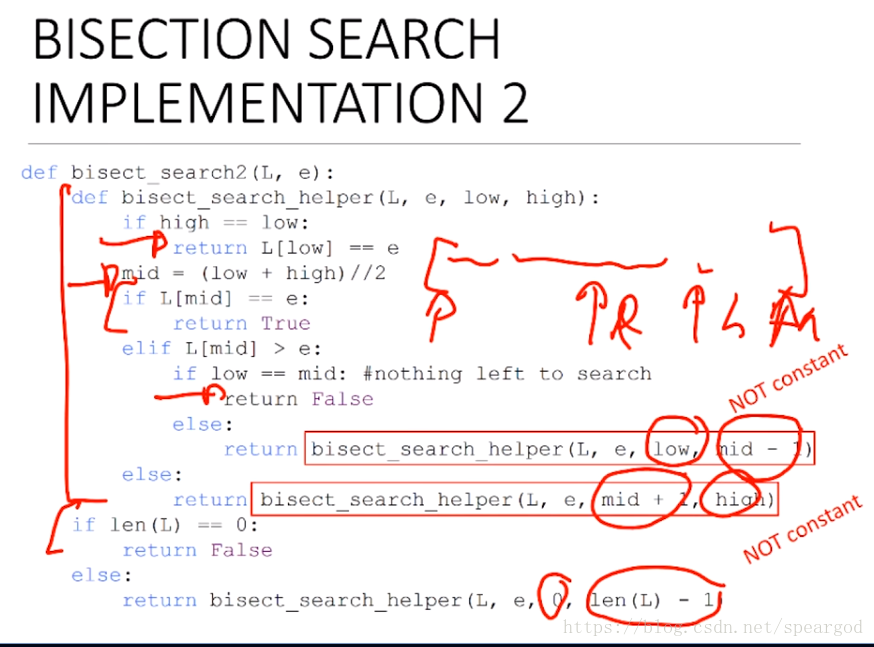
那麼怎麼避免這個copy呢， 請看下面這個程式：

這裡說的not constant  應該是說遞迴這個操作不是一個固定的時間 不是 O(1)  這個程式的複雜度其實是    O(logn)

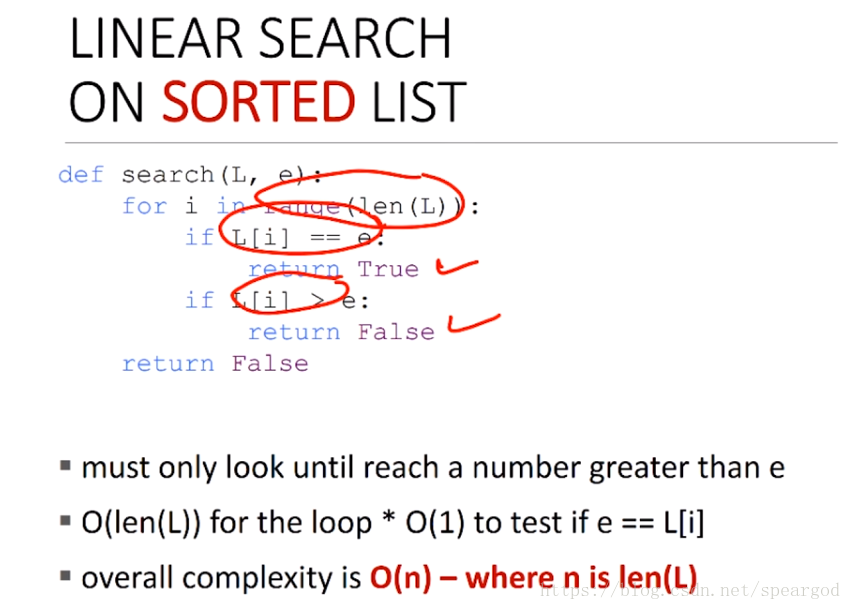
對於沒有sort 的list 來說  是直接linear search 好呢？還是先sort 再 二分查詢 好呢？

通常來說  假如你只做 一次 操作  那應該是 linear 好， 但是假如你要幹很多次操作呢？ 那sort花費的時間 就能分攤到每次操作上了   amortize（分攤）

幾種排序方法：

（1） monkey sort

就是拿到一個list 先看是不是 有序的，如果是 輸出，如果不是 瞎雞兒排 ，再看是不是有序的，一直重複直到找到有序的結果。

實現程式碼：

（2）bubble sort  氣泡排序

　氣泡排序的基本思想是，先比較第0個和第1個，如果小的在前 ，那麼不交換，反之交換，然後比較第1個和第2個 同理，一直這麼比較到最後第二個 和最後一個  那麼這一趟下來 最後一個的元素就是最大的，

然後下一趟，這次不包含最後一個元素了，最後一個比較是最後第3個和最後第2個  

一直這麼幹下去，直到某一趟沒有交換，或者最後只剩一個第一元素的時候  結束。

對相鄰的元素進行兩兩比較，順序相反則進行交換，這樣，每一趟會將最小或最大的元素“浮”到頂端，最終達到完全有序

　　程式碼實現

　　　　在氣泡排序的過程中，如果某一趟執行完畢，沒有做任何一次交換操作，比如陣列[5,4,1,2,3]，執行了兩次冒泡，也就是兩次外迴圈之後，分別將5和4調整到最終位置[1,2,3,4,5]。此時，再執行第三次迴圈後，一次交換都沒有做，這就說明剩下的序列已經是有序的，排序操作也就可以完成了，來看下程式碼　

這裡的程式碼不是很有效，因為這裡每次都比了 n-1次 但實際可以每進行一次比較，下次都可以少一次，

具體修改:

def bubble(L):
    swap = False
    i = 0
    while not swap:
        swap = True
        for j in range(1,len(L)-i):
            if L[j-1] > L[j]:
                swap = False
                L[j],L[j-1] = L[j-1],L[j]           
        i += 1

　　根據上面這種冒泡實現，若原陣列本身就是有序的（這是最好情況），僅需n-1次比較就可完成；若是倒序，比較次數為 n-1+n-2+^...+1=n(n-1)/2，交換次數和比較次數等值。所以，其時間複雜度依然為O(n²）。

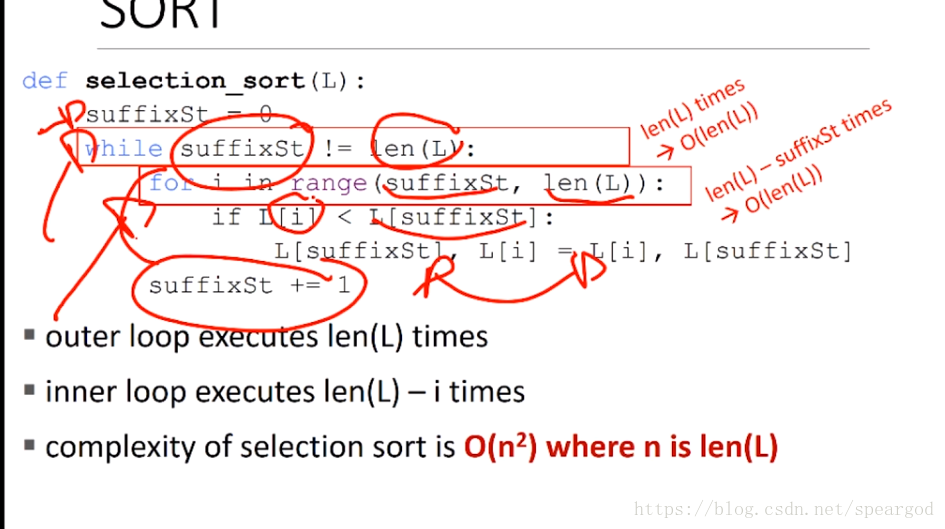
(3) 選擇排序

這個的思想就是先從  list 中選出最小的一個 把他和第0個元素交換， 然後再從除了第0個元素以外的元素 選出最小的 放在 第一個元素位置上，一直這麼幹下去

證明這個演算法是對的：（其實就是數學歸納法了）

程式碼實現：

複雜度 仍是O(n^2)  不過 教授說這個比冒泡好一點  雖然不懂為什麼）

（4） merge sort  歸併排序

先講歸併是咋回事：  

歸併 就是把兩個已經sort 好了的list  弄成一個 list  而且這個list是  order 好了的（從小到大或者從大到小）

那咋歸併呢 ？假設順序是從小到大  方法是  弄一個 空list  叫result，然後 比較 order好了兩個list（A,B）的 第一個元素 誰小誰  append 到 result   假如A 的第一個小，那接下來比較A的第二個元素和B的第一個元素……這麼一直比較下去，知道有個list比完了，那麼就把另一個list 剩下的元素 全部append 到result   就ok了  

下面就是歸併的程式碼：

然後我們可以看他的複雜度 ，應該就是兩個list的長度和    O(len（A）+len（B）)

但問題是現實不可能給兩個order 好了的list 給咱啊，一般就是一個無序的list  讓咱排序，那咋辦？

這就用到了 遞迴思想，啥叫遞迴？遞迴就是把一個大問題變成一些小問題加上一些簡單操作。

到這個歸併排序的問題的時候 我們就把對一個長度為n的無序的list A 排序的問題 變成  對A 前半部分排序和後半部分排序（一些小問題） 再歸併成一個序列（一些簡單操作）  的問題

那base 情況是啥呢？ 就是如果A的length 小於2的時候 也就是1或者0 這時候直接返回A 就好了，因為已經排好序了

下面是程式碼：

那這個遞迴的次數是多少呢？  因為每個stage 都把list的size 變成一半了  所以應該是O(logn)

那每個stage的複雜度是啥呢？ 

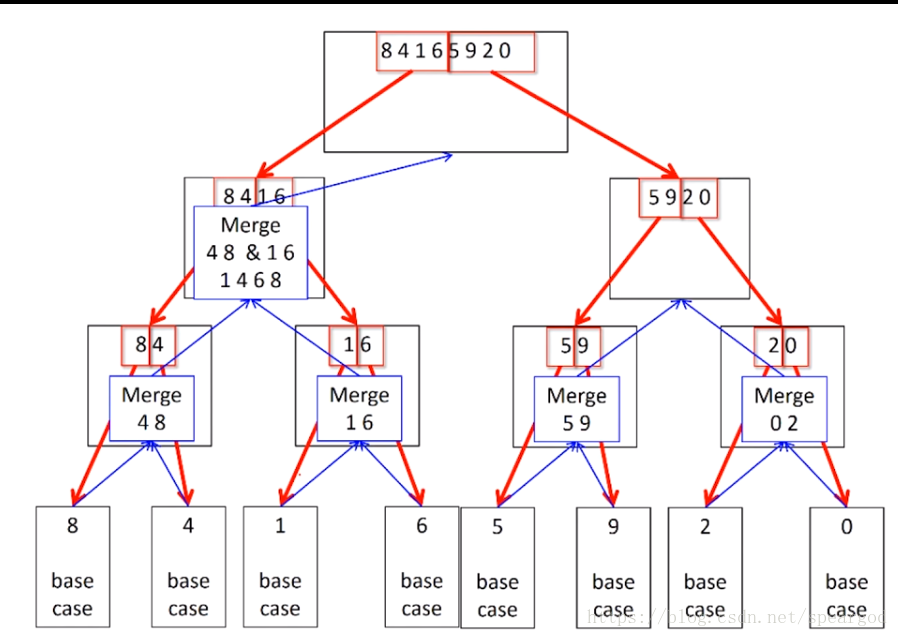
請看下圖： 

之前咱知道  歸併的複雜度是兩個list 的size和，雖然每一個stage  list的size都變一半了 ，但是每個stage 要歸併的變兩倍了啊 ，所以每個stage 的複雜度還是O(n)

所以總的複雜度是O(nlogn)

總結：

教授說 O(nlogn) 是所有sort方法 可以達到的最快的了  ，不知道是指這節課的sort 方法  還是所有的sort方法。