正態分佈

　　判斷一樣本所代表的背景總體與理論正態分佈是否沒有顯著差異的檢驗。

方法一概率密度曲線比較法

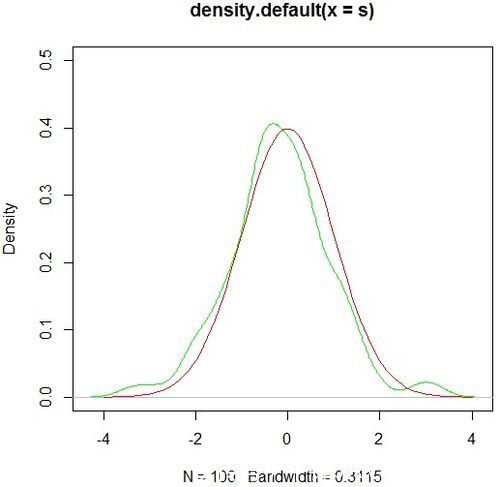
　　看樣本與正太分佈概率密度曲線的擬合程度，R程式碼如下：

　　#畫樣本概率密度圖s-rnorm(100)#產生樣本d-density(s)plot(d,col=green,ylim=c(0,0.5))#新增正太分佈概率密度圖s2-seq(from=-4,to=4,length.out=100)lines(s2,norm_expression(s2),col=red)

　　畫圖結果如下：

方法二 正太Q-Q圖法

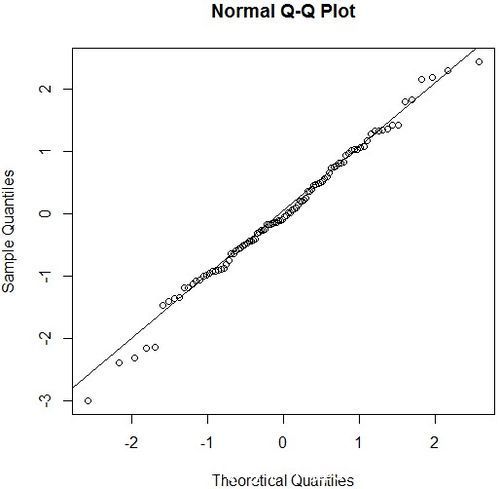
　　使用Q-Q圖來判斷資料是否服從正太分佈，R程式碼如下：

　　s-rnorm(100)#產生樣本qqnorm(s)qqline(s)

　　畫圖結果如下，可見資料分佈集中在對角線上，可以認為總體服從正太分佈：

方法三 經驗法則

　　約68.3%數值分佈在距離平均值有1個標準差之內的範圍，約95.4%數值分佈在距離平均值有2個標準差之內的範圍，以及約99.7%數值分佈在距離平均值有3個標準差之內的範圍。稱為“68-95-99.7法則”或“經驗法則”。

　　使用R的驗證程式碼如下：s-rnorm(10000)#產生樣本sum(abs(s-mean(s))sd(s))/length(s)sum(abs(s-mean(s))2*sd(s))/length(s)程式結果：s-rnorm(10000)#產生樣本sum(abs(s-mean(s))sd(s))/length(s)[1]0.6871sum(abs(s-mean(s))2*sd(s))/length(s)[1]0.9538

方法四 統計檢驗方法

　　使用樣本偏度和樣本峰度來估計總體偏度和峰度，在正太分佈的假定下，樣本偏度和峰度均服從均值為零、方差分別為6/T和24/T的正太分佈，可以分別檢驗偏度和峰度，也可以將兩個統計量結合起來生成一個服從自由度為2的卡方分佈的統計量，再進行檢驗【參見《金融時間序列分析》第三版P8~P9】。理論方面的東西略...

　　可以使用夏皮羅-威爾克(Shapiro-Wilk)檢驗，程式碼如下：

　　s-rnorm(1000)#產生樣本shapiro.test(s)

　　檢驗結果:

　　shapiro.test(s)Shapiro-Wilknormalitytestdata:sW=0.9987,p-value=0.6716

　　shapiro.test函式輸出一個p值，照慣例，p0.05說明總體不太可能是正太分佈，否則不能提供這麼個證據，也就是說這個檢驗比較保守，傾向於錯誤的過分證明正態性。

​