圖 | 深度優先生成樹和廣度優先生成樹
阿新 • • 發佈:2018-12-28
本章的第一節中,介紹了有關生成樹和生成森林的有關知識,本節來解決對於給定的
無向圖,如何構建它們相對應的生成樹或者生成森林。
其實在對無向圖進行遍歷的時候,遍歷過程中所經歷過的圖中的頂點和邊的組合,就是圖的生成樹或者生成森林。
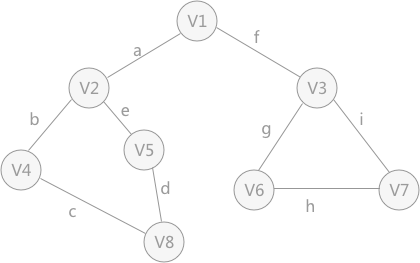
例如,圖 1 中的無向圖是由 V1~V7 的頂點和編號分別為 a~i 的邊組成。當使用深度優先搜尋演算法時,假設 V1 作為遍歷的起始點,涉及到的頂點和邊的遍歷順序為(不唯一):

此種遍歷順序構建的生成樹為:
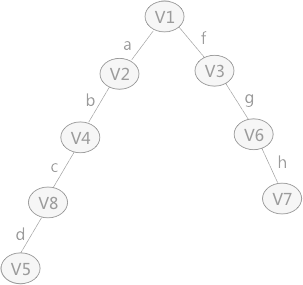
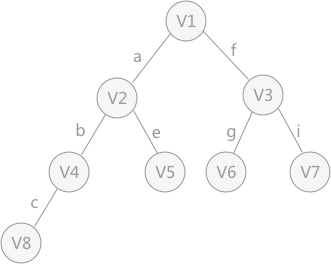
由深度優先搜尋得到的樹為`深度優先生成樹`。同理,廣度優先搜尋生成的樹為`廣度優先生成樹`,圖 1 無向圖以頂點 V1 為起始點進行廣度優先搜尋遍歷得到的樹,如圖 3 所示:
非連通圖的生成森林
非連通圖在進行遍歷時,實則是對非連通圖中每個連通分量分別進行遍歷,在遍歷過程經過的每個頂點和邊,就構成了每個連通分量的生成樹。
非連通圖中,多個連通分量構成的多個生成樹為非連通圖的生成森林。
深度優先生成森林
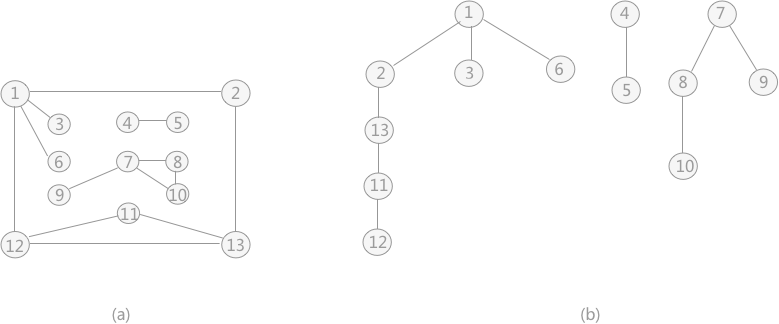
例如,對圖 4 中的非連通圖 (a) 採用深度優先搜尋演算法遍歷時,得到的深度優先生成森林(由 3 個深度優先生成樹構成)如 (b) 所示(不唯一)。
非連通圖在遍歷生成森林時,可以採用
孩子兄弟表示法將森林轉化為一整棵二叉樹進行儲存。
具體實現的程式碼:
#include <stdio.h>
#include <stdlib.h>
#define MAX_VERtEX_NUM 20 //頂點的最大個數
#define VRType int //表示頂點之間的關係的變數型別
#define VertexType int //圖中頂點的資料型別
typedef enum{false,true}bool; //定義bool型常量
bool visited[MAX_VERtEX_NUM] 執行程式,拿圖 4(a)中的非連通圖為例,構建的深度優先生成森林,使用孩子兄弟表示法表示為:
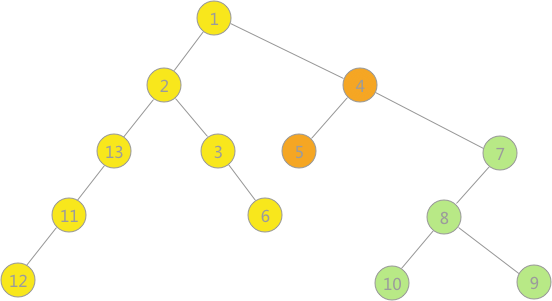
圖中,3 種顏色的樹各代表一棵深度優先生成樹,使用孩子兄弟表示法表示,也就是將三棵樹的樹根相連,第一棵樹的樹根作為整棵樹的樹根。
執行結果:
13,13
1
2
3
4
5
6
7
8
9
10
11
12
13
1,2
1,3
1,6
1,12
2,13
4,5
7,8
7,10
7,9
8,10
11,12
11,13
12,13
1 2 13 11 12 3 6 4 5 7 8 10 9
廣度優先生成森林
非連通圖採用廣度優先搜尋演算法進行遍歷時,經過的頂點以及邊的集合為該圖的廣度優先生成森林。
拿圖 4(a)中的非連通圖為例,通過廣度優先搜尋得到的廣度優先生成森林用孩子兄弟表示法為:
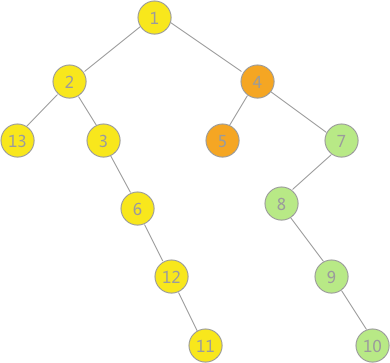
實現程式碼為:
#include <stdio.h>
#include <stdlib.h>
#define MAX_VERtEX_NUM 20 //頂點的最大個數
#define VRType int //表示頂點之間的關係的變數型別
#define InfoType char //儲存弧或者邊額外資訊的指標變數型別
#define VertexType int //圖中頂點的資料型別
typedef enum{false,true}bool; //定義bool型常量
bool visited[MAX_VERtEX_NUM]; //設定全域性陣列,記錄標記頂點是否被訪問過
typedef struct {
VRType adj; //對於無權圖,用 1 或 0 表示是否相鄰;對於帶權圖,直接為權值。
InfoType * info; //弧或邊額外含有的資訊指標
}ArcCell,AdjMatrix[MAX_VERtEX_NUM][MAX_VERtEX_NUM];
typedef struct {
VertexType vexs[MAX_VERtEX_NUM]; //儲存圖中頂點資料
AdjMatrix arcs; //二維陣列,記錄頂點之間的關係
int vexnum,arcnum; //記錄圖的頂點數和弧(邊)數
}MGraph;
typedef struct CSNode{
VertexType data;
struct CSNode * lchild;//孩子結點
struct CSNode * nextsibling;//兄弟結點
}*CSTree,CSNode;
typedef struct Queue{
CSTree data;//佇列中存放的為樹結點
struct Queue * next;
}Queue;
//根據頂點本身資料,判斷出頂點在二維陣列中的位置
int LocateVex(MGraph * G,VertexType v){
int i=0;
//遍歷一維陣列,找到變數v
for (; i<G->vexnum; i++) {
if (G->vexs[i]==v) {
break;
}
}
//如果找不到,輸出提示語句,返回-1
if (i>G->vexnum) {
printf("no such vertex.\n");
return -1;
}
return i;
}
//構造無向圖
void CreateDN(MGraph *G){
scanf("%d,%d",&(G->vexnum),&(G->arcnum));
for (int i=0; i<G->vexnum; i++) {
scanf("%d",&(G->vexs[i]));
}
for (int i=0; i<G->vexnum; i++) {
for (int j=0; j<G->vexnum; j++) {
G->arcs[i][j].adj=0;
G->arcs[i][j].info=NULL;
}
}
for (int i=0; i<G->arcnum; i++) {
int v1,v2;
scanf("%d,%d",&v1,&v2);
int n=LocateVex(G, v1);
int m=LocateVex(G, v2);
if (m==-1 ||n==-1) {
printf("no this vertex\n");
return;
}
G->arcs[n][m].adj=1;
G->arcs[m][n].adj=1;//無向圖的二階矩陣沿主對角線對稱
}
}
int FirstAdjVex(MGraph G,int v)
{
//查詢與陣列下標為v的頂點之間有邊的頂點,返回它在陣列中的下標
for(int i = 0; i<G.vexnum; i++){
if( G.arcs[v][i].adj ){
return i;
}
}
return -1;
}
int NextAdjVex(MGraph G,int v,int w)
{
//從前一個訪問位置w的下一個位置開始,查詢之間有邊的頂點
for(int i = w+1; i<G.vexnum; i++){
if(G.arcs[v][i].adj){
return i;
}
}
return -1;
}
//初始化佇列
void InitQueue(Queue ** Q){
(*Q)=(Queue*)malloc(sizeof(Queue));
(*Q)->next=NULL;
}
//結點v進佇列
void EnQueue(Queue **Q,CSTree T){
Queue * element=(Queue*)malloc(sizeof(Queue));
element->data=T;
element->next=NULL;
Queue * temp=(*Q);
while (temp->next!=NULL) {
temp=temp->next;
}
temp->next=element;
}
//隊頭元素出佇列
void DeQueue(Queue **Q,CSTree *u){
(*u)=(*Q)->next->data;
(*Q)->next=(*Q)->next->next;
}
//判斷佇列是否為空
bool QueueEmpty(Queue *Q){
if (Q->next==NULL) {
return true;
}
return false;
}
void BFSTree(MGraph G,int v,CSTree*T){
CSTree q=NULL;
Queue * Q;
InitQueue(&Q);
//根結點入隊
EnQueue(&Q, (*T));
//當佇列為空時,證明遍歷完成
while (!QueueEmpty(Q)) {
bool first=true;
//佇列首個結點出隊
DeQueue(&Q,&q);
//判斷結點中的資料在陣列中的具體位置
int v=LocateVex(&G,q->data);
//已經訪問過的更改其標誌位
visited[v]=true;
//遍歷以出隊結點為起始點的所有鄰接點
for (int w=FirstAdjVex(G,v); w>=0; w=NextAdjVex(G,v, w)) {
//標誌位為false,證明未遍歷過
if (!visited[w]) {
//新建一個結點 p,存放當前遍歷的頂點
CSTree p=(CSTree)malloc(sizeof(CSNode));
p->data=G.vexs[w];
p->lchild=NULL;
p->nextsibling=NULL;
//當前結點入隊
EnQueue(&Q, p);
//更改標誌位
vi
