上一節介紹瞭如何使用順序儲存結構儲存圖，而在實際應用中最常用的是本節所介紹的鏈式儲存結構：圖中每個頂點作為連結串列中的結點，結點的構成分為資料域和指標域，資料域儲存圖中各頂點中儲存的資料，而指標域負責表示頂點之間的關聯。

使用鏈式儲存結構表示圖的常用方法有 3 種：鄰接表、鄰接多重表和十字連結串列。

鄰接的意思是頂點之間有邊或者弧存在，通過當前頂點，可以直接找到下一個頂點。

鄰接表

使用鄰接表儲存圖時，對於圖中的每一個頂點和它相關的鄰接點，都儲存到一個連結串列中。每個連結串列都配有頭結點，頭結點的資料域不為NULL，而是用於儲存頂點本身的資料；後續連結串列中的各個結點儲存的是當前頂點的所有鄰接點

所以，採用鄰接表儲存圖時，有多少頂點就會構建多少個連結串列，為了便於管理這些連結串列，常用的方法是將所有連結串列的連結串列頭按照一定的順序儲存在一個數組中（也可以用連結串列串起來）。

總結起來，鄰接表的處理方法是這樣：

• 圖中頂點用一個一維陣列儲存，當然，頂點也可以用單鏈表來儲存，不過陣列可以較容易地讀取頂點資訊，更加方便。
• 圖中每個頂點 V_i 的所有鄰接點構成一個線性表，由於鄰接點的個數不確定，所以我們選擇用單鏈表來儲存。

在鄰接表中，每個連結串列的頭結點和其它結點的組成成分有略微的不同。各自的結構構成如下圖所示：

表頭結點結構：

• data 域儲存該頂點含有的資料；
• firstarc 為指標域，指向當前頂點的首個鄰接點。

其他節點結構：

• adjvex 儲存鄰接點在陣列中的位置下標；
• nextarc 指向下一個結點（鄰接點）的指標；
• info 記錄權值的資訊域。

info 域對於無向圖來說，本身不具備權值和其它相關資訊，就可以根據需要將之刪除。

例如，當儲存圖 2（A）所示的有向圖時，構建的鄰接表如圖 2（B）所示：

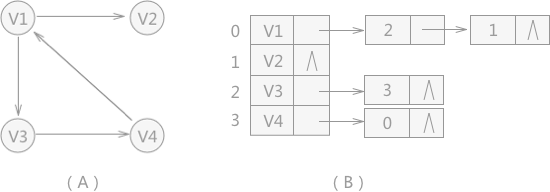
鄰接表儲存圖的儲存結構為：

#define
 
  MAX_VERTEX_NUM 20	//最大頂點個數
#define  VertexType int		//頂點資料的型別
#define  InfoType int		//圖中弧或者邊包含的資訊的型別

typedef struct ArcNode{
    int adjvex;				//鄰接點在陣列中的位置下標
    struct ArcNode * nextarc;//指向下一個鄰接點的指標
    InfoType * info;		//資訊域
}ArcNode;

typedef struct VNode{
    VertexType data;		//頂點的資料域
    ArcNode * firstarc;		//指向鄰接點的指標
}VNode,AdjList[MAX_VERTEX_NUM];//儲存各連結串列頭結點的陣列

typedef struct {
    AdjList vertices;		//圖中頂點及各鄰接點陣列
    int vexnum,arcnum;		//記錄圖中頂點數和邊或弧數
    int kind;				//記錄圖的種類
}ALGraph;

鄰接表計算頂點的度

使用鄰接表儲存無向圖時，各頂點的度為各自連結串列中包含的結點數；儲存有向圖時，各自連結串列中具備的結點數為該頂點的出度。求入度時，需要遍歷整個鄰接表中的結點，統計資料域和該頂點資料域相同的結點的個數，即為頂點的入度。

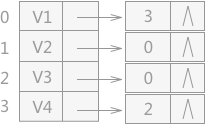
對於求有向圖中某結點的入度，還有一種方法就是再建立一個逆鄰接表，此表只用於儲存圖中每個指向該頂點的所有的頂點在陣列中的位置下標。例如，構建圖 2（A）的逆鄰接表，結果為：

對於具有 n 個頂點和 e 條邊的無向圖，鄰接表中需要儲存 n 個頭結點和 2e 個表結點。在圖中邊或者弧稀疏的時候，使用鄰接表要比前一節介紹的鄰接矩陣更加節省空間。

十字連結串列

十字連結串列儲存的物件是有向圖或者有向網。同鄰接表相同的是，圖（網）中每個頂點各自構成一個連結串列，為連結串列的首元結點。同時，對於有向圖（網）中的弧來說，有弧頭和弧尾。一個頂點所有的弧頭的數量即為該頂點的入度，弧尾的數量即為該頂點的出度。每個頂點構成的連結串列中，以該頂點作為弧頭的弧單獨構成一個連結串列，以該頂點作為弧尾的弧也單獨構成一個連結串列，兩個連結串列的表頭都為該頂點構成的頭結點。

這樣，由每個頂點構建的連結串列按照一定的順序儲存在陣列中，就構成了十字連結串列。

所以，十字連結串列中由兩種結點構成：頂點結點和弧結點。各自的結構構成如下圖所示：

弧結點結構：

• tailvex 和 headvex 分別儲存的是弧尾和弧頭對應的頂點在陣列中的位置下標；
• hlink 和 tlink 為指標域，分別指向弧頭相同的下一個弧和弧尾相同的下一個弧；
• info 為指標域，儲存的是該弧具有的相關資訊，例如權值等。

頂點結點結構（圖中頂點也是用一個一維陣列儲存，只是為了方便畫線沒有連在一起）：

• data 域儲存該頂點含有的資料；
• firstin 和 firstout 為兩個指標域，分別指向以該頂點為弧頭和弧尾的首個弧結點。

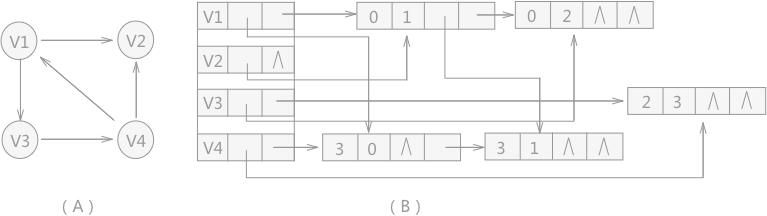
例如，使用十字連結串列儲存有向圖 5（A） ，構建的十字連結串列如圖 （B） 所示,構建程式碼實現為：

#define  MAX_VERTEX_NUM 20
#define  InfoType int		//圖中弧包含資訊的資料型別
#define  VertexType int

typedef struct ArcBox{
    int tailvex,headvex;	//弧尾、弧頭對應頂點在陣列中的位置下標
    struct ArcBox *hlik,*tlink;//分別指向弧頭相同和弧尾相同的下一個弧
    InfoType *info;			//儲存弧相關資訊的指標
}ArcBox;

typedef struct VexNode{
    VertexType data;		//頂點的資料域
    ArcBox *firstin,*firstout;//指向以該頂點為弧頭和弧尾的連結串列首個結點
}VexNode;

typedef struct {
    VexNode xlist[MAX_VERTEX_NUM];//儲存頂點的一維陣列
    int vexnum,arcnum;		//記錄圖的頂點數和弧數
}OLGraph;

int LocateVex(OLGraph * G,VertexType v){
    int i=0;
    //遍歷一維陣列，找到變數v
    for (; i<G->vexnum; i++) {
        if (G->xlist[i].data==v) {
            break;
        }
    }
    //如果找不到，輸出提示語句，返回 -1
    if (i>G->vexnum) {
        printf("no such vertex.\n");
        return -1;
    }
    return i;
}

//構建十字連結串列函式
void CreateDG(OLGraph *G){
    //輸入有向圖的頂點數和弧數
    scanf("%d,%d",&(G->vexnum),&(G->arcnum));
    //使用一維陣列儲存頂點資料，初始化指標域為NULL
    for (int i=0; i<G->vexnum; i++) {
        scanf("%d",&(G->xlist[i].data));
        G->xlist[i].firstin=NULL;
        G->xlist[i].firstout=NULL;
    }
    //構建十字連結串列
    for (int k=0;k<G->arcnum; k++) {
        int v1,v2;
        scanf("%d,%d",&v1,&v2);
        //確定v1、v2在陣列中的位置下標
        int i=LocateVex(G, v1);
        int j=LocateVex(G, v2);
        //建立弧的結點
        ArcBox * p=(ArcBox*)malloc(sizeof(ArcBox));
        p->tailvex=i;	//儲存弧尾對應的頂點在陣列中的位置下標
        p->headvex=j;	//儲存弧頭對應的頂點在陣列中的位置下標
        //採用頭插法插入新的p結點
        p->hlik=G->xlist[j].firstin;//指向弧頭相同的下一個弧；
        p->tlink=G->xlist[i].firstout;//指向弧尾相同的下一個弧；
        G->xlist[j].firstin=G->xlist[i].firstout=p;
    }
}

對於連結串列中的各個結點來說，由於表示的都是該頂點的出度或者入度，所以結點之間沒有先後次序之分，程式中構建連結串列對於每個新初始化的結點採用頭插法進行插入。

頭插法: 在連結串列的開頭插入一個新的節點，也就是，必須使得連結串列頭Head指向新節點，該新節點指向原來是表頭的第一個節點

Node newNode;			//生成新節點newNode
Node curr = head.next;
newNode.next = curr;	//新節點指向原來的第一節點
head.next = newNode;	//頭節點指向新節點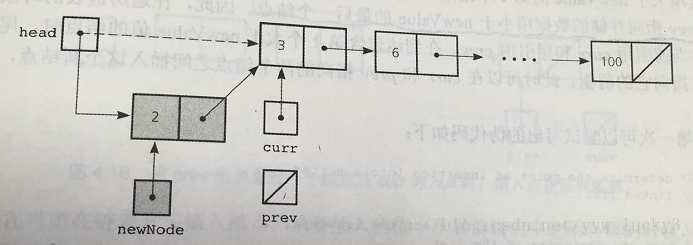

十字連結串列計算頂點的度

採用十字連結串列表示的有向圖，在計算某頂點的出度時，為 firstout 域連結串列中結點的個數；入度為 firstin 域連結串列中結點的個數。

鄰接多重表

使用鄰接表解決在無向圖中刪除某兩個結點之間的邊的操作時，由於表示邊的結點分別處在兩個頂點為頭結點的連結串列中，所以需要都找到並刪除，操作比較麻煩。處理類似這種操作，使用鄰接多重表會更合適。

例如，若要刪除(V0,V2)這條邊，就需要對鄰接表結構中邊表的兩個結點進行刪除操作。

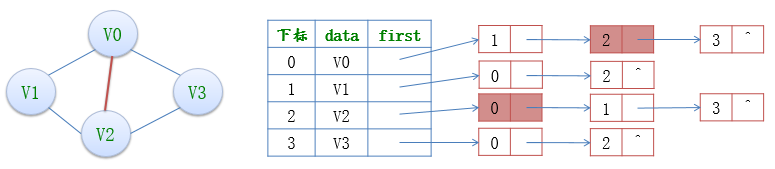
鄰接多重表可以看做是鄰接表和十字連結串列的結合體。和十字連結串列唯一不同的是頂點結點和表結點的結構組成不同；同鄰接表相比，不同的地方在於鄰接表表示無向圖中每個邊都用兩個結點，分別在兩個不同連結串列中；而鄰接多重表表示無向圖中的每個邊只用一個結點。

鄰接多重表的頂點結點和表結點的構成如圖 6 所示：

表結點構成：

• mark 為標誌域，作用是標記某結點是否已經被操作過，例如在遍歷各結點時， mark 域為 0 表示還未遍歷；mark 域為 1 表示該結點遍歷過；
• ivex 和 jvex 分別表示該結點表示的邊兩端的頂點在陣列中的位置下標；
• ilink 指向下一條與 ivex 相關的邊（或依附頂點 ivex 的下一條邊）；
• jlink 指向下一條與 jvex 相關的邊（或依附頂點 jvex 的下一條邊）；
• info 指向與該邊相關的資訊。

頂點結點構成：

• data 為該頂點的資料域；
• firstedge 為指向第一條跟該頂點有關係的邊。

例如，使用鄰接多重表表示圖 7中左邊的無向圖時，與之相對應的鄰接多重表如圖右側所示。

鄰接多重表的儲存結構用程式碼表示為：

#define MAX_VERTEX_NUM 20                   //圖中頂點的最大個數
#define InfoType int                        //邊含有的資訊域的資料型別
#define VertexType int                      //圖頂點的資料型別
typedef enum {unvisited,visited}VisitIf;    //邊標誌域

typedef struct EBox{
    VisitIf mark;                           //標誌域
    int ivex,jvex;                          //邊兩邊頂點在陣列中的位置下標
    struct EBox * ilink,*jlink;             //分別指向與ivex、jvex相關的下一個邊
    InfoType *info;                         //邊包含的其它的資訊域的指標
}EBox;

typedef struct VexBox{
    VertexType data;                        //頂點資料域
    EBox * firstedge;                       //頂點相關的第一條邊的指標域
}VexBox;

typedef struct {
    VexBox adjmulist[MAX_VERTEX_NUM];		//儲存圖中頂點的陣列
    int vexnum,degenum;						//記錄途中頂點個數和邊個數的變數
}AMLGraph;

總結

本節介紹了有關圖的三種鏈式儲存結構：鄰接表、十字連結串列和鄰接多重表。

鄰接表適用於所有的圖結構，無論是有向圖（網）還是無向圖（網），儲存結構較為簡單，但是在儲存一些問題時，例如計算某頂點的度，需要通過遍歷的方式自己求得。

十字連結串列適用於有向圖（網）的儲存，使用該方式儲存的有向圖，可以很容易計算出頂點的出度和入度，只需要知道對應連結串列中的結點個數即可。

鄰接多重表適用於無向圖（網）的儲存，該方式避免了使用鄰接表儲存無向圖時出現的儲存空間浪費的現象，同時相比鄰接表儲存無向圖，更方便了某些邊操作（遍歷、刪除等）的實現。