Welcome to part two of the predicting taxi fare using machine learning series! This is a unique challenge, wouldn’t you say? We take cab rides on a regular basis (sometimes even daily!), and yet when we’re hitting that ‘Book now’ button, we rely on manual on-the-fly calculations rather than hardcore ML ones. And that’s what I aim to demonstrate here.

In the previous post, we looked at cleaning the data and exploring it to identify relationships between variables, and also to understand various features that will have an impact on the Taxi Fare.

In this article, we will understand how to build machine learning models to predict taxi fare and look at the significant impact feature engineering plays in this process. The code for this article can be found

Roadmap

After the Data Cleaning and Exploratory Analysis phase, we have finally arrived at the Model Building phase. The quality of results at the end of this phase depends on the data quality and features used for modelling. In this article, we are going to understand the below steps in detail:

1. Data Preparation for model building
2. Creating a baseline prediction
3. Building Models without Feature Engineering
4. Building Models with Feature Engineering

Data Preparation

This step involves cleaning the data, dropping unwanted columns, converting the categorical variables to machine-understandable format, and finally splitting of training data into train and validation sets.

We will remove all negative fare amount, and passenger counts greater than 7, as we did in part 1.

The next step in data preparation is dividing the training data into train and validation data sets. This step is followed in almost all machine learning projects and is one of the most critical steps that allows us to evaluate models.

The validation dataset helps us understand how the model, fit using training data, works on any unseen data. This helps us gauge whether the model is overfitting or underfitting. Overfitting is the term used when training error is low, but the testing error is high. This is a common problem with complex models because they tend to memorize the underlying data and hence perform poorly on unseen data.

Simple models like Linear Regression do not memorize the underlying data, but instead have straightforward assumptions about the data. Therefore, these models have a very high error (high bias), but low variance. The validation data set will help us evaluate the models based on variance and bias. In this analysis, we will keep 25% of our data as validation data.

from sklearn.model_selection import train_test_splitX=train.drop([fare_amount],axis=1)y=train[fare_amount]X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.25,random_state=123)#test_size is the proportion of data that is to be kept aside for validation

Baseline Model

A baseline model is a solution to a problem without applying any machine learning techniques. Any model we build must improve upon this solution. Some ways of building a baseline model are taking the most common value in case of classification, and calculating the average in a regression problem. In this analysis, since we are predicting fare amount (which is a quantitative variable )— we will predict the average fare amount. This resulted in an RMSE of 9.71. So any model we build should have an RMSE lower than 9.71.

avg_fare=round(np.mean(y_train),2) #11.31baseline_pred=np.repeat(avg_fare,y_test.shape[0])baseline_rmse=np.sqrt(mean_squared_error(baseline_pred, y_test))print("Basline RMSE of Validation data :",baseline_rmse)

Model Building and Evaluation

1. Without Feature Engineering

In this step, we will use only DateTime features, without including any of the additional features like the trip distance, or distance from airports, or pickup distance from a borough. To understand and evaluate the models, we will consider the following ML algorithms:

• Linear Regression
• Random Forest
• Light GBM

Except for Linear Regression, the rest of the models are ensembles of decision trees, but they differ in the way the decision trees are created. Before we discuss further, let us understand the definitions of a couple of key terms we will be using.

1. Bagging: In this method, multiple models are created, and the output prediction is the average predictions of the different models. In Bagging, you take bootstrap samples (with replacement) of your data set and each sample trains a weak learner. Random Forest uses this method for predictions. In Random Forest, multiple decision trees are created, and the output is the average prediction by each of these trees. For this method to work, the baseline models must have a lower bias (error rate).
2. Boosting: In this method, multiple weak learners are ensembled to create strong learners. Boosting uses all data to train each learner. But instances that were misclassified by the previous learners are given more weight, so that subsequent learners can give more focus to them during training. XGBoost and Light GBM are based on this method. Both of them are variations of the Gradient Boosting Decision Trees (GBDTs). In GBDTs, the decision trees are trained iteratively — i.e., one tree at a time. XGBoost and Light GBM use the leaf-wise growth strategy when growing the decision tree. When training each decision tree and splitting the data, XGBoost follows level-wise strategy, while Light GBM follows leaf-wise strategy.

It’s finally time to build our models!

1. Linear Regression: It is used to find a linear relationship between the target and one or more predictors. The main idea is to identify a line that best fits the data. The best fit line is the one for which the prediction error is the least. This algorithm is not very flexible, and has a very high bias. Linear Regression is also highly susceptible to outliers as it tries to minimize the sum of squared errors.

lm = LinearRegression()lm.fit(X_train,y_train)y_pred=np.round(lm.predict(X_test),2)lm_rmse=np.sqrt(mean_squared_error(y_pred, y_test))lm_train_rmse=np.sqrt(mean_squared_error(lm.predict(X_train), y_train))lm_variance=abs(lm_train_rmse - lm_rmse)print("Test RMSE for Linear Regression is ",lm_rmse)print("Train RMSE for Linear Regression is ",lm_train_rmse)print("Variance for Linear Regression is ",lm_variance)

The test RMSE for Linear Regression model was 8.14, and the training RMSE was 8.20. This model is an improvement on the baseline prediction. Still, the error rate is very high in this model, though the variance is very low (0.069). Let’s try a more complex model next.

2. Random Forest

Random Forest is far more flexible than a Linear Regression model. This means lower bias, and it can fit the data better. Complex models can often memorize the underlying data and hence will not generalize well. Parameter tuning is used to avoid this problem.

rf = RandomForestRegressor(n_estimators = 100, random_state = 883,n_jobs=-1)rf.fit(X_train,y_train)rf_pred= rf.predict(X_test)rf_rmse=np.sqrt(mean_squared_error(rf_pred, y_test))print("RMSE for Random Forest is ",rf_rmse)

The Random Forest model gave an RMSE of 3.72 on validation data and train RMSE of 1.41. There is a huge variation in the training and validation RMSE, indicating overfitting. To reduce overfitting, we can tune this model.

3. LightGBM

LightGBM is a boosting tree based algorithm. The difference between Light GBM and other tree-based algorithms, is that Light GBM grows leaf-wise instead of level-wise. This algorithm chooses the node which will result in maximum delta loss to split. Light GBM is very fast, takes quite less RAM to run, and focuses on the accuracy of the result.

train_data=lgb.Dataset(X_train,label=y_train)param = {'num_leaves':31, 'num_trees':5000,'objective':'regression'}param['metric'] = 'l2_root'num_round=5000cv_results = lgb.cv(param, train_data, num_boost_round=num_round, nfold=10,verbose_eval=20, early_stopping_rounds=20,stratified=False)lgb_bst=lgb.train(param,train_data,len(cv_results['rmse-mean']))lgb_pred = lgb_bst.predict(X_test)lgb_rmse=np.sqrt(mean_squared_error(lgb_pred, y_test))print("RMSE for Light GBM is ",lgb_rmse)

This model gave an RMSE of 3.78 on validation data but the bias is higher than Random Forest. On the other hand, the variance of this model was 0.48 as compared to 2.31 in our Random Forest model.

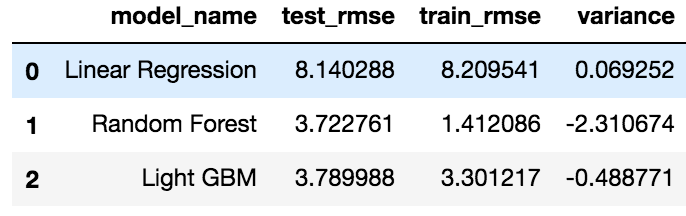
Since Light GBM has a comparable error rate to Random Forest, and has a lower variance and runs faster than the latter, we will use LightGBM as our model for further analysis

2. Feature Engineering and Model Tuning

Feature Engineering is the process of transforming raw data into features that are input to the final models. The aim is to improve the accuracy of the models. Having good features means we can use simple models for producing better results. Good features describe the structure inherent in the data.

As discussed in part 1, we will use features identified in the EDA phase, like the pickup and drop distance from airports, the pickup and drop distance from each borough (whether the pickup or drop was from or to the airport, and which borough the pickup or drop was from).

Applying the same Light GBM model discussed above on this feature engineered data resulted in an RMSE of 3.641 (drop from 3.78) and a variance of 0.48.

The next step is to tune this model. A good model has low bias and variance (to avoid overfitting). Few important features in LightGBM that can be optimized to reduce overfitting are:

1. max_depth: this indicates the maximum depth of the tree. Since LightGBM follows leaf-wise growth if not tuned, the depth can be much higher as compared to other tree-based algorithms.
2. subsample: This indicates what fraction of the data is to be used in each iteration, and it used to speed up the algorithm and control overfitting.
3. colsample_bytree: This is the fraction of features that are to be used in each iteration of the tree building process.
4. min_child_samples: This indicates the minimum number of samples that can be present in a leaf node. This helps to control overfitting.

I have used the hyperopt library in Python to tune the model. Hyperopt is a hyperparameter search package that implements various search algorithms to find the best set of hyperparameters within a search space. To use Hyperopt, we must specify an objective/loss function to minimize, the search space and trials database (optional, MongoTrials can be used to parallelise the search). For our problem, the objective is to minimise RMSE and identify the best set of parameters. We will tune the max_depth, subsample, and colsample_bytree parameters using hyperopt.

The objective function to be used for tuning is to minimize the RMSE in a LightGBM Regressor, given a set of parameters.

The search space defines the set of values a given parameter can take. After defining the objective function and the search space, we run 100 trials and evaluate the result of the trials on our validation data to identify the best parameters.

def objective(space):

clf = lgb.LGBMRegressor(          objective = 'regression',          n_jobs = -1, # Updated from 'nthread'          verbose=1,          boosting_type='gbdt',        num_leaves=60,        bagging_freq=20,       subsample_freq=100,    max_depth=int(space['max_depth']),    subsample=space['subsample'],        n_estimators=5000,    colsample_bytree=space['colsample'])          #metric='l2_root')

eval_set=[( X_train, y_train), ( X_test,y_test)]

clf.fit(X_train, np.array(y_train),            eval_set=eval_set,eval_metric='rmse',            early_stopping_rounds=20)

pred = clf.predict(X_test)    rmse = np.sqrt(mean_squared_error(y_test, pred))    print("SCORE:", rmse)

return{'loss':rmse, 'status': STATUS_OK }

space ={        'max_depth': hp.quniform("x_max_depth", 5, 30, 3),               'subsample': hp.uniform ('x_subsample', 0.8, 1),        'colsample':hp.uniform ('x_colsample', 0.3, 1)    }

trials = Trials()best = fmin(fn=objective,            space=space,            algo=tpe.suggest,            max_evals=100,            trials=trials)

print(best)

The best parameters that we got for LightGBM with feature engineering were:

{'max_depth': 24.0, 'subsample': 0.9988461076307639, 'colsample_bytree': 0.38429620148564814}

Using these parameters, the LightGBM model resulted in an RMSE of 3.633 and variance of 0.44. We can improve this model further by tuning other parameters like num_leaves and adding L1 and L2 regularisation parameters.

End Notes

Feature engineering significantly improved the predictive ability of our Machine Learning model. Another way to improve the model’s accuracy is to increase the amount of training data, and/or building ensemble models. If we have a lot of dimensions (features) in the data, dimensionality reduction techniques can also help improve the model’s accuracy.

I hope you found this article helpful. If you have any questions or feedback, please feel free to reach out in the comments section below.