I love generative art, and I frequently use a pseudo-random function to add a bit of noise to an image or behavior, but every time I implement a pseudo-random number function in JavaScript it takes me a second to remember how this works. So I thought I would write a quick post with a few of the most common pseudo-random number functions (henceforth referred to as simply “random” numbers) implemented in both vanilla ES6 and (just for fun) Python 3 as well. Of course there are infinitely many probability distributions and stochastic processes to explore, but I’ll keep this simple and save some useful concepts like

Markov chains and coherent noise for another time.

Decimals Between 0.0 and 1.0

The most basic way to generate a random number in JavaScript is the function Math.random() which returns a number n within the half-open interval such that 0 ≤ n < 1.

Remember that JavaScript does not discriminate between integers and decimals. All numbers in JavaScript are 64-bit floating point which may be written with or without decimals. To write a function that returns integers between 0 and n

we can use the JavaScript function confusingly named Math.floor(), which the MDN web docs tell us “returns the largest integer less than or equal to a given number.” Since Math.random() is half open, the function will also return an integer value n in the range 0 ≤ n < limit.

Python 3

The equivalent in Python is the function random.random()

from the random module (which similarly returns a half-open range). (Note that the common Python function random.uniform(a, b)differs in that it it returns a floating-point value n in the open interval a ≤ n ≤ b .)

Decimals Between 0.0 and 1.0 (Exclusive)

It is very unlikely that Math.random() will actually return the integer 0 — just one chance in 2⁵⁶ in fact — but for use cases where returning zero would have dire consequences, we can explicitly exclude that possibility. For example, we can make the function recursive only in case n == 0. In that case, the function will call itself and generate a new value.

function randomExcludingZero(min, max) {    n = Math.random() * (max - min) + min;    if (n > 0) {      return n;    }    else {      return randomExcludingZero(min, max);    }  }

Real Numbers Within a Range

Building on previous functions, we can write a more flexible random number function with a half-open range (a ≤ n <b) that can work with either integers or decimals. We can use a Boolean argument to switch between decimals and integers.

(Note that I’m initializing the function with an object here. Read Bill Sourour’s excellent post on the RORO pattern for a discussion of the advantages of doing this.)

function randomRange( { min, max, integers=true } ) {  if (integers) {    return (Math.floor(Math.random() * (max - min) + min));  }  else {    return (Math.random() * (max - min) + min);  }}

Python 3

Python has two built-in functions that return random numbers in a range, so the equivalent function in Python is significantly less verbose. (Remember that in Python the Boolean reserved words “True” and “False” use starting caps!)

import randomdef randomIntInc(min, max, integers=True):    if integers:        return random.randint(min, max)    else:        return random.uniform(min, max)

These functions works for all real numbers. We can pass negative numbers into either function so long as min ≤ max.

Choice of 1 or -1

Sometimes we want to randomly alternate between a number and its additive inverse. For example, if we have an object traveling along a vector, and we want to randomly reverse the direction of the object’s movement on that vector, we could multiply that vector by a random choice between 1 and -1.

In JavaScript we can implement this easily with a Ternary Operator. Basically we use Math.random() to generate a random decimal between 0.0 and 1.0. The function takes one argument which represents the chance that the function will return -1. If the random decimal falls bellow this limit, the function returns -1, otherwise the function returns 1. A limit of 0.5 will return a roughly uniform distribution of -1 and 1, while other values (< 1) will return a weighted distribution of -1s and 1s.

function additiveInverse(chanceOfNegative) { return (Math.random() < chanceOfNegative ? -1 : 1);}

Python 3

In this case the equivalent Python code is almost identical.

import randomdef additiveInverse(chanceOfNegative):    return 1 if random.random() < chanceOfNegative else -1

Random Array Without Repetitions

Sometimes we might need to generate an array filled with unique random values. To do this we need to give the function a minimum and maximum range (from which to select values) and specify the length of the array to generate. If our range is smaller than the length of the array, the function will enter an infinite loop because the function will exhaust all possible values before the array is full. A simple fix for this is to throwan exception just in case the absolute-value distance between the min and max fails to exceed arrayLength.

if (arrayLength > Math.abs(min - max)) {    throw "Array length fails to exceed range."}

Next we use a while-loop to fill an empty array. We generate a random number, check that the number is not already included in the array, and push that number onto the array only in case the number is unique.

Notice that we set the randomArray to empty by default from within the initialization of the function, not from within the body of the function.

function randomArrayWithoutReps( { min, max, arrayLength, randomArray = [], integers=true } )

This will be useful when we talk about streams of non-repeating numbers in the next section. Initializing the array this way lets us pass in a globally-scoped array if we want to, and since we initialize the function with an object, we also don’t have to pass in any value if we don’t want to when we call the function!

function randomArrayWithoutReps( { min, max, arrayLength, randomArray = [], integers=true } ) {

  if (arrayLength > Math.abs(min - max)) {    throw "Array length fails to exceed range."  }

  while (randomArray.length < arrayLength) {

    const randNum = integers       ? (Math.floor(Math.random() * (max - min) + min))       : (Math.random() * (max - min) + min);

    if (!randomArray.includes(randNum)) {       randomArray.push(randNum);    }  }  return randomArray;}

Python 3

Again, Python has a module function for random sampling, so all we have to do is call random.sample().

import randomrandom.sample(range(-10, 10), 12)

Random Stream Without (Recent) Repetitions

Sometimes we want to generate a stream of random numbers without repeating any values within the previous n number of function calls. Since the function will need some kind of “memory” of values it has generated recently, we’re probably going to end up using an array of some kind, and since we already have a function to generate arrays of random unique values, we can just build on that!

First we need to declare an empty array with global scope which will serve as our function’s “memory” of recently generated random values.

let randomBuffer = [];

function randomArrayWithoutReps({ min, max, arrayLength,   randomArray = [], integers=true }) {  [...]}

function randomStream({min, max, lengthWithoutRep, integers=true}) {    [...n] = randomArrayWithoutReps({     min: min,     max: max,     arrayLength: lengthWithoutRep,     randomArray: randomBuffer,     integers: integers });

randomBuffer = n;  return randomBuffer.shift();}

Our new function, randomStream, calls the randomArrayWithoutReps function we wrote earlier. Using destructuring we copy the output the random array function into the global randomBuffer variable. The .shift() method removes the first number in the global array and returns it as the output of our stream.

The trick here is that randomArrayWithoutReps is initialized each time with the newly updated global array. The function randomArrayWithoutReps looksat the incoming array, sees that it is one number short of its arrayLength, and computes a new unique value which it pushes onto the end of the array.

while (randomArray.length <= arrayLength) {  [...]  if (!randomArray.includes(randNum)) { randomArray.push(randNum); }  return randomArray;}

Essentially randomArrayWithoutReps functionsas a sliding window function which ensures that new random values do not repeat values generated within the previous n number of function calls. Pretty cool, right?

Python 3

In discussing random sampling for lists in Python above, I introduced Python’s random.sample() module function. If we want to create a random stream of numbers without repetitions within the last n number of values returned, a function with random.sample() might not actually be the best choice, because again that global randomBuffer variable serves as a kind of “memory” of values recently generated, so we’re going to have to update that list each time the function is called anyway. We can easily just do this with a while-loop as we did in JavaScript.

Using global variables in a function isn’t generally a best practice in Python, but here I think it clarifies the purpose of randomBuffer. (Don’t forget that we explicitly state that randomBuffer is a global variable at the start of each of our functions.) As in our JavaScript function, we use Python’s assert statement to throw an error if we are in danger of running out of potential random values before the buffer list is full. Most of the rest of the code is very similar to the JavaScript.

import timeimport randomfrom random import randint

randomBuffer = []

def randomListWithoutReps(minimum,                           maximum,                           listLength,                           integers=True):    global randomBuffer    assert listLength < abs(minimum - maximum), \    "List length fails to exceed range."    while len(randomBuffer) <= listLength:        if integers:            randNum = randint(minimum, maximum)        else:            randNum = random.uniform(minimum, maximum)        if randNum not in randomBuffer:            randomBuffer.append(randNum)    return randomBuffer

def randomStream(minimum,                  maximum,                  lengthWithoutRep):    global randomBuffer    randomBuffer = randomListWithoutReps(minimum,                                          maximum,                                          lengthWithoutRep)    return randomBuffer.pop(0)

To see the function in action, call it with something like this:

while True:    print(randomStream(0, 6, 5))    time.sleep(1)

Weighted Random Choice

Weighted sampling from an array is a method of non-uniform sampling in which each item in the array is assigned a weight representing that item’s odds of being selected. Weighted choice functions are very useful in games, digital art, and even web design because skewed probabilistic behaviors intuitively mimic many interactions we have with objects in the real world.

The goal here is to write a function that takes a list of relative probabilistic weightings and returns an index value between 0 and weights.length according to the relative weighting of the indices. This index value can then be used to return an item from another list of the same length.

Generally weighted choice functions are based on a total of all the weights in the array which is then partitioned according to the values of the weights and then iterated over. If a random number falls within one of the partitions, the index value of that partition is returned. However, an even more efficient algorithm avoids the temporary list of totals by subtracting each weight in the list from the random value variable. When the the variable is exhausted, we return that index.

function weightedRandom(weights) {  let rnd = Math.random() * weights.reduce((x, y) => x + y);  for (i = 0; i < weights.length; i++) {    rnd -= weights[i];    if (rnd < 0) {      return i    }  }}

Remember that the typical use case for this function is to return an index value that we use to select items from an array.

const favoriteFoods = ["sushi", "pizza", "falafel"]

document.getElementById("output").innerHTML =     favoriteFoods[weightedRandom([1, 1, 2])];

Since the list of weights is summed, the relative probability of an index being returned by the function is the ratio of that weight to the sum total of all the weights in the array. For example, the probability that the instance above will return “sushi,” “pizza,” or “falafel” is 25%, 25%, and 50% respectively.

Python 3

Python 3 does not have a weighted sampling method in its random module (although if you want to use Numpy you can call numpy.random.choice() which has an optional parameter fornon-uniform sampling). Eli Bendersky has a great blog post where he compares the efficiency of several weighted choice functions, so instead of trying to reinvent the wheel here, I’ll point you towards his blog post from 2010: “Weighted random generation in Python.” In fact, full disclosure, and my JavaScript function above is a port of his weighted_choice_sub Python function into ES6!

Random Walk

Random walks are basic processes encountered in a lot of digital art, and they have some pretty cool higher-dimensional implications too. A random walk is a stochastic process by which an entity or function is allowed to “move” (or returns a value) some distance away from its starting position or value. The function then takes on the value of it’s new position and may move again according to its “step size.” The step size may be binary (for example 1 or 0, i.e. movement or no movement) or the step size could be a random value within a range centered on the starting value. A random walk can also be constrained within a range, so when the “walker” reaches a boundary it is forced to turn around and step in the opposite direction.

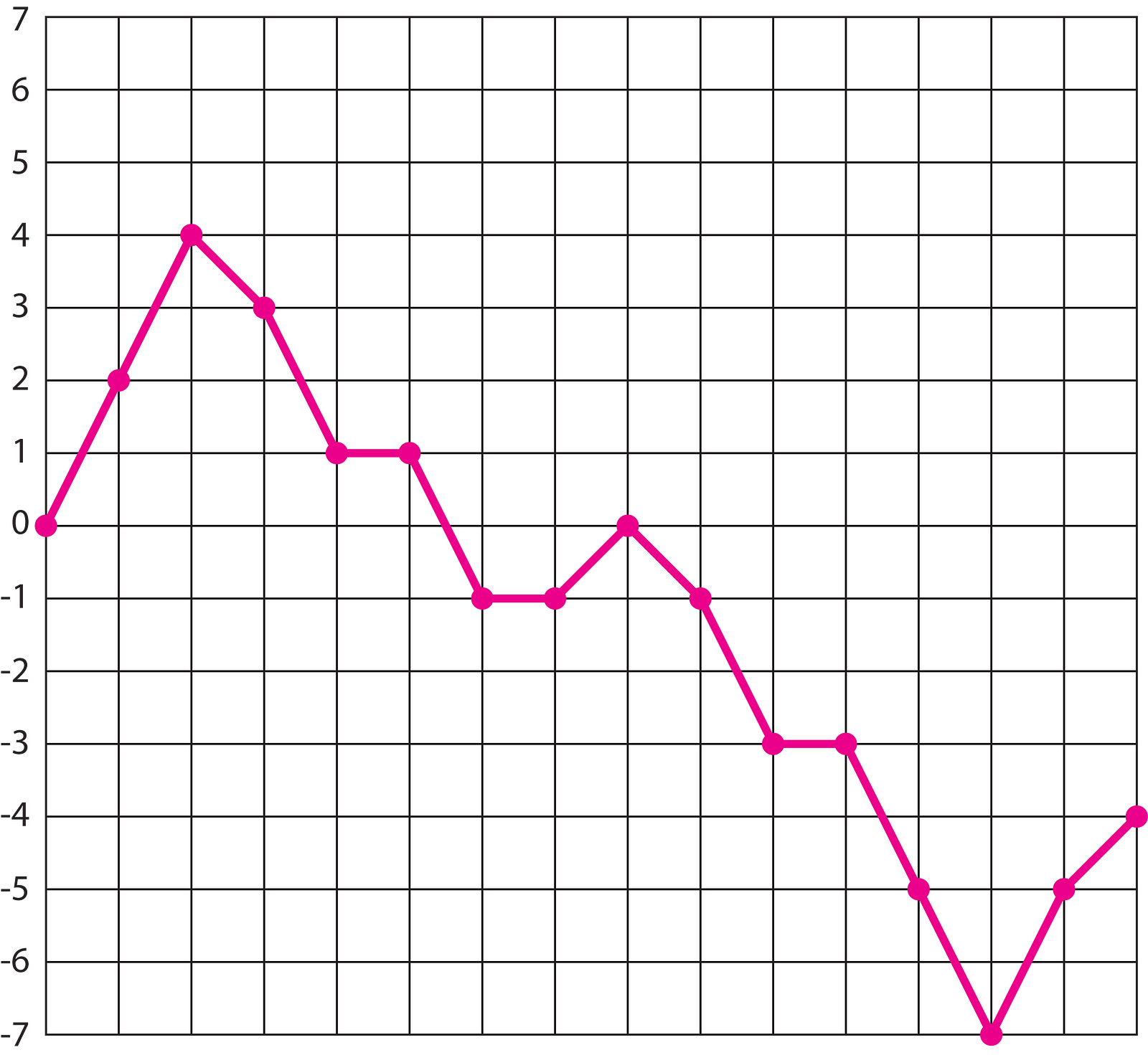
Since the state of the walker will be carried over from function call to function call we will need to define the walker as a mutable globally-scoped variable. Then we need to setup a function that will take our “walker,” a step size, and possibly a minimum and maximum boundary within which we will constrain the walk.

let walker = 0;

function randomWalk(walker, stepSize, min, max) {  ...}

Since our one-dimensional walk can either increase or decrease in value, we need a way to represent random changes in direction. This is where we can use our additive-inverse function from above. We’ll just get a uniform distribution of +/- values.

function randomWalk(walker, stepSize, min, max) {  const direction = (Math.random() < 0.5 ? -1 : 1);  ...}

If we want the walker’s rate of movement to be the same every time the function is called, we could just use “stepSize” as a constant:

function randomWalk(walker, stepSize, min, max) {  const direction = (Math.random() < 0.5 ? -1 : 1);  stepSize *= direction;  ...}

But it might be more interesting to have the “stepSize” define a range of possible values; to do this we use a random integer range:

function randomWalk(walker, stepSize, min, max) {  const direction = (Math.random() < 0.5 ? -1 : 1);  const step = Math.floor(Math.random() * stepSize) * direction;  ...}

Finally we need a conditional to check if the walker is about to overstep its upper or lower range. Notice that we are not checking whether the walker is currently at our outside of its range. We need to check if the walker will be outside of its range if it makes its next step.

if (((walker+step) <= max) && ((walker+step) >= min)) {  ...}

else {  ...}

If the current step is within the permissible range, we need to update the walker’s value and return the new value of the walker. If the current step will put the walker out of range, we reverse the direction of the step and return that value instead.

if (((walker+step) <= max) && ((walker+step) >= min)) {    walker += step;    return walker;  }else {    step *= -1;    walker += step;    return walker;  }

So all-together our function will look something like this. Of course when we call the function, we need to remember to set the value of “walker” to the returned value of the function or else the walker won’t walk very far!

let walker = 0;

function randomWalk( { walker, stepSize, min, max } ) {  const direction = (Math.random() < 0.5 ? -1 : 1);  const step = Math.floor(Math.random() * stepSize) * direction;  if (((walker+step) <= max) && ((walker+step) >= min)) {    walker += step;    return walker;  }  else {    step *= -1;    walker += step;    return walker;  }}

...

walker = randomWalk( { walker: walker, stepSize: 3, min: -7, max: 7 } )

Interesting effects can be achieved by having the step size or step direction of a random walk itself depend on a random walk. For example, if we want more of a stick-slip motion, we could use this technique to have a walker move in one direction for some number of consecutive steps before changing direction and moving for some other number of steps in another direction.

Python 3

The equivalent function in Python is pretty similar. Use the additive inverse function defined above to choose the step direction.

import randomwalker = 0;

def additiveInverse():    return 1 if random.random() < 0.5 else -1

def randomWalk(walker, stepSize, minimum, maximum):    direction = additiveInverse()    step = random.randint(0, stepSize) * direction    if (((walker+step) <= maximum) and ((walker+step) >= minimum)):        walker += step        return walker    else:        step *= -1        walker += step        return walker

...

walker = randomWalk(walker, 3, -7, 7)

Conclusion

Watch out for Nifflers…