For the past three years, humanity has known a new kind of astronomy from the traditional ones. No longer are we merely detecting light with a telescope, or neutrinos with enormous particle detectors, to give us an eye on the Universe. In addition to those, we’re also seeing, for the first time, the ripples inherent to space itself: gravitational waves. The LIGO detectors, now complemented by Virgo and soon to be joined by KAGRA and LIGO India, have extra-long arms that lengthen and contract as gravitational waves pass through them, giving rise to a detectable signal. But how does that work? Amrish Pandya wants to know, asking:

If the wavelength of light stretches and contracts with space-time, then how can LIGO detect gravitational waves. [Those waves] stretch and contract the two arms of the LIGO detector and so the the light waves within the the two arms [must] stretch and contract too. Wouldn’t the number of wavelengths of light in each arm remain the same hence cause no change in the interference pattern, rendering [gravitational waves] undetectable?

This is one of the most common paradoxes people think about when they consider gravitational waves. Let’s dive in to find the resolution!

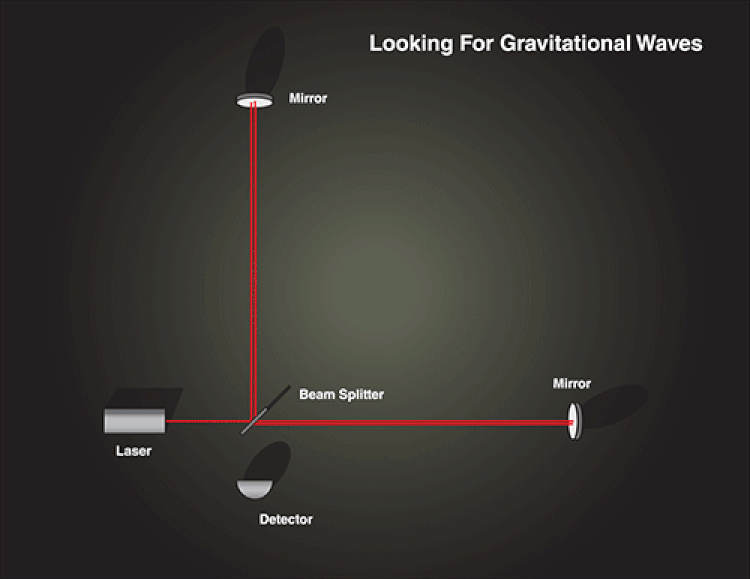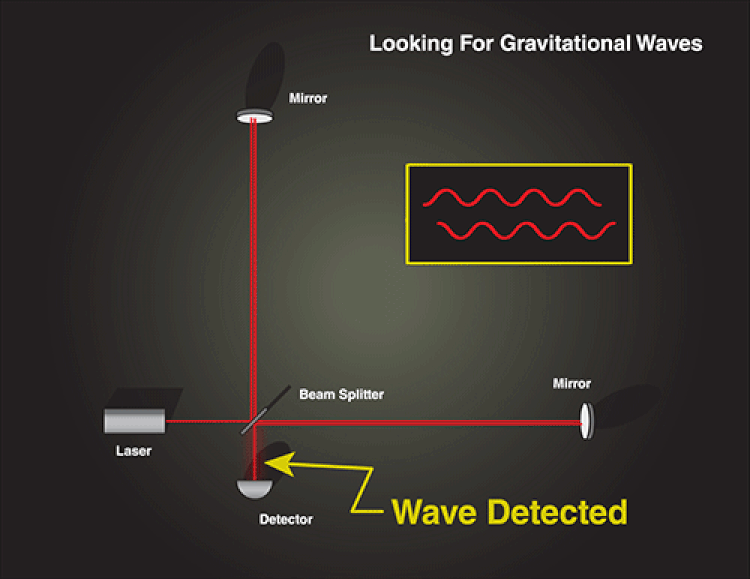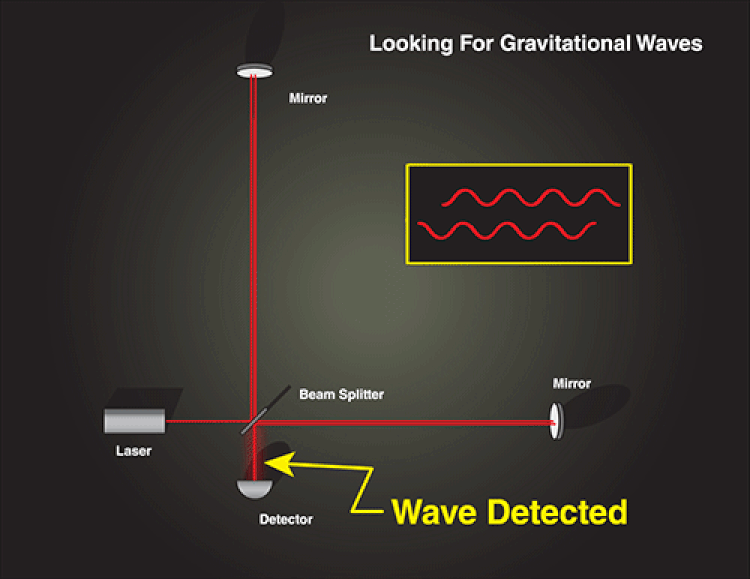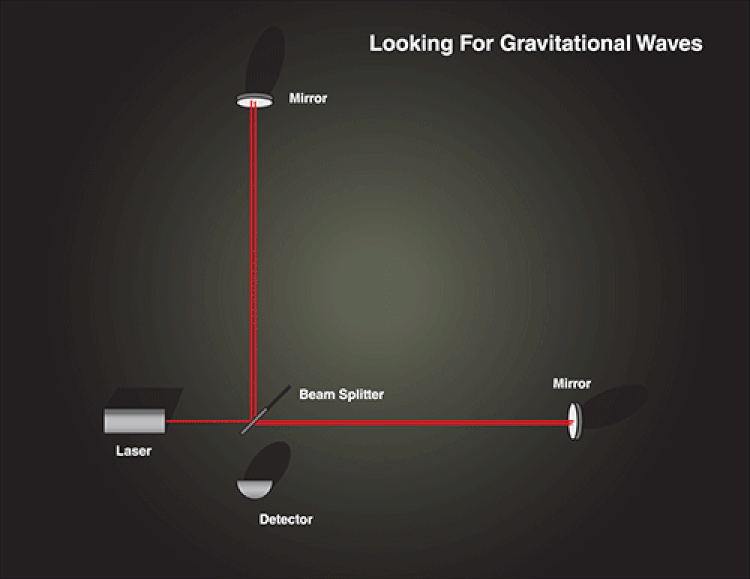
The way a gravitational wave detector, like LIGO, works is as follows:

• two long arms of exactly equal lengths and exact multiples of a particular wavelength of light are created,
• those arms are evacuated of all matter so that there is a perfect vacuum inside,
• coherent light (of the same wavelength) is split via a beam splitter into two perpendicular components,
• one is sent down one arm and one is sent down the other,
• the light is reflected many (thousands) of times between the two ends of each arm,
• and then the light is recombined, where it creates an interference pattern.

If the interference pattern remains absolutely constant in the absence of a gravitational wave signal, you know you’ve configured your detector properly. You know you’ve accounted for noise; you know you’ve set up your experiment correctly. This has been the struggle that LIGO has been working through for approximately 40 years: the attempt to calibrate their detector properly and bring down the sensitivity level to a point where it will be capable of detecting a true gravitational wave signal.

The magnitude of these signals are incredibly small, and that’s why it’s been such a challenge to reach the necessary precisions and accuracies.

Once you’re there, however, you’re ready to search for your actual signal. Gravitational waves are unique among all the different types of radiation produced in the Universe. Instead of detectable signatures that can interact with particles, gravitational waves are ripples through the fabric of space.

Instead of monopole (like charge-carrying) radiation or dipole (with oscillating fields, like electromagnetic) radiation, gravitational waves are a form of quadrupole radiation.

And instead of having in-phase electric and magnetic fields that run perpendicular to the direction of wave propagation, gravitational waves alternately stretch-and-compress the space they pass through in mutually perpendicular directions.

This is why we’ve constructed our detectors in the fashion we’ve built them. When a gravitational wave passes through a detector like LIGO, one of the arms will compress while the other expands, and then vice versa, in a mutually oscillatory pattern. The LIGO detectors are deliberately placed at angles to one another and at different locations on Earth’s surface, so that no matter what the orientation is that the wave passes through, at most one detector will be immune to the gravitational wave signal.

In other words, no matter how the gravitational wave is oriented, there will always be a detector that experiences one arm shortening while the other one lengthens, in a predictable, oscillatory fashion, so long as the wave passes through the detector.

So what does that mean for the light? Light always moves at the same, constant speed: c, or 299,792,458 m/s. That’s the speed of light in a vacuum, and LIGO has vacuum chambers inside both arms. The thing is, when a gravitational wave passes through each arm, lengthening or shortening the arm, it also lengthens or shortens the wavelength of the light within it by a corresponding amount.

This seems like a problem on the surface: if the light is lengthening or shortening as the arms lengthen or shorten, then the total interference pattern should remain unchanged as the wave passes through. At least, that’s what you would intuit.

But that’s not how it works. The wavelength of the light, which is highly dependent on how your space changes as a gravitational wave passes through, isn’t important for the interference pattern. What is important is the amount of time the light spends traveling through the arms!

When a gravitational wave passes through one of the arms, it changes the effective length of the arms, which therefore changes the amount of distance each laser beam needs to travel. One arm will lengthen, resulting in a longer light-travel time, while the other shortens, resulting in a shorter light-travel-time. As the relative arrival times change, we see an oscillatory pattern in how the reconstructed interference pattern shifts.

When the beams reunite, there’s a difference in the amount of time they’ve been traveling, and hence a detectable shift in the resulting interference pattern. The LIGO collaboration themselves has published an interesting analogy for this:

[…] imagine now that you and a friend want to compare how long it takes you to drive to the end of the interferometer arms and back. You agree to both travel at precisely 1 mile per hour. Just like LIGO’s laser light waves, you leave the corner station at exactly the same time and travel at precisely the same speed. You should meet up again at exactly the same time, shake hands, and move on. But let’s say you set out and half way along your journey, a gravitational wave passes. One of you now has a farther distance to travel, while the other has a shorter distance to travel. This means that one of you will return before the other. As you reach out to shake your friend’s hand, they’re not there! Your hand shake has been interfered with! Since you know how fast you were each traveling, you could measure how long it takes your friend to arrive, and then determine how much farther they had to travel in order to be late by that amount.

When you do this with light, as opposed to a friend, the measurement you use isn’t a delay in the arrival time (because the difference is something like 10–19 meters), but a shift in the observed interference pattern.

It’s true: light redshifts and blueshifts as a gravitational wave passes through the space that it occupies. As space compresses, the light’s wavelength compresses, making it bluer; as it rarifies, the wavelength stretches, making it redder. But those shifts are transient and relatively unimportant, at least, compared to the difference in path-length that the light must travel.

This is the key, important point in all of this: red light of long wavelengths and blue light of short wavelengths both take the same amount of time to traverse the same distance, even though it will take more crests-and-troughs of the blue light to make it. The speed of light in a vacuum is not affected by the light’s wavelength. The only factor that matters for the interference pattern is how far the light has to travel.

It’s the changing distance in path-lengths as a gravitational wave passes through a detector that determines the shifting in the interference patterns we see. As the wave passes through, one direction of the arms will lengthen, while the other simultaneously shortens, requiring a relative shift in the path-lengths and light-travel-times of the two arms.

Since the light moves through them both at the speed of light, the wavelength changes are unimportant; when they meet again, they’re at the same location in spacetime, and so their wavelengths will now be identical. What matters is that one beam of light spends longer in the detector, and so when they meet up again, they’re now out-of-phase. That’s where the LIGO signal comes from, and how we detect gravitational waves!