The Fitness Function

Camouflage is an important trait in the animal kingdom. It’s used by both predators and prey, and can be surprisingly sophisticated. So much so that to a lot of people it looks like these creatures had to have been designed:

The reason camouflage exists is because it’s an effective survival tool. It helps organisms survive long enough to pass on their genes, either by helping them to avoid being eaten, or by helping them to eat.

The algorithm I’ll show you today models how some really simple “organisms” can evolve to blend in with their “environment”.

So suppose there is some environment with some arbitrary background color and some organisms living on it. To start, these organisms will all have random colors, and will just be represented by circles.

Whether they are trying to avoid predators, or sneak up on prey, these organisms will need to blend in with their environment. Those that are closer to the color of their environment will tend to fare better and those that stick out more will fare worse.

Fitness is a term used to describe how well suited an organism is to its environment, and it’s what Darwin was referring to when he wrote “Survival of the Fittest”. In machine learning we have something called a

The fitness function is the invisible judge of what makes a “good” organism and what makes a “bad” one.

Here our fitness function is simple. Every organism has a different color, represented as an RGB value, and that color differs from the background color, which also has an RGB value. So the output of our fitness function is just the absolute value of the difference between an organism’s RGB values and the environment’s.

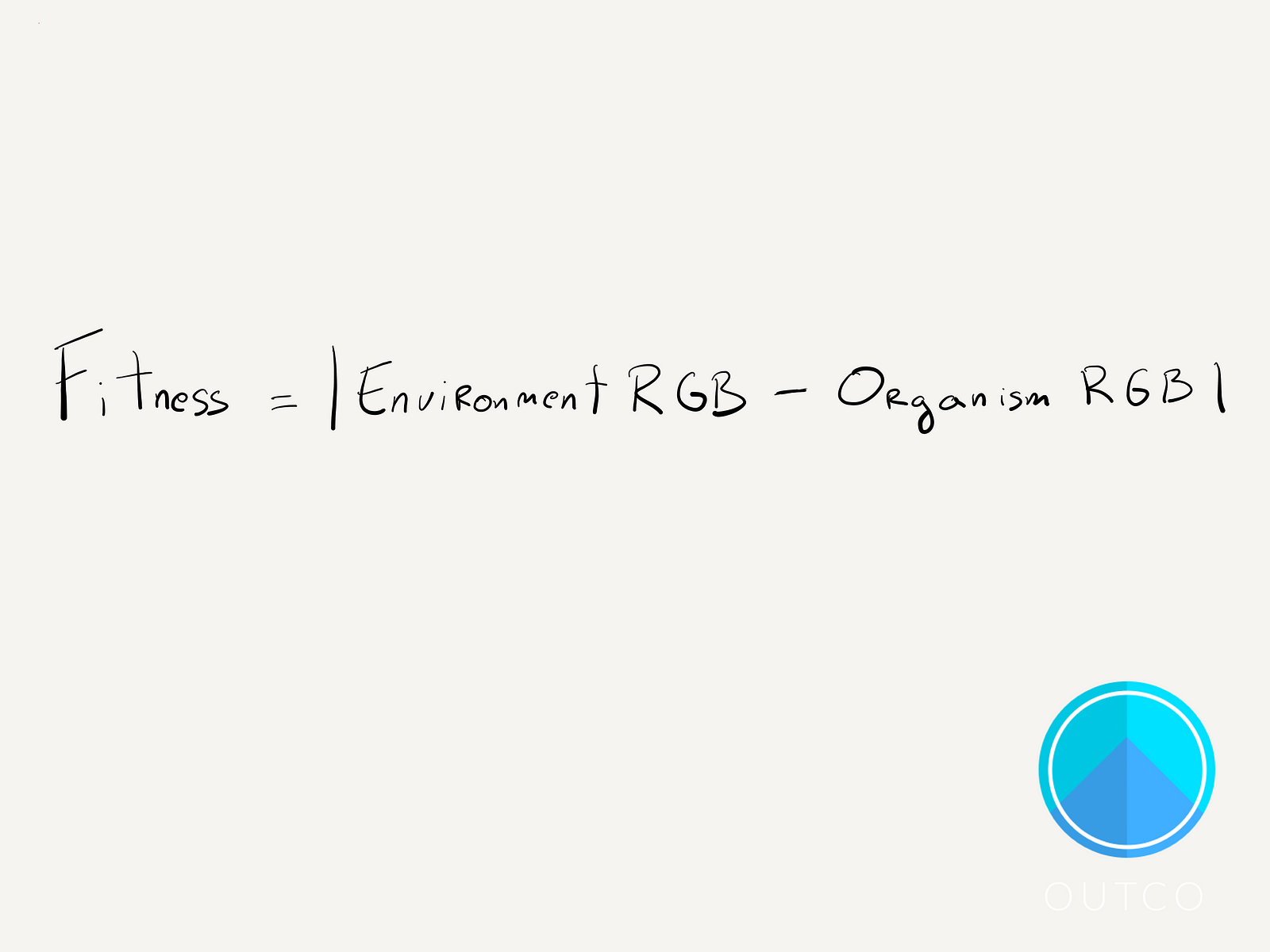
The more an organism’s color differs from the environment’s, the larger this value becomes. The maximum it could be is 765 (since the environment RGB values could be (0, 0, 0) and the organism’s could be (255, 255, 255)). And the minimum it could be is 0 if its color perfectly matches the environment’s.

Because a higher value actually means an organism sticks out more, I’m going to change the name from “fitness” to “weakness”, since an organism will want to minimize this value.

So let’s define our organisms:

class Organism {  constructor(r, g, b) {    this.r = r;    this.g = g;    this.b = b;  }}

And our environment:

class Environment {  constructor(r, g, b, startingOrganisms) {    this.r = r;    this.g = g;    this.b = b;    this.organisms = [];    this.weaknesses = [];    this.startingOrganisms = startingOrganisms;    this.addOrganisms(this.startingOrganisms);  }

  // Adds a list of organisms with random fitnesses  addOrganisms(num) {    while(num > 0) {

      let newOrganism = new Organism(randomValue(256),                                     randomValue(256),                                      randomValue(256));

      this.organisms.push(newOrganism);      this.weaknesses.push(this.calculateWeakness(newOrganism));      num -= 1;    }  }

  // Calculates weakness for a given organism  calculateWeakness(organism) {    return (Math.abs(this.r - organism.r) +             Math.abs(this.g - organism.g) +             Math.abs(this.b - organism.b));  }

The addOrganisms method generates an array of organisms with random RGB values, and the calculateWeakness method just adds up the differences between the environment’s RGB values and those of an organism.

Natural Selection

The second piece of the puzzle is applying pressure from this fitness function in the form of natural selection. The fitness function has to somehow affect an organism’s ability to survive and pass on its genes. Organisms with a lower weakness have a lower chance of being spotted by predators, and therefore have a lower probability of being killed because they stand out less, for example.

Natural Selection is the “invisible hand” of the system. It is the outside pressure that guides them towards being more adapted to their environment.

We’ll also be applying this fitness function over multiple generations of organisms. I’ll talk about how that looks later on, but just to give some sense of scale, for some of my simulations I ran over 20,000 generations (though each generation was only around 10ms long; more on that later).

There are many ways to implement a generation, but the way I decided on involves removing only a single individual from the population per generation, and replacing it with a new one.

But the decision of WHICH individual to remove is key .

Because to make this work, we want individuals that have a higher weakness to have a greater chance of being killed off. We want individuals that stand out from the background color more to be removed from the population with a greater likelihood.

The way I decided to do this was with some interval math.

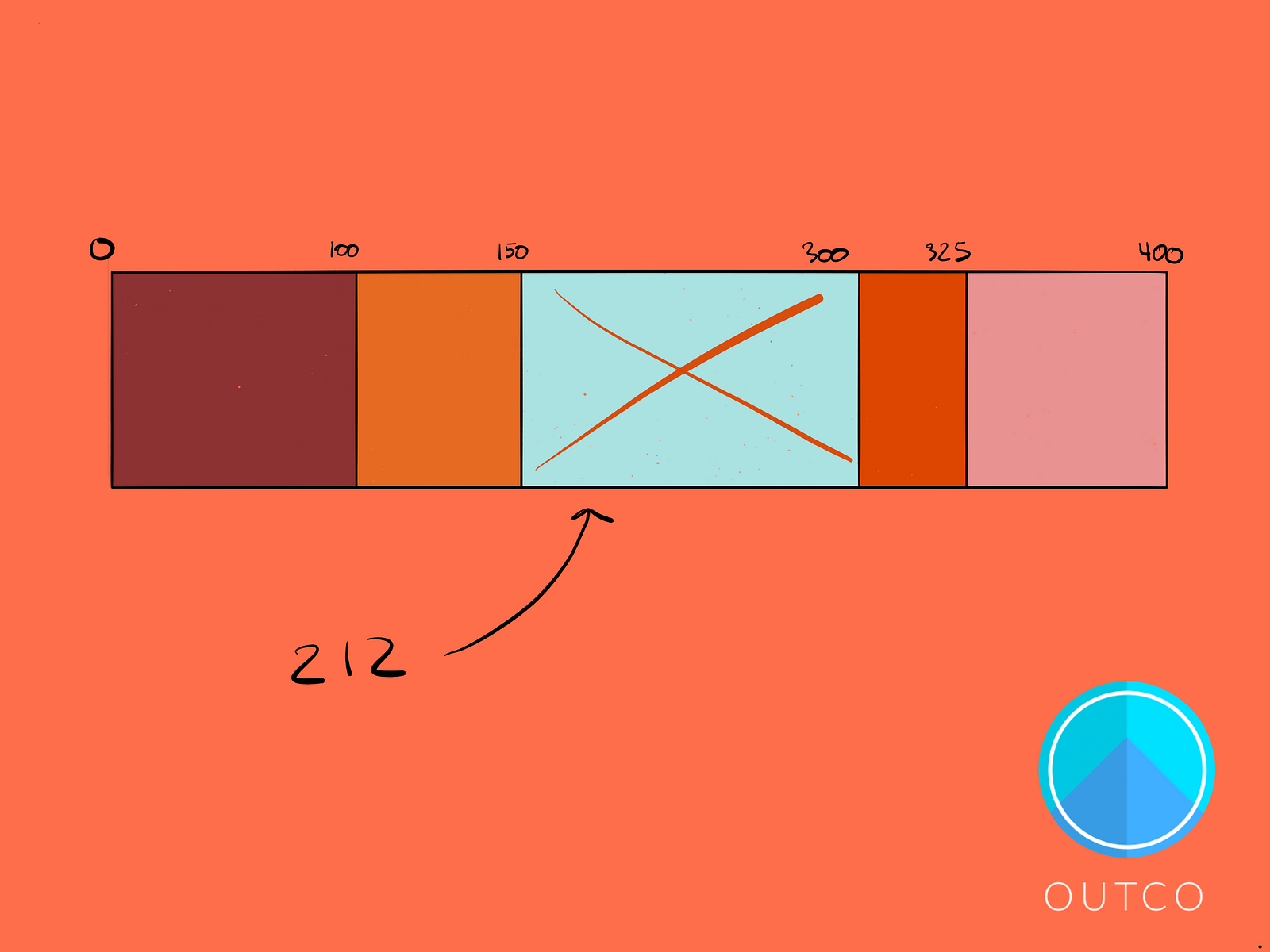
Imagine you have a rectangle, that is broken up into 5 segments of different lengths.

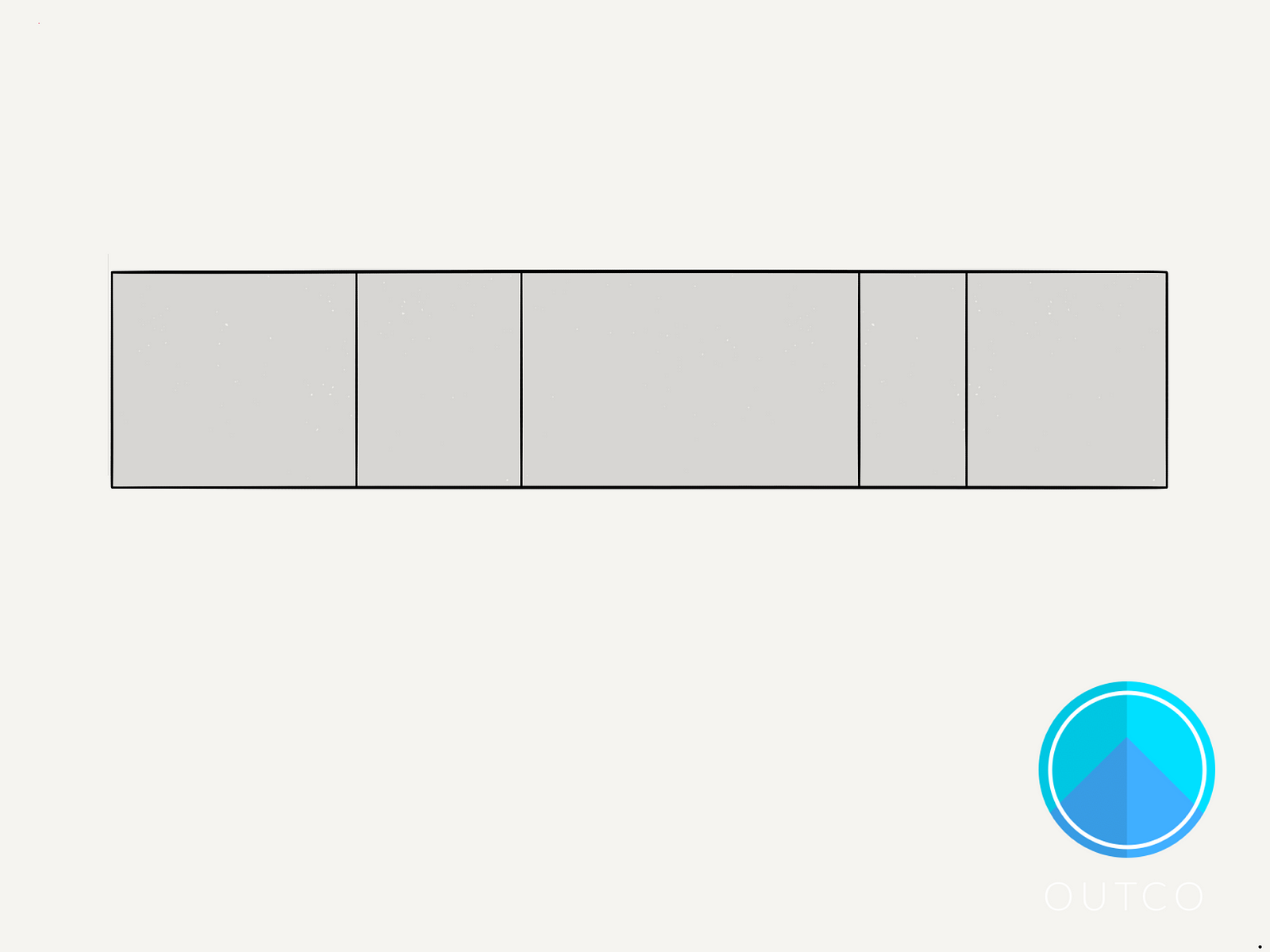
If you were to throw a dart at the rectangle, you’d expect the longest segment to have the highest chance of being hit because of the fact that it’s the longest.

Now let’s add some color.

The segment lengths are proportional to how far off an organisms color is from the background’s. The greater the difference, the longer the rectangle.

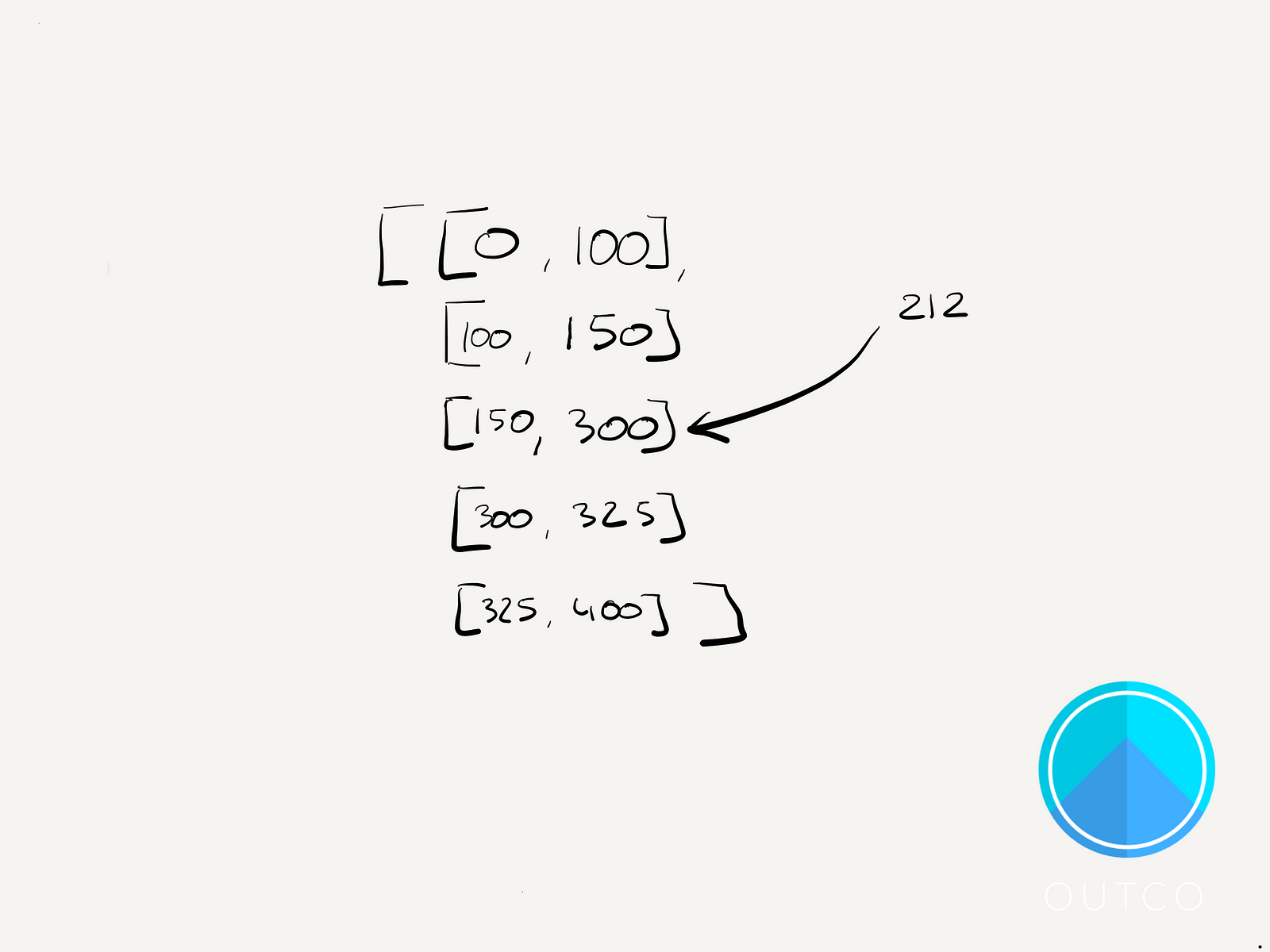
Now let’s add some numbers to define those ranges more clearly:

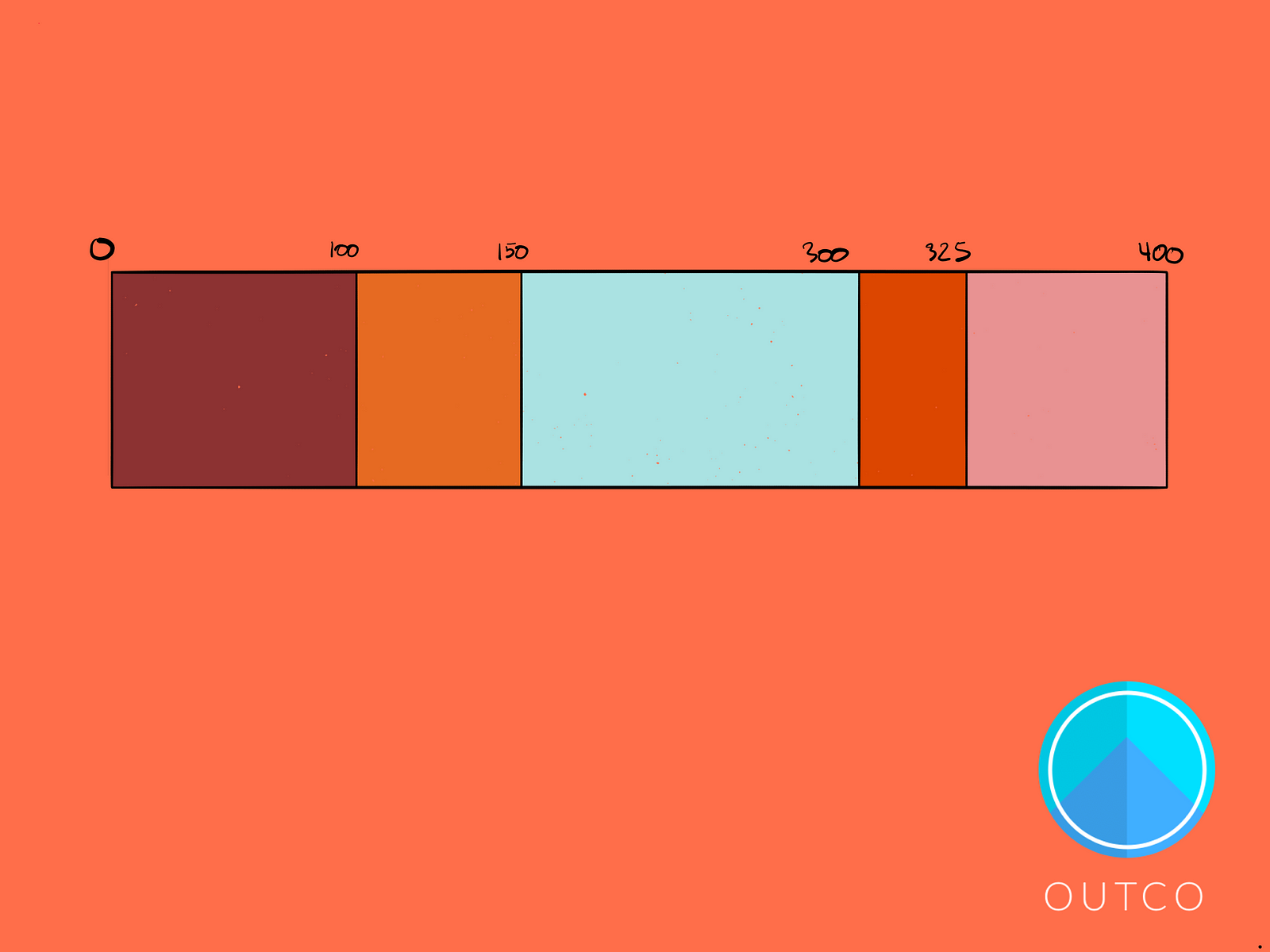
If we choose a random number between 0 and 400, that number has the greatest chance of falling between 150 and 300. But wherever it falls, let’s remove the corresponding organism.

The algorithm for this part is pretty straightforward.

1. We generate a random number in the total range (0–400)
2. Find the sub-range that contains that random number and remove that organism.

We can do this efficiently using a modified binary search, but since the number of ranges is small, we can just iterate from the first range until we find a range that contains the random number we’re looking for.

Let’s take a look at the code for natural selection:

replaceOrganism() {    let e = this;

// 1) Select a Random Organism to reproduce    let randomIndex = randomValue(this.organisms.length)    let parentOrganism = this.organisms[randomIndex];    let newOrganism = parentOrganism.reproduce();

// 2) Use intervals to weight individuals by weakness    let intervals = createIntervals(this.weaknesses);        //Sum of all weaknesses    let intervalRange = intervals[intervals.length - 1][1]; 

    let randomOrganismToReplace = randomValue(intervalRange);

// 3) Remove a random individual, weighted by weakness    intervals.forEach((interval, index) => {      if(isWithinInterval(interval, randomOrganismToReplace)) {        e.organisms[index] = newOrganism;        e.weaknesses[index] = e.calculateWeakness(newOrganism);      }    });

}

// Detect if number falls within a rangefunction isWithinInterval(interval, num) {  return interval[0] <= num && num < interval[1];}

// Creates Intervals from array of intsfunction createIntervals(arr) {  let runningTotal = 0;  let result = arr.map(int => {    let newTotal = runningTotal + int;    let result = [runningTotal, newTotal]    runningTotal = newTotal;    return result;  });  return result;}

We need to replace the organism we’re removing if we want to keep the population constant. Because reproduction with our creatures is asexual, we only have to select a single parent. We also have to decide WHEN we do the reproduction round; before or after we remove an individual. If we do it before, there’s a chance the individual we remove will pass on its genes.

In my code I opted for simplicity. I choose a random parent to have an offspring that would end up replacing whichever organism we remove later on. I also made it so all organisms have an equal probability of passing on their genes, even the ones with higher weaknesses.

But it needn’t have been this way. If I had done the replacement after the removal, it would have lowered the odds of “bad” genes being passed on and the population likely would have evolved more quickly. Or, we could have had some other way of measuring fitness (the inverse of weakness perhaps) as a way of increasing the probability of certain organisms passing on their genes.

Because at the end of the day, all we’re doing is weighting the probabilities of some organisms being selected for removal over others. We could easily do something similar for reproduction.

But the power of this system is that even by just weighting which organisms have a higher chance of being removed, the population will evolve over time to become more fit (ie closer to the background color).

Mutation

Though there is one final piece that’s missing and that’s mutation.

Without random mutations, ie slight variations between parent and child generations, we would not necessarily get greater fitness over time.

Instead, what would happen is that eventually the fitness level would stabilize at basically some arbitrary point. Just by random chance, one of the original organisms would take over, even if by luck alone. Because all that needs to happen is for it to have a single offspring and its chances are then doubled for passing on its genes to the next generation. Repeat that process a few more times and you get the possibility of an individual with lower fitness taking over the entire population.

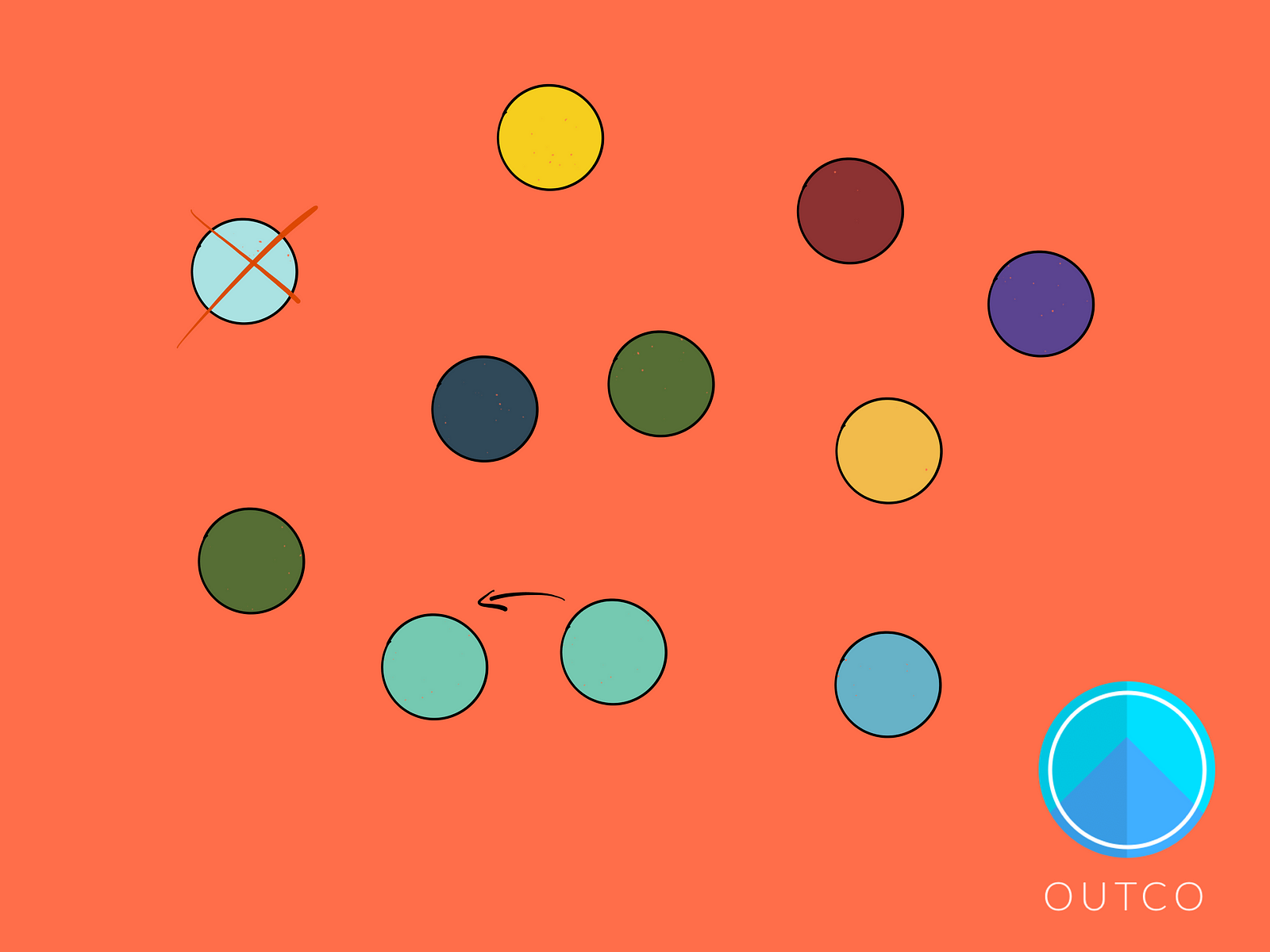
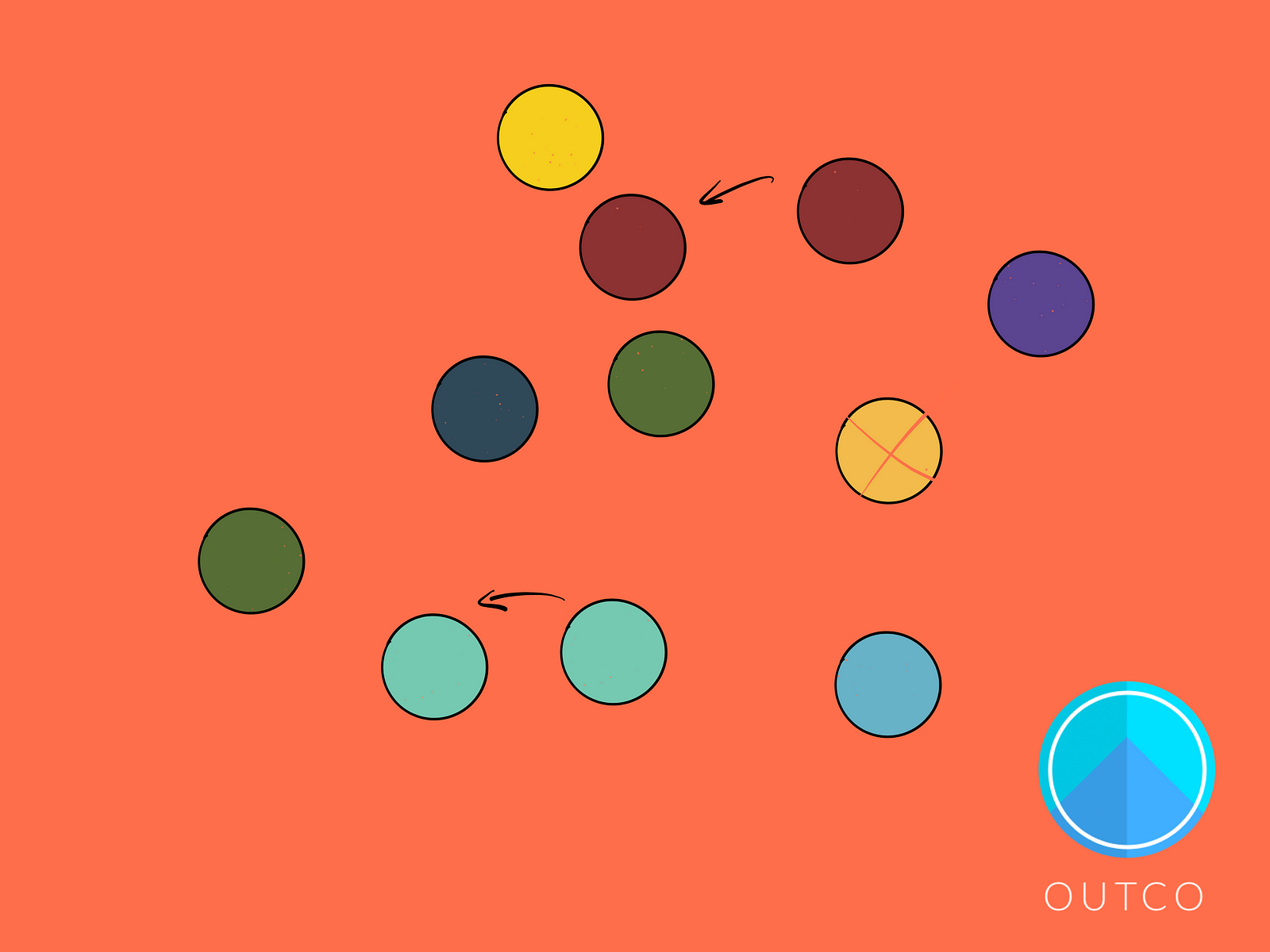
But even if the fittest individual from the start survived and took over, the population would stagnate, and would not continue to evolve over time.

This isn’t what we see in nature. In nature we see gradual change over time, and in fact we’ve even used it to our own benefit, artificially selecting tiny variations in traits we like, and weeding out the ones we don’t:

To model this behavior, we need to make it so that when an organism “reproduces”, the new organism it creates isn’t an EXACT copy. We want its RGB values to differ by some random, small amount from its parent’s. Sometimes a parent might create an exact copy, but usually it will mean offspring are either slightly more or less fit than their parent.

If you allow your mutations to be very large, the offspring can differ considerably from the parent generation, which isn’t necessarily something that you want. A large mutation rate makes it harder to reach stability in your population, and even if an organism reached some optimal fitness level, odds are its offspring would erase those beneficial traits in the next generation. So trying to “force” evolution with a high mutation rate doesn’t really work and usually leads to chaos.

Mutation is a subtle force, but a powerful one over long enough timespans. Because even if an organism with lower fitness manages to take over early on by chance, over time it will drift towards optimality. It’s like the erosive force of water that can carve out the grand canyon.

Slow and steady, the blind watchmaker does his work.

And in our example it doesn’t matter what the starting point is, the population will trend towards blending in with the environment. It doesn’t matter if initially the differences between organism and environment were small, or large. They will always converge to being same color.

In fact, if you changed the environment’s background color, the population of organisms would start to drift towards that new color instead. And you wouldn’t have to change a single line of code!

Here’s what all this looks like as methods on the Organism class:

reproduce() {    // Prevents negative numbers from appearing    let newR = Math.max(this.r + this.mutateTrait(), 0);    let newG = Math.max(this.g + this.mutateTrait(), 0);    let newB = Math.max(this.b + this.mutateTrait(), 0);    return new Organism(newR, newG, newB);  }

mutateTrait() {    let multiplier = Math.random() - 0.5;    if(multiplier < 0) {      return randomValue(this.mutationSize) * -1;    } else {      return randomValue(this.mutationSize);    }  }

Observations

Putting it all together, there are some key observations we can make.

In the code I’ve attached below, there are a few parameters to play around with.

The first is the generation time, which is just the number of milliseconds between cycles, where a single cycle involves removing an organism and generating a new mutant. You’ll want this to relatively small since it takes quite a few generations to see significant changes (again, some simulations I ran took 20,000 generations to reach optimality).

The second parameter is the population size. This is how many organisms are in the environment at any given time, and in this model that number is held constant. Generally speaking the larger the population, the more time it takes to reach some kind of optimum because it takes longer for “good genes” to take over the entire population.

The last parameter is the mutation rate. This one is key because it dictates the fate of the population. Make it too large, and the population never seems to stabilize and can’t trend toward anything. Make it too small and the population won’t evolve enough and the fitness level will get stuck. In my model there are also some quirks because of the way the math works out with flooring, so anything below 2 has this problem of getting stuck. But choose the right mutation rate and the whole population should eventually all match the background color.

One particularly interesting observation/hypothesis is that if the mutation rate is somewhere in the middle, the population will enter a dynamic equilibrium, where it seems to hover around a certain average weakness value. And it can be computed from this formula:

(number_of_traits * mutation_rate_per_trait)/2

In this case the number of traits is always 3 (rgb), and each one has the same mutation rate, so the average weakness is 1.5 times the mutation rate, with greater mutation rates having a higher deviations from that average.

Try it out for yourself, and let me know what you think!