深度優先搜尋(DFS)的奇偶剪枝
阿新 • • 發佈:2018-12-29
今天進行到DFS&&BFS&&活動網路問題。BFS和DFS可以解決很多有趣的問題,而BFS和DFS本身就有很多優化、變形。對於對於優化最常見的莫過於剪枝了,而對於搜尋剪枝,最常見的也就是奇偶剪枝。
先看沒有剪枝和剪枝之後的效果:

為什麼剪枝
因為DFS和BFS可以是認為樹形搜尋的。因此,他們的搜尋軌跡可以生成出深度優先生成樹和廣度優先生成樹,詳情見: 圖的連通性。
如果我們在生成樹的過程中(就是查詢過程中),發現並確定一個分支不可能找到解,那麼我們就把這個分支剪掉,以節省時間。這就是剪枝。
奇偶剪枝
首先我們要知道一個前提:
奇數 + 偶數 = 奇數
偶數 + 偶數 = 偶數
那麼,也就可以推出:
偶數 = 奇數 - 奇數
偶數 = 偶數 - 偶數
假設有這麼一個地圖:
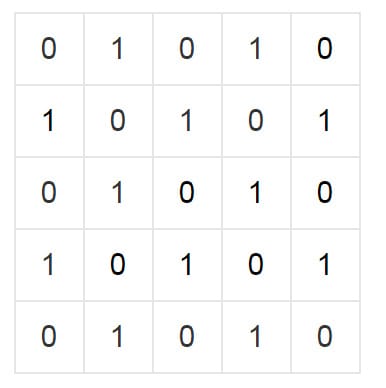
我們可以發現一個規律,從其中任意一個0到任意一個0需要偶數步,而其中任意一個1到任意一個0需要奇數步。
如果我們每一步的消耗時間是相同的,那麼,需要用時和最短的步數必須需要同奇偶才能到達,否者不會到達。
為了方便描述,我們假設我們在(sx,sy)的位置,需要消耗t時到達(ex,ey)。
那麼不管我們怎麼繞圈,如果 t-[abs(ex-sx)+abs(ey-sy)] 結果為非偶數(奇數),則無法在t步恰好到達。
因此,這樣我們就可以在搜尋過程中,實時判斷現在剩下的時間和現在位置到目的地最短距離是否同奇偶,如果不是,那麼就沒有必要搜尋下去了。
骨頭問題
再回到ZOJ2110,這個題用到了奇偶剪枝,並且還有一種搜尋前優化,就是如果所有狗狗能走的位置(所有的地圖位置的個數減去障礙物的個數)小於規定時間,直接列印NO(就是狗狗根本跑不開,就不用搜索了)。
程式碼:
#include <iostream> #include <cstring> #include <cmath> using namespace std; char mp[10][10]; int bj[10][10]; int chx[] = {0,1,0,-1}; int chy[] = {1,0,-1,0}; int n,m,t; int ex,ey; int tf; void dfs(int x,int y,int tim) { if(x < 0 || y < 0 || x >= n || y >= m) return ; if(tim == t && x == ex && y == ey) { cout << "YES" << endl; tf = 1; return ; } int tmp = (t - tim) - fabs(x - ex) - fabs(y - ey); if(tmp < 0 || tmp % 2) return ; for(int i = 0; i < 4;i++) { if(mp[x + chx[i]][y + chy[i]] != 'X') { mp[x + chx[i]][y + chy[i]] = 'X'; dfs(x + chx[i],y + chy[i],tim + 1); if(tf) return ; mp[x + chx[i]][y + chy[i]] = '.'; } } } int main() { while(cin >> n >> m >> t,n) { tf = 0; memset(bj,-1,sizeof(bj)); for(int i = 0;i < n;i++) cin >> mp[i]; int x,y; for(int i = 0;i < n;i++) { int j; for(j = 0;j < m;j++) if(mp[i][j] == 'S') { x = i; y = j; break; } if(j < m) break; } for(int i = 0;i < n;i++) { int j; for(j = 0;j < m;j++) if(mp[i][j] == 'D') { ex = i; ey = j; break; } if(j < m) break; } mp[x][y] = 'X'; dfs(x,y,0); if(!tf) cout << "NO" << endl; } return 0; }

歡迎到微信裡去當吃瓜群眾
