使用Matlab完成層次聚類演算法(最小生成樹演算法)
阿新 • • 發佈:2018-12-29
最近要寫作業,涉及到一些聚類演算法。
關於聚類演算法的一些理論和定義,請參照部落格http://blog.sina.com.cn/s/blog_62f3c4ef01014uhe.html 和大傳送術http://blog.csdn.net/a1b2c3d4123456/article/details/45966429 這兩篇文章。
Matlab具體實現如下:
filename = 'C:\Users\zyfls\Desktop\ML\第七章聚類\chap_7_資料集.xlsx'; A = xlsread(filename); for i=1:500 data(i,1)=A(i,1); data(i,2)=A(i,2); end Y=pdist(data,'euclidean');%計算歐式距離 Y=squareform(Y);%轉換成方陣 Z=linkage(Y,'average');%引數為平均距離 figure(1); dendrogram(Z,0);%視覺化聚類樹 T=cluster(Z,3);%剪枝為三類 figure(2); for i=1:500 data(i,3)=T(i); if T(i)==1 plot(data(i,1),data(i,2),'r.'); else if T(i)==2 plot(data(i,1),data(i,2),'g.'); else T(i)==3 plot(data(i,1),data(i,2),'b.'); end end hold on; end
xlsx檔案是500個點的點座標。 原始碼中引數註釋如下 % 'single' --- nearest distance (default) % 'complete' --- furthest distance % 'average' --- unweighted average distance (UPGMA) (also known as % group average) % 'weighted' --- weighted average distance (WPGMA) % 'centroid' --- unweighted center of mass distance (UPGMC) % 'median' --- weighted center of mass distance (WPGMC) % 'ward' --- inner squared distance (min variance algorithm)
‘single’:最短距離法(預設);
‘complete’:最長距離法;
‘average’:未加權平均距離法;
‘weighted’: 加權平均法;
‘centroid’:質心距離法;
‘median’:加權質心距離法;
‘ward’:內平方距離法(最小方差演算法)
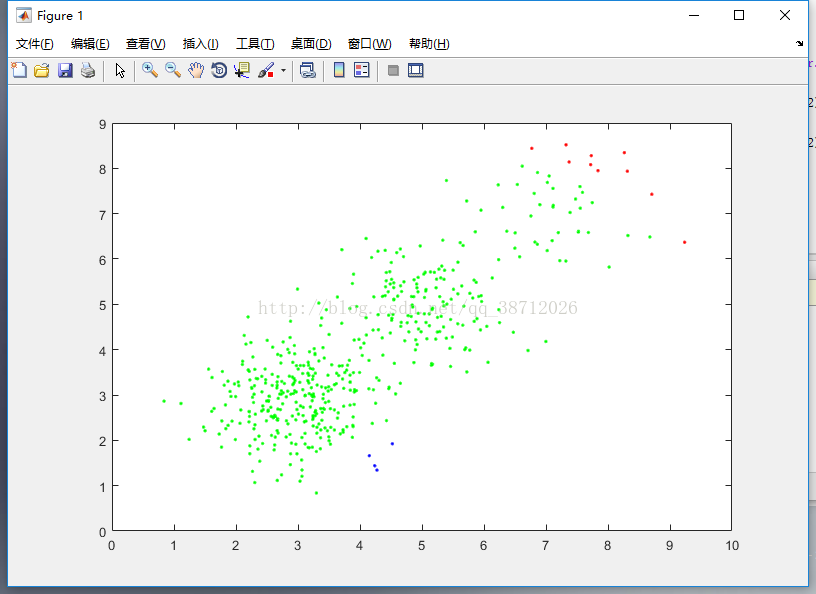
此程式碼使用average引數完成聚類,聚類效果如下:聚類樹效果如下:
另附single(最短距離)聚類引數效果如下:
weighted(加權距離)聚類引數效果如下:
其中方陣Y是得到任意兩點之間的歐式距離:
接下來Z=linkage(Y,'average');生成聚類樹,簡單說就是先找距離最近的兩點,將其歸為一類,接下來將這兩個點看作一個點繼續與其它點比較,從中再找最近的兩點,最後歸為一類。
總結,通過得到的聚類樹可以知道,最終會生成一個根節點,也就是聚類成為了一類,但是大多數情況下,我們會將其劃分為多類。對於這個例子來說,是分為三類。
所以要對聚類樹進行剪枝(我也不知道這是不是叫剪枝,覺得這個操作非常符合剪枝這個動作)。
程式碼中T=cluster(Z,3)完成了將Z的聚類結果分為了三類。具體理論上怎麼實現的,不太清楚,先挖個坑...