本人最近初學Hinton大神的論文《Dynamic Routing Between Capsules 》，對深度神經網路的內容進行了簡要總結，將觀看“從傳統神經網路的角度解讀Capsule”視訊的內容做了筆記。感謝網路資源，讓我學習到很多知識。以後會有更新。

作者： 嫩芽33
出處： http://www.cnblogs.com/nenya33/p/8079861.html 版權：本文版權歸作者和部落格園共有 
轉載：歡迎轉載，但須保留此段宣告，並在文章中給出原文連線；否則必究法律責任

==============================================我是分割線==============================================

DNN = Deep Neural Network

1. 領軍人物

 

2. 全連線神經網路 

輸入資料經過網路，執行一系列的操作後，找到輸出類概率，與真實標籤比較，計算出誤差值，然後用誤差計算梯度，之後梯度會告訴我們如何在反向傳播過程中更新權重。

BP演算法：

• 是一個用來求解目標函式關於多層網路權值梯度的反向傳播演算法。
• 求導的鏈式法則的具體應用。
• 指導機器如何從前一層獲取誤差而改變本層的內部引數，這些內部引數可以用於計算表示。 

3. 深層結構的啟發

（1）深度不夠，對於大的輸入，每個隱藏層的節點太多，泛化能力差

（2）人腦是深層結構

（3）認知過程似乎是深度的(人腦形成idea是層級的;人第一次學習簡單的concepts後會將其組合形成更抽象的表徵)

4.從深度上來看神經網路的進化史

CNN更易於訓練並且比全連線的神經網路的泛化效能更好，被計算機視覺團隊廣泛使用。

關於卷積層形象化的解釋：像一個方形手電筒，照亮影象上的每個畫素，找到影象中最相關的部分，然後做乘積、加和運算，最終輸出一個特徵圖，特徵圖表示的是從影象中學習到的特徵。在得到了特徵圖後，會用到非線性啟用函式，作用是使網路既能學習線性特徵，又能學習非線性特徵，用ReLU函式而不是其他函式的原因在於，能夠解決BP過程中梯度消失的問題。

關於池化層的解釋：假設有一個畫素矩陣，有很多數字0-255，以max pooling為例，它做的就是把這些數字劃分成小塊，從每個小塊中取出最大的畫素值，向前傳播，這樣得到更小的新的畫素矩陣，用於前向傳播，加速，減少了訓練的時間。

LeNet  1986 

 

conv-pooling-conv-pooling

AlexNet  2012  8層

 

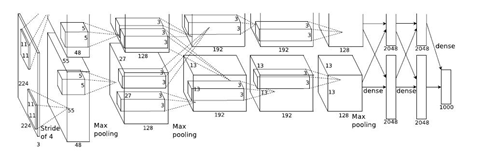
conv-pooling-conv-pooling-conv-conv-conv-pooling

VGG-Net  2014    16-19層

 

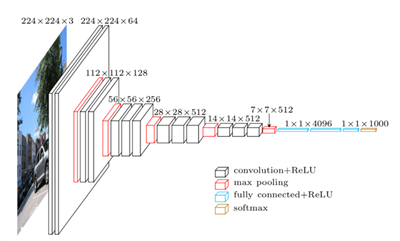
2convs- pooling-2convs-pooling-3convs-pooling-3convs-pooling-3convs-pooling

GoogLeNet   2014    22層

 

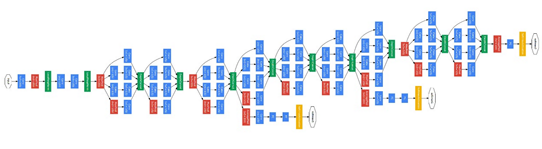
用更多的卷積，更深的網路可以得到更好的模型

ResNet   2015    152層

 

圖中為34層

歷屆ILSVRC比賽代表性模型的成績及其神經網路深度

 

參考

1. Deep learning. Yann LeCun, Yoshua Bengio& Geoffrey Hinton

Capsule

1. Who？

“神經網路之父”Geoffrey Hinton提出Capsule

 

2. Why？為什麼要提出Capsule

2017年8月17日，“神經網路之父”Geoffrey Hinton加拿大多倫多菲爾茲研究所開講，主題為《What is wrong with convolutional neural nets?》，指出了神經網路存在的問題。

在Hinton看來，標準神經網路存在如下問題：

（a）結構層次太少。只有神經元、層、網路三個層級；

（b）我們需要把每一層的神經元組成capsules，capsule可以做大量內部計算，然後輸出壓縮的結果。（靈感來自於大腦皮層中的微柱狀體mini-coulumn）

 

Capsule表示什麼呢？

（a）每個capsule表徵檢測型別的多維實體的例項化引數和存在性；

（b）例如，在視覺路徑中，capsule檢測物體或者部分物體的特定型別；

（c）一個capsule輸出兩部分：物體呈現出某種型別的概率；物體的廣義姿態，包括位置、方向、大小、形變、速率和顏色等。

Capsule的作用是同步過濾：

（a）典型的capsule接收底層capsule的多維預測向量，尋找緊密的預測群（可以理解為類別）；

（b）如果找到了一個緊密的群，capsule會輸出：這個型別存在的實體在這個domain（領域）的較高概率，以及這個簇的中心，這個中心就是那個實體的廣義姿態。

（c）善於過濾噪聲，因為高維一致性不會偶然發生。capsule比通常的神經元更好。

Yann LeCun和絕大多數人做物體識別的現有方式分為以下幾種：

（a）卷積網路使用多層的學習好的特徵檢測器（好）；

（b）在卷積網路中，特徵檢測器是區域性的，每種型別的檢測器被複制到整個空間中（好）；

（c）在卷積網路中，層次越高，特徵檢測器的空間域越大（好）；

（d） 特徵提取層與下采樣層交叉存取，下采樣層對同類型的相鄰特徵檢測器的輸出進行了池化（差）。

 

將複製的特徵檢測器的輸出結合的動機和原因是什麼？

（a）池化在每一層級帶來了少量的平移不變性：捨去了最活躍的特徵檢測器的精確位置；如果pool之間重疊地更多或者特徵對其他特徵的相對位置進行了編碼，可能沒什麼問題。

（b） 池化減少了特徵提取的下一層的輸入數量。這使得我們可以在下一層有更多特徵型別。

 

池化存在四個主要的爭論：

（a）池化與圖形感知心理學不切合。它並沒有解釋為什麼我們給物體安排內在的座標框架，以及有效的原因。

（b）池化解決了錯誤的問題。我們想要的是均等性而不是不變性，是解開而不是丟棄。

（c）池化未能利用潛在的線性結構。它沒有利用可完美處理影象中最大變動來源的自然線性流形。

（d）池化很不擅長處理動態路由。我們需要把輸入的每一部分路由到知道如何處理它的神經元上去。發現最佳的選路等同於解析影象。

……

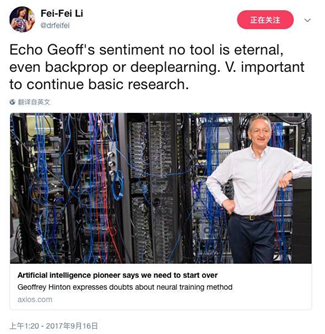
Hinton的這種精神也獲得了同行的肯定：工具都不是永恆的。

 

3. When？

2017年10月26日

事實上，在2011年Hinton在論文Transforming auto-encoders中引入過Capsule單元。

（Geoffrey E Hinton, Alex Krizhevsky, and Sida D Wang. Transforming auto-encoders. In Artificial Neural Networks and Machine Learning–ICANN 2011, pp. 44–51. Springer, 2011.）

4. Where？

5. What？Capsule究竟是什麼

來自論文摘要：

A capsule is a group of neurons whose activity vector represents the instantiation parameters of a specific type of entity such as an object or object part. We use the length of the activity vector to represent the probability that the entity exists and its orientation to represent the instantiation parameters. Active capsules at one level make predictions, via transformation matrices, for the instantiation parameters of higher-level capsules. When multiple predictions agree, a higher level capsule becomes active.

Capsule是一組神經元，它的啟用向量表示物體或者物體部分的特定型別的例項引數。用啟用向量的長度表示物體存在的概率，用方向表示例項引數。一個層級的啟用capsule做預測，通過變換矩陣得到更高層級capsule的例項引數。當多個預測一致時，更高層級的capsule被啟用。

6. How？從傳統神經網路角度解讀Capsule模型

（1）Capsule概念提出的背景

 

CNN可能會把右上方左圖也當做人臉，因為容易在pooling過程中丟失空間上的相關性，目標是得到右下方的結果。想要詳細瞭解capsule的提出背景，可以看Hinton的報告和論文。

實驗發現深度神經網路的另外一個缺點

（2）Capsule模型與傳統神經元的比較

  

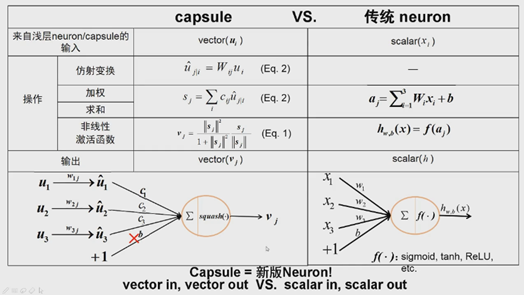
Capsule與傳統神經元對比，相似處很多：

在傳統神經元中，標量xi，加權求和得到aj。用非線性啟用函式，轉換得到神經元輸出，是個標量值，啟用函式可以選擇sigmoid、tanh和ReLU等，最終得到標量。

在Capsule中，ui是向量，矩陣的乘就是一個簡單的仿射變換，在傳統神經元中沒有，然後，對i維度做加權求和，傳統是對標量加權求和，Capsule是對向量加權求和得到向量。Squash函式是個非線性的函式，與傳統非線性對應，輸出是向量。

在論文第二部分核心內容：將標量輸入輸出擴充套件到向量輸入輸出。

新的神經元的引數有哪些呢？W和c。傳統方法中引數是用梯度方法更新，capsule中怎麼更新？

（3）引數更新演算法routing-by-agreement的分析

CNN用pooling做routing，capsule中則不同

 

實際上W用BP更新，Wij是8*16的矩陣，更新不多說；

C用另外一個原則更新，routing-by-agreement，cij是標量，重點看虛擬碼。

 

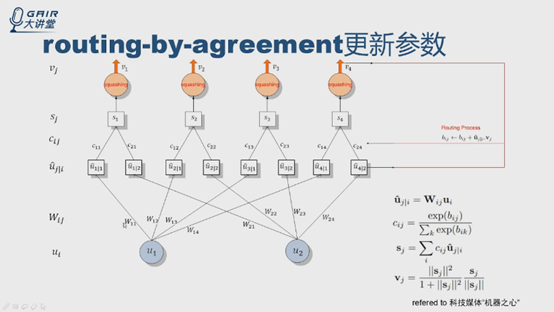
假設l層有兩個神經元，u1，u2，輸出是四個神經元v1v2v3v4。

從ui開始，用公式計算得到u4|1，u4|2.

 

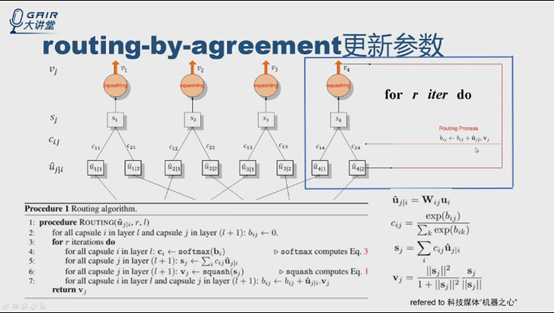
        根據虛擬碼中第4步和公式3，計算c14和c24，第5步得到S4，得到v4，根據虛擬碼第7步，得到新的b值。進行多輪迭代（r輪），更新c值，確定連線權重，輸出第r次迭代後的v4，輸入到網路的下一層。bij的更新與ui|i和vj有關，是標量積，實際上是個投票的過程， bij初始化為0。

       迭代輪數r是自己定義的，是個超引數，論文實驗表明r為3時效果最好。

 

在實驗中可以看到，routing還有很多相關的問題，效果還不是太理想。

實際上，總結起來，與簡單地新增層不同，capsule是在層中加巢狀層，新增一組神經元。

Siraj Raval總結為兩點： Layer-based squashing ：不是簡單地對每個神經元啟用，而是將這些神經元組成一個capsule，然後對整個capsule內的所有神經元做非線性啟用 Dynamic routing ：通過routing-by-agreement原則替換pooling

（4）CapNets模型

Capsule是個新的神經元，傳統的神經元可以構建網路，論文中第四部分給出了CapNets的模型，主要三層，不包括後面的重構模型，一層一層地看。

 

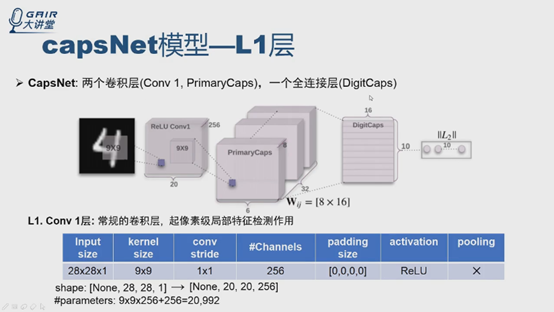
第一層是常規的卷積層，有什麼作用呢？為什麼不直接用capsule呢？（報告人認為可以擴充套件到capsule，需要實驗證明）還有兩層，PrimaryCaps層和DigitCaps層。

整個論文就是兩個卷積層，一個全連線層，Hinton把PrimaryCaps看做capsule的卷積層，把DigitCaps看做capsule的全連線層

PrimaryCaps層（在論文第四部分第一行）：

 

論文中說每個capsule是8D的，是8個卷積單元的結構，可以理解為8個通常意義上的卷積層。

整個L2層的輸入是20*20*256特徵圖，PrimaryCaps層卷積核是9*9，stride是2*2，通道是32，非線性函式是squashing函式，沒有用到routing演算法。怎麼理解呢？講兩種理解方式。

 

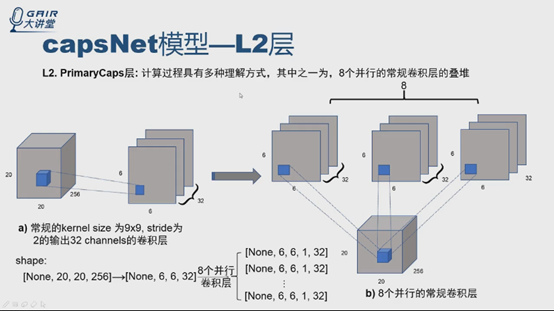
第一種：這一層可以看成8個並行的常規卷積層的疊堆，怎麼理解呢？

先看下a圖，從輸入的20*20*256，如果做常規的卷積層，與論文中提到的一樣，得到6*6*32，20-9=11，11/2=5.5，5.5+1=6.5，捨棄，最終得到6*6*32。維度的變化從20*20*256，得到6*6*32，並行地做8個卷積，擴充套件維度，加個1，就有8個張量了，怎麼做呢？把8個張量合併。

 

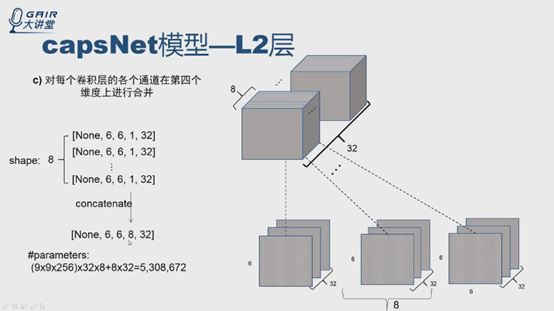
視覺化結果什麼樣?現在有8個6*6*32的，就是8堆，每一次從每一堆取其中一張6*6的特徵圖，共32張，就得到32個6*6*8，就與論文中模型一樣了。

 

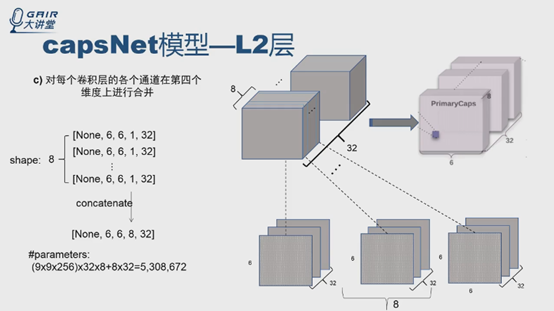
為什麼是並行，不是序列呢？可以有多種理解方式，這裡給出的是報告人最開始想到的一種方式，這種方式與論文中給出的PrimaryCaps層有32個通道，權重共享是6*6的描述對應起來了。

這種理解方式在計算時比較複雜，看另一種計算很簡單的理解方式。

 

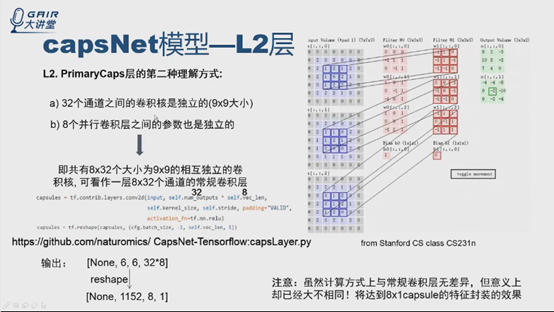
瞭解卷積概念的應該都清楚，32個通道就是有32個相互獨立的卷積核，8個並行的卷積層的單元相互獨立，就是說有8*32個相互獨立的卷積核，計算過程可以看成有8*32個通道的卷積層。那麼這一層的輸入input只用普通卷積（TensorFlow中conv2d）來計算，通道數直接就是self.num_outputs*self.vec_len=32*8，就實現了這一層的計算過程，之後reshape就得到下面1152*8*1的張量。8*1對應一個capsule的輸入，與論文一致。這個計算方式很簡單，與傳統卷積層無差別，但是意義已經不一樣了，因為在reshape之後，還加了一些層，在後續層的作用上，達到對8*1的特徵封裝的效果。 

DigitCaps層：

 

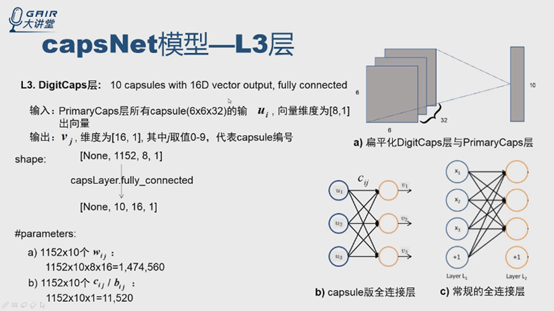
可以把每個capsule看成是神經元，輸出是向量，論文中說DigitCaps層是16D的向量，那麼可不可以把向量看成一個向量點？

理解方式就是，把向量扁平化，看成一個點，那麼這層的輸入PrimaryCaps實際上是6*6*32特徵圖，其中每個點是8*1的向量點，輸出是10個capsule，每個是10*1，也可以看成，每個神經元輸出一個向量點。下圖只畫了3個輸入三個輸出的圖，可以看做全連線，權重cij，輸出ui，是capsule版的全連線。與常規的區別在兩處：一是輸入輸出是向量，二是沒有偏置值。程式碼可以直接做capsLayer的fully_connected直接呼叫，從1152個capsule的輸入，得到10個capsule的輸出，每個capsule向量是16*1。引數個數計算方法，大家自己計算一下。

Q：有人問cij是矩陣嗎？

A：從每一條邊u1-v1來看cij是標量（公式2），對於整個過程可以寫成矩陣的形式。

 

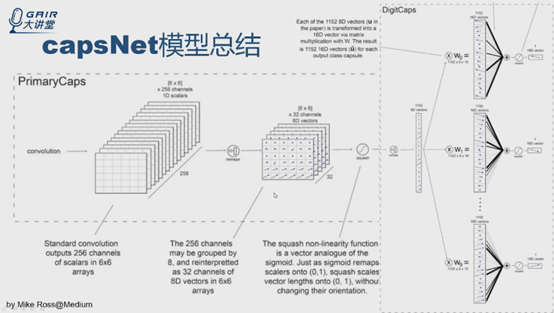
第一層就是常規卷積，就不說了。

PrimaryCaps層實際上就是一個卷積，就是一個32*8=256個通道，是個常規的卷積過程，直接做reshape，得到32個6*6*8，這個圖非常好，把每個8*1的向量表示成向量點，用箭頭表示，對特徵圖做非線性轉換squashing。這層結束。

DigitCaps層實際上就是capsule版的全連線層，先把6*6*32張量直接reshape成1152capsule，每個輸出是8D的向量點，後面輸出是10個capsule，每個capsule是16D的向量，權重是c。總結來說，capsNet是常規卷積層與capsule版全連線層的結合體。

 

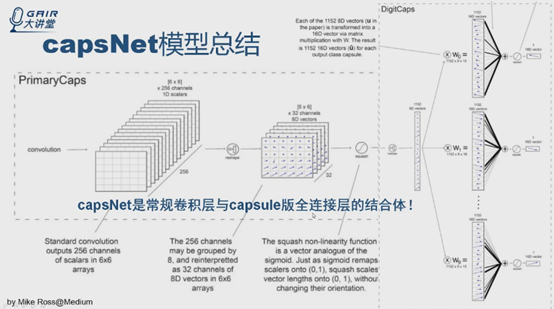
到這裡介紹完了論文第四部分模型的結構。接下來與傳統CNN /FC比較。

（5）CapsNet模型與卷積/全連線神經網路的比較

 

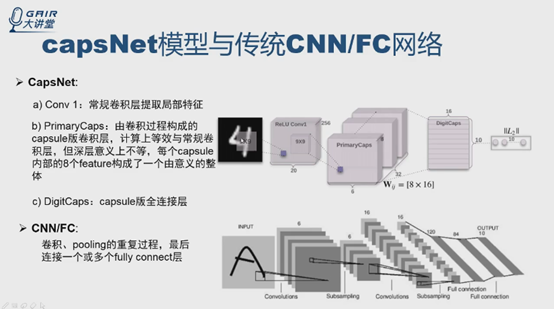
CapsNet共三層，先是常規卷積層，然後是capsule的卷積層，之後是capsule版的全連線層。

傳統CNN 也是這麼幹的，先卷積-pooling，再卷積-pooling，最後全連線層。能夠理解CNN中最後放全連線層的話，也能明白這裡也加全連線層的原因。理解相似之處。

另一個重要的是損失函式，論文中給出margin loss和重建loss

 

先說下重構網路，論文中說重構的主要目的是正則化，用的網路很簡單就是三層的全連線，不多說。

Margin loss函式才是主要的目的，這個函式在支援向量機中經常見到，自己查閱瞭解下。主要是限制vc長度的上下邊界，詳細內容自己查閱理解。

直接跳到實驗部分，論文中做了幾個有趣的實驗，按照論文的順序說

 

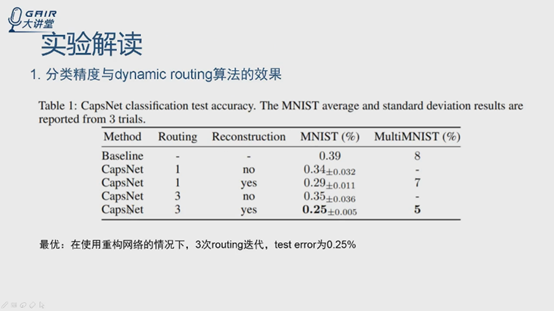
第一個做分類精度，驗證dynamic routing的效果，從論文給出的資料結果來看，第一列是模型，第二列是迭代次數，1和3，附錄有實驗證明，自己看，實驗表明3的時候效果最好，第三列表示是否加了重構網路，加了之後效果更好一點。但是事實上，自己做的實驗，就是github上的程式碼

 

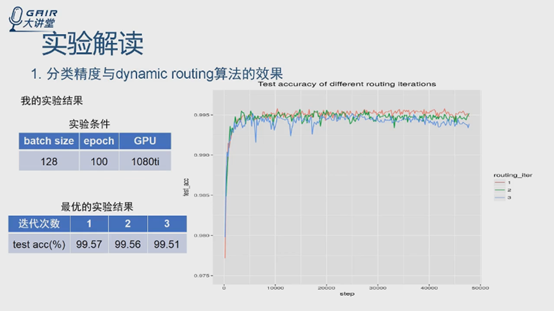
實驗條件儘量一致，也是128個batchsize，epoch 100，驗證routing迭代問題，取了1,2，3，下面是迭代次數，左側是精度。不知道是不是程式碼實現的問題，還是routing不是很好，主要時間消耗也在routing迭代，論文中一個很重要的改進點可以在routing上下手。

另一個實驗重構

 

說一個很有趣的問題，輸入是上面的一行，下面一行是重構出的，前三列竟然有去噪效果，尤其是8，可以好好地利用這個特點吧

還有一個實驗

 

之前說輸出的每個capsule是個向量，意義是什麼呢？實際上就是對實體的封裝，實體有不同的屬性，輸出的向量每個維度是否能明確表明實體的一個屬性，這個實驗就是證明這點。16維，在第一維上隨機加擾動，加0.05看結果，再加0.05，實驗中結果很好，每個維度能很好地表示手寫數字的一種屬性。

第四個實驗驗證做影象分割的能力

 

很重要的實驗，在一定程度上解決了CNN很難識別重疊影象的問題，輸入是包含兩個重疊數字的圖，輸出是能夠把重疊的數字區別出來，實驗結果表明具有非常強的畫素級分割的能力。這個特點可以做什麼問題呢？在處理公共場合的影象，行人多，有重疊，困難，CNN處理這個問題不是很理想，可以試試capsule

（6）討論：論文的貢獻及可改進之處

論文的主要貢獻

 

報告者認為引數更新方法與注意力機制有相似性

（7）核心演算法的程式碼剖析

核心程式碼是報告者自己實現的

地址在github上：https://github.com/naturomics/CapsNet-Tensorflow

 

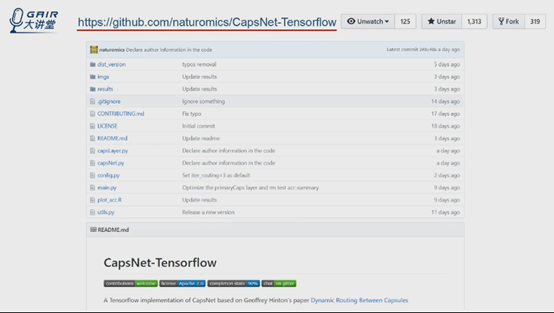
論文出來當天就出來，2天就跑起來了。

Capsnet檔案和capslayer

Q:訓練過程是怎樣的？BP和routing是交替進行的嗎？

A:Cij是在資料前向傳播更新的,看前面的圖

 

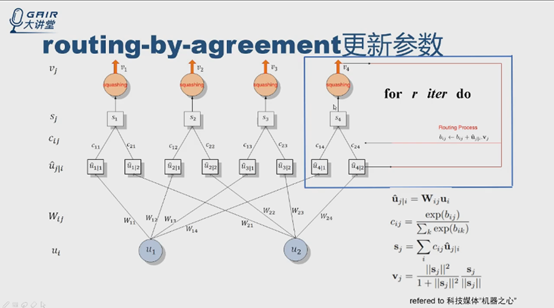
資料在前向計算時，在框內迭代更新cij，更新完才輸出v4，直到loss function，然後計算梯度，梯度返回來更新w，即c是在前向過程中計算的，w是在反向的過程BP中更新的。

Q:softmax是對第l層的i還是l+1層的j做的

A:k對應的是j的位置，即對圖中的這四個v做的

程式碼非常簡潔，只有四頁ppt

 

總結

正如Hinton在接受吳恩達採訪時所說的：

如果你的直覺很準，那你就應該堅持，最終必能有所成就；反過來你直覺不好，那堅不堅持也就無所謂了。反正你從直覺裡也找不到堅持它們的理由。

 

當Hinton在70歲時還在努力推翻自己積累了30年的學術成果時，我才知道什麼叫做生命力。

參考：

2. Hinton多倫多演講

有些圖片和內容是之前學習的時候記錄的，已經找不到出處了，如有侵權，請告訴我。如有錯誤，也請大家指出，謝謝閱讀。

2convs- pooling-2convs-pooling-3convs-pooling-3convs-pooling-3convs-pooling