圖片參考《演算法圖解》

      假如你是一個小偷，你有一個4磅的揹包，你可以偷下面物品，如何保證你能獲得最大價值？

        使用動態規劃，動態規劃是首先解決子問題然後再逐步解決大問題，對於揹包問題，先解決小揹包的問題，然後再解決原來的問題。

           每一個動態規劃的問題都是從網格開始的，揹包問題的網格如下面：

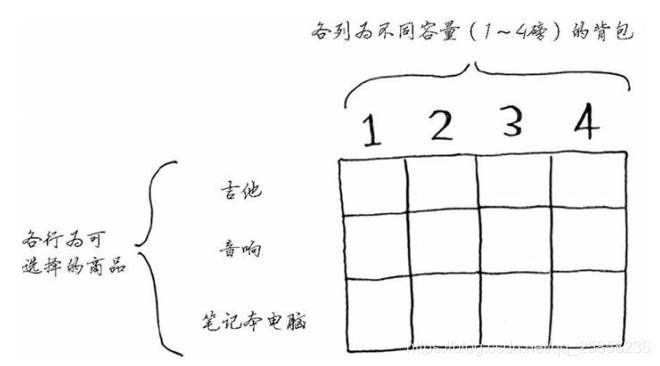
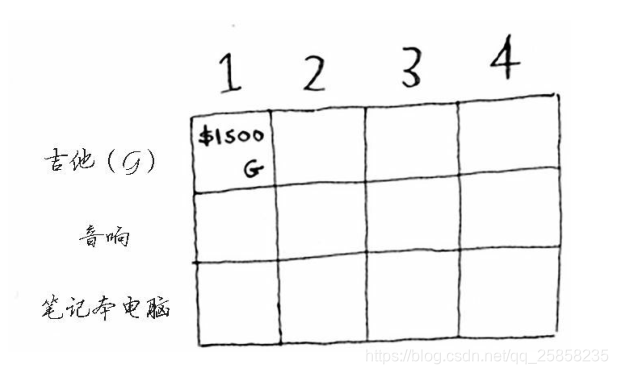
         首先是一件物品一件物品去放置，我們從吉他這一行開始。第一個單元格的質量為1磅，所以吉他的質量為1磅，可以放入，價值為1500元。

          我們繼續來看其他的格子，可以發現第2個格子也是完全足夠的，第3個，第4個同理，因為是第一行只能放吉他，所以都是1500。

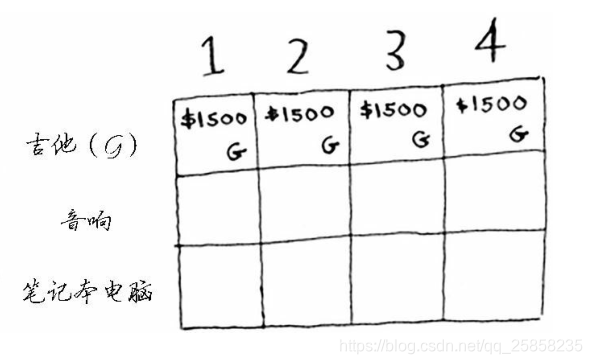
       繼續來看音響行，現在可以偷的東西有吉他(1磅)，有音響(4磅)。

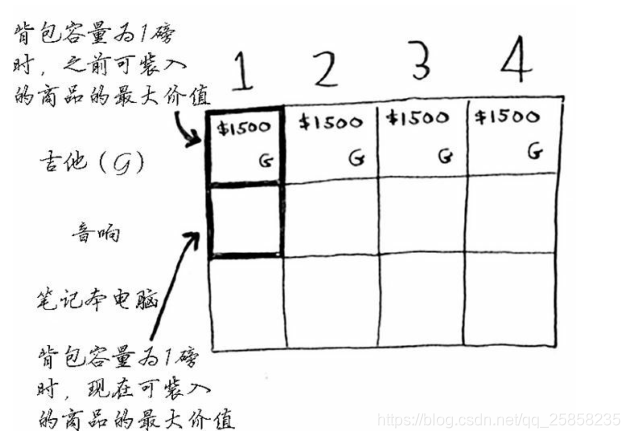
       看到音響行第一個格子，我們可以看出音響太重放不下去。所以當前最大值也就是之前一行的最大值，依然是1500

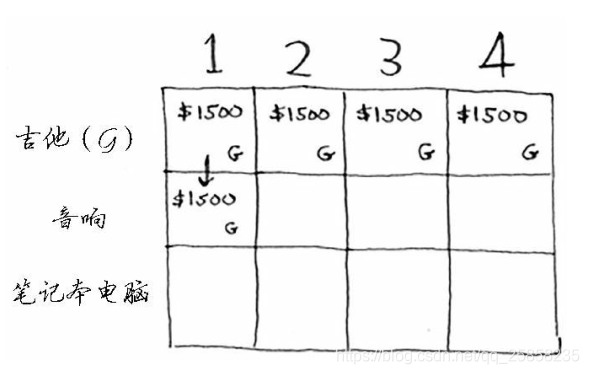
        所以類似往下面看，只有到了重量為4磅的格子的時候才放的下音響，而且價值比放吉他大，價格更新為3000

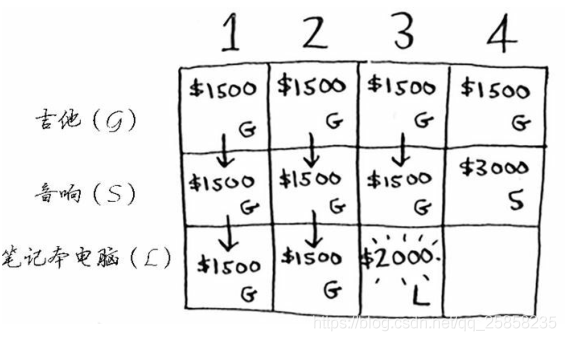
    同理我們看到最後的膝上型電腦這一行。

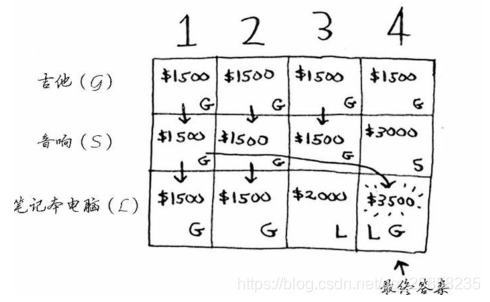
#include <iostream>
using namespace std;
//定義物品數量 
#define LENGTH 3 
//定義揹包容量 
#define CAPACITY 4 
void dynamic_pg(int weight[],int value[] ,int knapsack[][CAPACITY+1]){
	for(int i = 1 ; i < LENGTH+1 ; i ++){ //迴圈物品數量，從第一種物品開始 
		for (int j = 1; j< CAPACITY+1 ; j ++){//迴圈揹包容量，從揹包容量為1開始 
			if (j < weight[i])  
				knapsack[i][j] = knapsack[i-1][j];//如果當前物品容量大於當前揹包容量，就繼續使用原來的物品 
			else{
				knapsack[i][j]  = max(knapsack[i-1][j],//上一個單元格的value 
									  knapsack[i-1][j-weight[i]] + value[i]);//j-weight[i]：揹包容量減去當前物品剩餘的重量。value[i]當前物品的重量 
						//knapsack[i-1][j-weight[i]] 所以得到的就是揹包剩餘容量能放的最大價值，這裡就體現出就是首先解決子問題，然後再解決大問題 
			}
		cout << knapsack[i][j] <<' ';
		}
		cout << endl;
	}
}
int main (){
	int weight[LENGTH+1] = {0,1,4,3};//需要從陣列下標為1開始賦值 
	int value[LENGTH+1] = {0,1500,3000,2000};
	int knapsack[CAPACITY+1][CAPACITY+1] = {0};
	dynamic_pg(weight,value,knapsack);
	return 0;
}