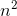目錄

題目

解題思路

程式碼

題目

題目描述

有Q只猴子要從第一棵樹到第n棵樹去，第i只猴子一次跳躍的最遠距離為Ki。如果它在第x棵樹，那它最遠可以跳到第x+Ki棵樹。如果第j棵樹的高度比第i棵樹高或相等，那麼它從第i棵樹直接跳到第j棵樹，它的勞累值會增加1。所有猴子一開始在第一棵樹，請問每隻猴子要跳到第n棵樹花費的勞累值最小。

輸入

第一行一個整數n，表示有n棵樹。（2<=n<=1000000），接下來第二行給出n個正整數D1，D2，……，Dn（1<=Di<=10^9）,其中Di表示第i棵樹的高度。第三行給出了一個整數Q（1<=Q<=25）,接下來Q行，給出了每隻猴子一次跳躍的最遠距離Ki(1<=Ki<=N-1)。

輸出

輸出Q行，每行一個整數，表示一隻猴子的最小的勞累值。

樣例輸入

9
4 6 3 6 3 7 2 6 5
2
2
5

樣例輸出

2
1

解題思路

可以看到，這裡所有的題都是dp，所以，這裡就只考慮dp怎麼實現正解。

可以看到，令dp[i] 是為到第i棵樹時前面最小的疲勞值，轉移方程可以很快地得到：dp[i] = min (dp[k] + (h[k] <= h[i]));

這裡的h[k] <= h[i] 也就是說如果第k棵樹比第i棵樹矮或相等的話就會加1（詳見題目）。

然後k的取值也是i - K[i] <= k < i，也就是往前列舉。或許會有人說了，這樣的時間複雜度不就是 O (

別慌別慌，這不是就到主題了嗎——用單調棧、佇列來優化dp。

我們可以用單調上升的佇列來儲存從i - K[i] ~ i 之間的最小值，把它賦給dp[i]，再把dp[i]放到合適的位置，不就萬事大吉了嗎!

當然，這裡還有一個小問題，將dp[i]放到合適的位置時，如果dp[i]大於了隊尾，那麼就直接放到它後面就行了；如果是小於，就一直到比它還小的元素後面；

可是如果是等於呢？

仔細想想可以想到，越高的樹是越有潛力的，在後面的作用更大。所以如果是隊尾的高度小於了該高度，那麼也直接踢掉，否則就加到後面去。

程式碼

#include <cstdio>
#include <deque>
#include <cstring>
using namespace std;
#define MAXN 1000000
#define INF 0x3f3f3f3f
 
int n, d[MAXN + 5], q, k[MAXN + 5], dp[MAXN + 5];
deque <int> D;
 
void Clear (){
    memset (dp, INF, sizeof (dp));
    D.clear ();
}
 
void read (int &x){
    x = 0;
    char c = getchar ();
    while (c < '0' || c > '9')
        c = getchar ();
    while (c >= '0' && c <= '9'){
        x = (x << 1) + (x << 3) + c - 48;
        c = getchar ();
    }
}

void print (int x){
    if (x < 0){
        putchar ('-');
        x = (~ x) + 1;
    }
    if (x / 10)
        print (x / 10);
    putchar (x % 10 + 48);
}

int main (){
    read (n);
    for (int i = 1; i <= n; i++)
        read (d[i]);
    read (q);
    for (int i = 1; i <= q; i++){
        read (k[i]);
        Clear ();
        dp[1] = 0;
        D.push_back (1);
        for (int j = 2; j <= n; j++){
            int Min = j - k[i];
            if (Min < 1)
                Min = 1;
            while (!D.empty ()){
                int x = D.front ();
                D.pop_front ();
                if (x < Min)
                    continue;
                else{
                    D.push_front (x);
                    break;
                }
            }
            int x = D.front ();
            dp[j] = dp[x];
            if (d[j] >= d[x])
                dp[j] ++;
            while (!D.empty ()){
                int x = D.back ();
                D.pop_back ();
                if (dp[x] > dp[j])
                    continue;
                else if (dp[x] == dp[j] && d[x] < d[j])
                    continue;
                else{
                    D.push_back (x);
                    break;
                }
            }
            D.push_back (j);
        }
        print (dp[n]);
        putchar ('\n');
    }
}