Java錯題集錦
這是個人做錯了的題目,記錄到該部落格,題目後面會附帶上網上搜索到的資料以及個人理解,如果有不正確的地方,請拍磚。
1、結構型模式中最體現擴充套件性的模式是()
A.裝飾模式
B.合成模式
C.橋接模式
D.介面卡
答案:A
解析:結構型模式是描述如何將類物件結合在一起,形成一個更大的結構,結構模式描述兩種不同的東西:類與類的例項。故可以分為類結構模式和物件結構模式。
在GoF設計模式中,結構型模式有:
介面卡模式 Adapter
介面卡模式是將一個類的介面轉換成客戶希望的另外一個介面。介面卡模式使得原本由於介面不相容而不能一起工作的那些類可以一起工作。
兩個成熟的類需要通訊,但是介面不同,由於開閉原則,我們不能去修改這兩個類的介面,所以就需要一個介面卡來完成銜接過程。
橋接模式 Bridge
橋接模式將抽象部分與它的實現部分分離,使它們都可以獨立地變化。它很好的支援了開閉原則和組合鋸和複用原則。實現系統可能有多角度分類,每一種分類都有可能變化,那麼就把這些多角度分離出來讓他們獨立變化,減少他們之間的耦合。
組合模式 Composite
組合模式將物件組合成樹形結構以表示部分-整體的層次結構,組合模式使得使用者對單個物件和組合物件的使用具有一致性。
裝飾模式 Decorator
裝飾模式動態地給一個物件新增一些額外的職責,就增加功能來說,它比生成子類更靈活。也可以這樣說,裝飾模式把複雜類中的核心職責和裝飾功能區分開了,這樣既簡化了複雜類,又去除了相關類中重複的裝飾邏輯。裝飾模式沒有通過繼承原有類來擴充套件功能,但卻達到了一樣的目的,而且比繼承更加靈活,所以可以說裝飾模式是繼承關係的一種替代方案。
外觀模式 Facade
觀模式為子系統中的一組介面提供了統一的介面,外觀模式定義了一個高層介面,這個介面使得這一子系統更加容易使用。
外觀模式中,客戶對各個具體的子系統是不瞭解的,所以對這些子系統進行了封裝,對外只提供了使用者所明白的單一而簡單的介面,使用者直接使用這個介面就可以完成操作,而不用去理睬具體的過程,而且子系統的變化不會影響到使用者,這樣就做到了資訊隱蔽。
享元模式 Flyweight
享元模式為運用共享技術有效的支援大量細粒度的物件。因為它可以通過共享大幅度地減少單個例項的數目,避免了大量非常相似類的開銷。.
享元模式是一個類別的多個物件共享這個類別的一個物件,而不是各自再例項化各自的物件。這樣就達到了節省記憶體的目的。
代理模式 Proxy
為其他物件提供一種代理,並由代理物件控制對原物件的引用,以間接控制對原物件的訪問。
2、下面程式碼的輸出是什麼?
public class Base
{
private String baseName = "base";
public Base()
{
callName();
}
public void callName()
{
System. out. println(baseName);
}
static class Sub extends Base
{
private String baseName = "sub";
public void callName()
{
System. out. println (baseName) ;
}
}
public static void main(String[] args)
{
Base b = new Sub();
}
}A.null
B.sub
C.base
答案:A
解析:首先要清楚物件的初始化過程:
- 父類靜態程式碼區和父類靜態成員
- 子類靜態程式碼區和子類靜態成員
- 父類非靜態程式碼區和普通成員
- 父類建構函式
- 子類非靜態程式碼區和普通成員
- 子類建構函式
此題中Base b = new Sub();語句建立Sub物件,並向上轉型為其父類Base型別,根據物件初始化的順序,父類、子類中都沒有靜態成員跟靜態程式碼塊,所以先給父類的成員baseName賦值,然後執行父類的構造器函式,父類的構造方法中呼叫了callName()方法,而子類重寫了該方法,所以這裡呼叫的是子類的callName()方法,子類的callName()方法方法輸出的是子類的baseName,而在這裡,初始化的過程還沒有執行到為baseName賦值的語句,所以baseName是null,結果輸出了null。
3、以下程式碼執行的結果是多少()?
public class Demo {
public static void main(String[] args) {
Collection<?>[] collections =
{new HashSet<String>(), new ArrayList<String>(), new HashMap<String, String>().values()};
Super subToSuper = new Sub();
for(Collection<?> collection: collections) {
System.out.println(subToSuper.getType(collection));
}
}
abstract static class Super {
public static String getType(Collection<?> collection) {
return “Super:collection”;
}
public static String getType(List<?> list) {
return “Super:list”;
}
public String getType(ArrayList<?> list) {
return “Super:arrayList”;
}
public static String getType(Set<?> set) {
return “Super:set”;
}
public String getType(HashSet<?> set) {
return “Super:hashSet”;
}
}
static class Sub extends Super {
public static String getType(Collection<?> collection) {
return "Sub"; }
}
}A. Sub:collection
Sub:collection
Sub:collection
B. Sub:hashSet
Sub:arrayList
Sub:collection
C. Super:collection
Super:collection
D. Super:hashSet
Super:arrayList
Super:collection
答案:C
解析:Sub繼承類Super,但是Sub類中的getType方法是靜態的,靜態方法是靜態繫結的,在編譯期間就確定了會呼叫哪個方法,而不是在執行期間根據具體物件的型別進行繫結(多型繫結),因為定義的變數型別是Super,所以在編譯期間就確定了呼叫父類的getType方法,而且傳入getType方法的引數是Collection型別,所以呼叫了父類的getType(Collection<?> collection)方法。
static方法可以被子類繼承,但是不能被子類重寫(覆蓋),可以被子類隱藏。(這裡意思是說如果父類裡有一個static方法,它的子類裡如果沒有對應的方法,那麼當子類物件呼叫這個方法時就會使用父類中的方法。而如果子類中定義了相同的方法,則會呼叫子類的中定義的方法。唯一的不同就是,當子類物件上轉型為父類物件時,不論子類中有沒有定義這個靜態方法,該物件都會使用父類中的靜態方法。因此這裡說靜態方法可以被隱藏而不能被覆蓋。這與子類隱藏父類中的成員變數是一樣的。隱藏和覆蓋的區別在於,子類物件轉換成父類物件後,能夠訪問父類被隱藏的變數和方法,而不能訪問父類被覆蓋的方法)。
4、Java類Demo中存在方法func0、func1、func2、func3和func4,請問該方法中,哪些是不合法的定義?( )
public class Demo {
float func0()
{
byte i=1;
return i;
}
float func1()
{
int i=1;
return;
}
float func2()
{
short i=2;
return i;
}
float func3()
{
long i=3;
return i;
}
float func4()
{
double i=4;
return i;
}
}
A.func1
B.func2
C.func3
D.func4
答案: A D
解析:資料型別的轉換,分為自動轉換和強制轉換。自動轉換是程式在執行過程中 “ 悄然 ” 進行的轉換,不需要使用者提前宣告,一般是從位數低的型別向位數高的型別轉換;強制型別轉換則必須在程式碼中宣告,轉換順序不受限制。
自動資料型別轉換
自動轉換按從低到高的順序轉換。不同型別資料間的優先關係如下:
低 ———————————————> 高
byte,short,char-> int -> long -> float -> double
運算中,不同型別的資料先轉化為同一型別,然後進行運算,轉換規則如下:
| 運算元1型別 | 運算元2型別 | 轉換後型別 |
|---|---|---|
| byte 、 short 、 char | int | int |
| byte 、 short 、 char 、 int | long | long |
| byte 、 short 、 char 、 int 、 long | float | float |
| byte 、 short 、 char 、 int 、 long 、 float | double | double |
強制資料型別轉換
強制轉換的格式是在需要轉型的資料前加上 “( )” ,然後在括號內加入需要轉化的資料型別。有的資料經過轉型運算後,精度會丟失,而有的會更加精確。
5、下面語句錯誤的是:
byte b1=1,b2=2,b3,b6,b8;
final byte b4=4,b5=6,b7;
b3=(b1+b2); /*語句1*/
b6=b4+b5; /*語句2*/
b8=(b1+b4); /*語句3*/
b7=(b2+b5); /*語句4*/
System.out.println(b3+b6);A.語句1
B.語句2
C.語句3
D.語句4
答案:A C D
解析:Java表示式轉型規則由低到高轉換:
- 所有的byte,short,char型的值將被提升為int型;
- 如果有一個運算元是long型,計算結果是long型;
- 如果有一個運算元是float型,計算結果是float型;
- 如果有一個運算元是double型,計算結果是double型;
- 被fianl修飾的變數不會自動改變型別,當2個final修飾相操作時,結果會根據左邊變數的型別而轉化。
語句1錯誤:b3=(b1+b2);
自動轉為int,所以正確寫法為b3=(byte)(b1+b2);或者將b3定義為int;
語句2正確:b6=b4+b5;
b4、b5為final型別,不會自動提升,所以和的型別視左邊變數型別而定,即b6可以是任意數值型別;
語句3錯誤:b8=(b1+b4);
雖然b4不會自動提升,但b1仍會自動提升,所以結果需要強轉,b8=(byte)(b1+b4);
語句4錯誤:b7=(b2+b5); 同上。
同時注意b7是final修飾,即只可賦值一次,便不可再改變。
6、 雜湊查詢中k個關鍵字具有同一雜湊值,若用線性探測法將這k個關鍵字對應的記錄存入雜湊表中,至少要進行( )次探測。
A.k
B.k+1
C.k(k+1)/2
D.1+k(k+1)/2
答案:C
解析:線性探測直接使用陣列來儲存資料。可以想象成一個停車問題,若當前車位已經有車,則你就繼續往前開,直到找到下一個為空的車位。
當碰撞發生時,直接檢測散列表中的下一位置。這樣線性探測可能發生三種結果:
- 命中–該位置的鍵和被查詢的鍵相同(填入,替換值)
- 未命中–鍵為空(該位置沒有鍵,直接填入)
- 繼續查詢–該位置的鍵和被查詢的鍵不同(再次探測)
線性探測容易產生“聚集”現象。當表中的第i、i+1、i+2的位置上已經儲存某些關鍵字,則下一次雜湊地址為i、i+1、i+2、i+3的關鍵字都將企圖填入到i+3的位置上,這種多個雜湊地址不同的關鍵字爭奪同一個後繼雜湊地址的現象稱為“聚集”。聚集對查詢效率有很大影響。
對於該題目:k個鍵衝突,第一個不衝突,直接填入陣列,算1次,第二個跟第一個衝突了,那麼需要填到第二個桶號,需要2次,……,第k個跟前面k-1個都產生衝突,然後填入陣列,需要k次,所以一共需要k(k+1)/2。
但是我看到了一樣的題目,答案是k(k-1)/2,這樣的答案是直接填入陣列時不算探測,所以是0 + 1 + 2 + … + k - 1,所以是k(k-1)/2。
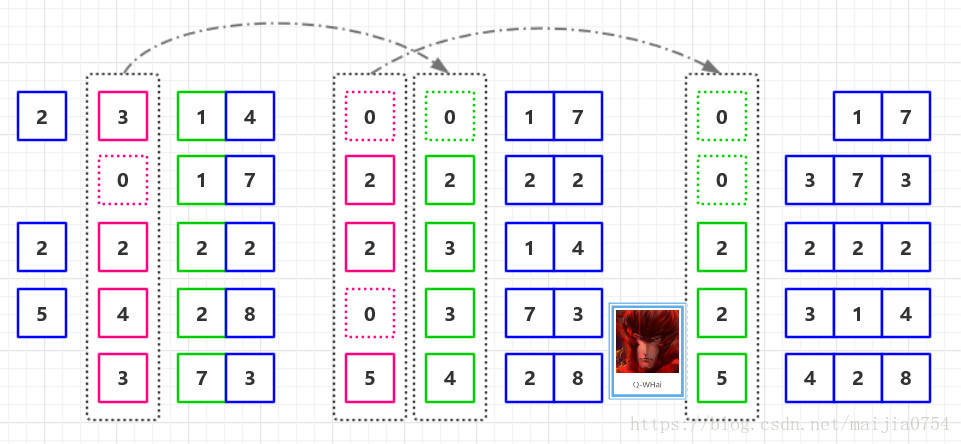
7、對{05,46,13,55,94,17,42}進行基數排序,一趟排序的結果是:
A.05,46,13,55,94,17,42
B.05,13,17,42,46,55,94
C.42,13,94,05,55,46,17
D.05,13,46,55,17,42,94
答案是:C
基數排序(radix sort)屬於“分配式排序”(distribution sort),又稱“桶子法”(bucket sort)或bin sort,顧名思義,它是透過鍵值的部份資訊,將要排序的元素分配至某些“桶”中,藉以達到排序的作用,基數排序法是屬於穩定性的排序。
先對個位進行排序,再到十位…
如圖(網上找來的):
所以上圖一趟排序的結果是42,13,94,05,55,46,17。
8、若一顆二叉樹的前序遍歷為a,e,b,d,c,後序遍歷為b,c,d,e,a,則根節點的孩子節點()
A.只有e
B.有e,b
C.有e,c
D.不確定
答案:A
解析:二叉樹是每個節點最多有兩個子樹的樹結構。
先序遍歷
首先訪問根,再先序遍歷左(右)子樹,最後先序遍歷右(左)子樹。
中序遍歷
首先中序遍歷左(右)子樹,再訪問根,最後中序遍歷右(左)子樹。
後序遍歷
首先後序遍歷左(右)子樹,再後序遍歷右(左)子樹,最後訪問根。
該題目中,前序遍歷為a,e,b,d,c,所以根節點為a。假設a有兩個子節點,由於前序遍歷中a的後面是e,所以e必定屬於a的左子樹中的節點。後序遍歷中a的前面緊挨著的是e,所以e必定是a右子樹的節點,相互矛盾,所以a只有一個孩子節點。而且在前序遍歷中a跟e是緊挨著的,所以e是a的子節點。
9、下面哪種情況會導致持久區jvm堆記憶體溢位?
A.迴圈上萬次的字串處理
B.在一段程式碼內申請上百M甚至上G的記憶體
C.使用CGLib技術直接操作位元組碼執行,生成大量的動態類
D.不斷建立物件
答案:C
簡單的來說 java的堆記憶體分為兩塊:permantspace(持久帶)和heap space。
持久帶中主要存放用於存放靜態型別資料,如 Java Class, Method 等,與垃圾收集器要收集的Java物件關係不大。
而heapspace分為年輕帶和年老帶 ,
年輕代的垃圾回收叫Young GC,年老代的垃圾回收叫Full GC。
在年輕代中經歷了N次(可配置)垃圾回收後仍然存活的物件,就會被複制到年老代中。因此,可以認為年老代中存放的都是一些生命週期較長的物件 。
年老代溢位原因有:迴圈上萬次的字串處理、建立上千萬個物件、在一段程式碼內申請上百M甚至上G的記憶體,既A B D選項。
持久代溢位原因:動態載入了大量Java類而導致溢位。
10、一棵124個葉結點的完全二叉樹,最多有()個結點
A.247
B.248
C.249
D.250
E.251
答案:B
解析:由於該樹是完全二叉樹,所以葉子節點只會存在於第h層跟第h-1層,假設第h-1層的葉子節點數為x,第h層的葉子結點數為y,那麼有x + y=124。根據完全二叉樹的性質,可以得知第h-1層的數量是2的N次方,那麼可以確定h-1層的節點數有64個,可以得到x + y/2(向上取整)=64,可以解得y=120或y=121,取y=121,可以有1 + 2 + 4 + 8 +16 +32 + 64 +121 = 248。(解題時也是這麼算的,居然算錯了,尷尬)。
看了別人的解析,根據完全二叉樹的性質:
n=n0+n1+n2
n:節點總數
n0:度為0的節點個數,也就是葉子節點
n1:度為1的節點個數,在完全二叉樹中值有0和1這兩種情況
n2:度為2的節點個數
又因為 n0=n2+1 所以n2=123,n1取較大的1
結論 n=n0+n1+n2=124+1+123=248
11、已知串S=′aaab′,其Next陣列值為()
A.0123
B.1123
C.1231
D.1211
答案:A
解析:Next陣列的解法:
next陣列的求解方法是:第一位的next值為0,第二位的next值為1,後面求解每一位的next值時,根據前一位進行比較。首先將前一位與其next值對應的內容進行比較,如果相等,則該位的next值就是前一位的next值加上1;如果不等,向前繼續尋找next值對應的內容來與前一位進行比較,直到找到某個位上內容的next值對應的內容與前一位相等為止,則這個位對應的值加上1即為需求的next值;如果找到第一位都沒有找到與前一位相等的內容,那麼需求的位上的next值即為1。
對於本題,求next值的過程:
前兩位:next陣列值前兩位一定為01,即aaab中的前兩位aa對應01,如上表中next第1,2位為0和1.其實這就可以選出答案了.
第三位:3a前面是2a(2a表示序號為2的a),2a的next陣列值為1,將2a和1a相比,兩者相同,都是a,則3a的next值為2a的next值加1,即2;
第四位:4b前3a的next為2,3a與2a相比,二者相同,則其next值為2a的next加1,為3.
結果為0123,選A
如果比較的時候碰到與前一位字元“不同”怎麼辦?那就以前一位的next值為序號,找到這個序號對應的字元,再進行比較,如果與之相同,就用這一位的next值+1,如果不同就繼續重複這個操作直到找到相同的字元為止。如果一直重複到第一位還找不到,則將所求位的next值置為1。
此種解法請看:https://blog.csdn.net/iamyvette/article/details/77433991
12、關於計數排序的敘述中正確的是( )
A.計數排序是一種基於比較的排序演算法
B.計數排序的時間複雜度為O(n+k)
C.計數排序的空間複雜度為 O(k)
D.計數演算法是原地排序演算法
答案:B C
計數排序:計數排序是一個非基於比較的排序演算法,該演算法於1954年由 Harold H. Seward 提出。它的優勢在於在對一定範圍內的整數排序時,它的複雜度為Ο(n+k)(其中k是整數的範圍),快於任何比較排序演算法。當然這是一種犧牲空間換取時間的做法,而且當O(k)>O(n*log(n))的時候其效率反而不如基於比較的排序(基於比較的排序的時間複雜度在理論上的下限是O(n*log(n)), 如歸併排序,堆排序)。
演算法思想:
計數排序對輸入的資料有附加的限制條件:
- 輸入的線性表的元素屬於有限偏序集S;
- 設輸入的線性表的長度為n,|S|=k(表示集合S中元素的總數目為k),則k=O(n)。
在這兩個條件下,計數排序的複雜性為O(n)。
計數排序的基本思想是對於給定的輸入序列中的每一個元素x,確定該序列中值小於x的元素的個數(此處並非比較各元素的大小,而是通過對元素值的計數和計數值的累加來確定)。一旦有了這個資訊,就可以將x直接存放到最終的輸出序列的正確位置上。例如,如果輸入序列中只有17個元素的值小於x的值,則x可以直接存放在輸出序列的第18個位置上。當然,如果有多個元素具有相同的值時,我們不能將這些元素放在輸出序列的同一個位置上,因此,上述方案還要作適當的修改。
演算法過程:
假設輸入的線性表L的長度為n,L=L1,L2,..,Ln;線性表的元素屬於有限偏序集S,|S|=k且k=O(n),S={S1,S2,..Sk};則計數排序可以描述如下:
1、掃描整個集合S,對每一個Si∈S,找到線上性表L中小於等於Si的元素的個數T(Si);
2、掃描整個線性表L,對L中的每一個元素Li,將Li放在輸出線性表的第T(Li)個位置上,並將T(Li)減1。