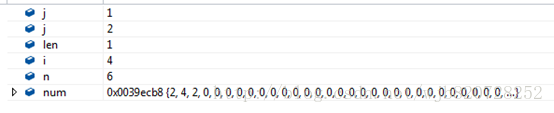大數(加、減、乘、除、低精度*大數)模板詳解(C++)
一、大數四個基本操作
首先,我們來了解什麼是大數,大數就是指用我們平常常見的高階語言(如:c 、c++)的基本資料型別的最大長度都裝不下的資料,例如(1234567899876543211234567896542132165465),這些只能用字元陣列(char[])或者字串(string)來處理,大數操作最基礎的四個操作就是:大數加法、大數減法、大數乘法、大數除法。下面我來詳細介紹下四個基礎操作的演算法。
在介紹演算法之前,先了解一下幾個C++中 string資料型別的用法。因為string類字元元素的訪問比C字串有所增強,優點十分多,用起來很方便,所以下面我大數模板全部是基於string來作為基礎資料型別。
String 優點如下(相對C)
1)string可以像C的字串陣列一樣用下標來直接訪問索引值對於的字元。
string str=”123456789123123” //初始化一個字串
str[i] //返回str中索引i處字元的引用,不查是否出界
str.at(i) //返回str中索引i處字元的引用,查是否出界
2)string過載了一些運算子,特別注意當目標串較小,無法容納新的字串,系統會自動分配更多的空間給目標串,不必顧慮出界:
3)string字串之間的賦值不再需要像C那樣移動陣列或者用strcpy()等函式輔助,string類可以直接賦值:
str1=str2; //str1成為str2的程式碼
str1+=str2; //str2的字元資料連線到str1的尾部
str1+str2; //返回一個字串,它將str2和str1連線起來
4)string字串之間的比較也不需要用strcmp()等函式來比較,可以直接用<>==
str1==str2; str1!=str2; //比較串是否相等,返回布林值
str1<str2; str1>str2; //基於字典序的比較,返回布林值
str1<=str2;
5) string字串還有一個標準且強大的STL庫,裡面提供了許多非常便利有用的輔助函式,如 str. erase ()函式(詳細介紹這個,因為下面演算法經常利用到)
erase函式的原型如下:
(1)string& erase ( size_tpos = 0, size_t n = npos );(常用)
作用:從下標size_t pos開始,去掉size_t n個字元
例子:str=”023543”
用法:str.erase(0,1);
結果:str=“23543”
(2)iterator erase ( iteratorposition );
作用:去掉一個下標為:position的字元
例子:str=”023543”
用法:str.erase(0);
結果:str=“23543”
(3)iterator erase ( iteratorfirst, iterator last );
作用:刪除從first到last之間的字元(first和last都是迭代器)
好了,瞭解string到這裡也差不多了。接下來就是演算法分析
一、大數加法
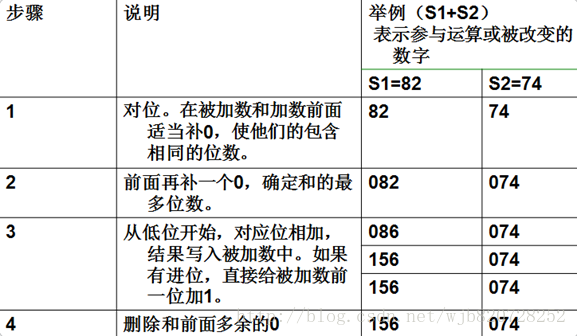
原理:首先我們要對字串進行初始化處理,就是給它們前面補上一個‘0’,防止有進位,如果沒有進位我們最後可以用erase()函式將其刪掉,然後直接對字串進行操作,從字串尾開始操作,往回對應相加,如果相加的結果>10,那麼前一個字元就要加上當前字元的進位,當前字元就只保留結果個位數
下面是圖解:
程式碼如下
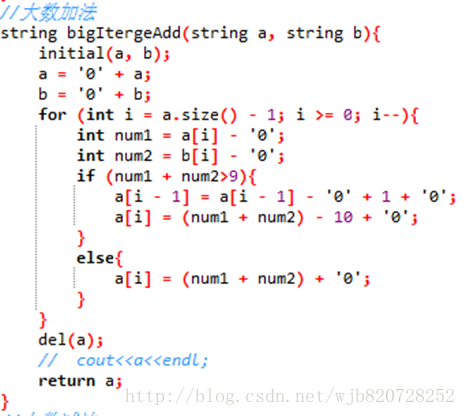
二、大數減法
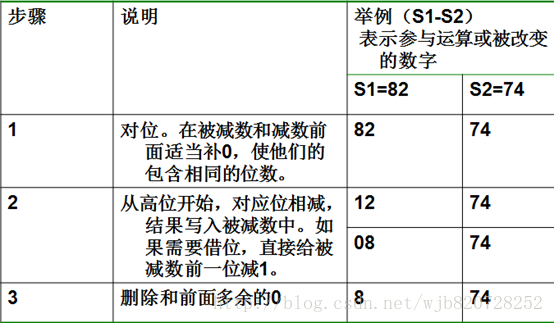
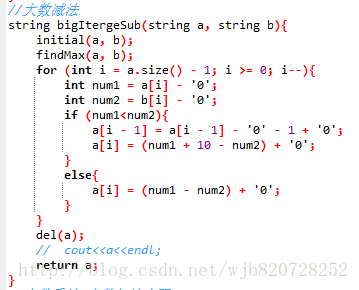
原理:減法操作和加法操作類似,首先先初始化,保持輸入都是大數減小數,然後從低位開始對應相減,不夠減就從借位減一。
圖解:程式碼如下
三、大數乘法
原理:乘法的主要思想是把乘法轉化為加法進行運算。
例子(12345*24)首先用相對小的大數(24)作為迴圈分割,4和 20,個位數4代表著4個123456相加。
12345*4=12345+12345+12345+12345
20代表著20個12345相加,也就是2個123450相加
12345*20=123450+123450
最終結果就是4個12345加上2個123450
12345*24=12345+12345+12345+12345+123450+123450
程式碼如下:

不明白?
我帶大家走一遍Debug,看一下資料的變化
首先初始化:
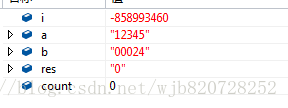
迴圈加上4次加上12345後結果res=49380
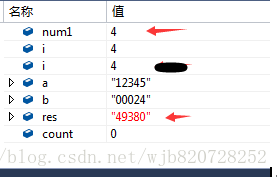
重複,迴圈2次加上123450,res=296280
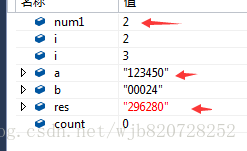
最終結果
四、大數除法
原理:首先想到的是運用大數減法,例如144 / 12,就是迴圈利用大數減法144-12,減一次就用大數加法加1,最終結束迴圈的條件是被減數小於減數。這個方法實現起來簡單,邏輯直觀,但是效率明顯不夠高,不信可以試一試(978973548932486564654654654654654654654564564564654532165454654 /2)
這個運用上面的方法會編譯器會直接卡死。其實呢,上面的只要進行優化一下就可以AC了。怎麼優化呢?
這樣,首先我們可以直接將減數擴充套件到剛剛好比被減數少一位(用‘0’擴充套件,就是乘於10,例如這裡剛好是擴大10倍)然後再大數相減,減一次就用大數加法加起來(這裡是加10),迴圈操作,同樣,迴圈結束條件也是被減數小於減數,這樣可以避免迴圈減一個小數的尷尬。
程式碼:

不明白?
下面走一遍debug,看一下資料變化
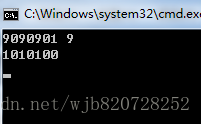
測試樣例(9090901 / 9)
第一步:擴充套件減數,在這裡減數從9擴充套件為900000,相當於*100000
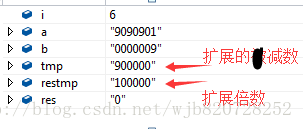
第二步:接著迴圈相減直至被減數小於擴充套件的減數即(a<tmp)結束,此時也迴圈大數相加加上了對應的擴充套件倍數就是結果(res)
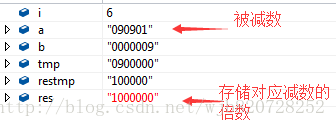
由於被減數(a=90901)還是大於減數(b=9),迴圈繼續
此時被減數(a=90901)小於擴充套件的除數(tmp=900000)了,需要將擴充套件的除數變小(這裡將它縮小10倍,即tmp=90000)圖如下:
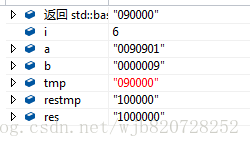
然後重複第二步的操作,直至被減數小於減數即(a<b)結束。

最終結果:
二、低精度*大數:
低精度*大數例如階乘(N!),1000!將會是一個非常大的數,用我們的基本資料型別是無法裝下的,1*2*3*4*·······*10000
當然這利用我們前一小節所說的大數乘法完成該功能也可以,但是還有一種專門用來處理這種情況的方法,就是利用一個數組來儲存每一位的字元。
例如:
5的階乘在數組裡面就是:
|
3 |
0 |
2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
6的階乘在數組裡面就是:
|
3 |
0 |
2 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
7的階乘在數組裡面就是:
|
4 |
0 |
4 |
0 |
5 |
0 |
0 |
0 |
0 |
發現嗎?
陣列的第一個元素其實就是表示當前結果的位數,其他元素就是結果的每一位數
5!=120
6!=720
7!=5040
那其中是如何實現的呢
程式碼如下:
首先使用一個數組num[50000]來儲存結果,將其初始化為0,num[0]=1,num[1]=1
這裡設定num[1]=1是因為階乘的原因,因為0的階乘還是1;
文字表達水平有限,原理還是看我debug走一遍更好理解
測試樣例是6的階乘(測試樣例太大不好講解)
做好初始化工作:i=1;[結果]res=1
第一步判斷num[0]此時的結果有多少位,再迴圈分別每位乘以i(第一輪i=1)
迴圈後陣列沒有變化
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
第二輪迴圈開始:i此時為2res*2 [注意,這裡*2是指結果的每一位乘以2] res=2
陣列變化
|
1 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
第三輪迴圈開始:i=3,res*3
陣列變化
|
1 |
6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
第四輪迴圈開始: i=4,res*4
注意這裡出現了24,沒錯,就是6*4=24,24>10了,此時就要進位,向後進位,原位置保持個位數,num[0]就要加多一位了,代表這結果的位數
陣列變化
|
2 |
4 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
第五輪迴圈開始: i=5,res*5

每位分別乘以5,4*5=202*5=10
再迴圈分割進位
陣列變化
|
3 |
0 |
2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
第六輪迴圈開始: i=6,res*6
同樣,每一位都分別乘以6
即:0*6=0 2*6 =12 1*6=6
掃描有大於10的進行進位拆分
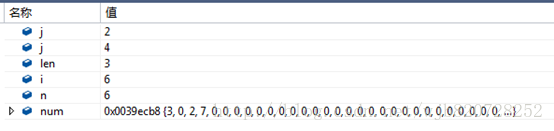
陣列變化
|
3 |
0 |
2 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
結束迴圈
最終:模板程式碼如下
#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
//初始化
void initial(string &a, string &b){
while (a.size()<b.size())a = '0' + a;
while (b.size()<a.size())b = '0' + b;
}
//列印
void print(string &a, string &b){
cout << a << endl;
cout << b << endl;
}
//找出最大的字串
void findMax(string &a, string &b){
string tmp;
if (a<b){
tmp = b;
b = a;
a = tmp;
}
}
//刪除第一個字元'0'
bool del(string &a){
if (a[0] == '0'){
a.erase(0, 1);
return true;
}
else
return false;
}
//刪除前面所有的 0
void delAllZroe(string &a){
while (del(a)){
del(a);
};
}
//大數加法
string bigItergeAdd(string a, string b){
initial(a, b);
a = '0' + a;
b = '0' + b;
for (int i = a.size() - 1; i >= 0; i--){
int num1 = a[i] - '0';
int num2 = b[i] - '0';
if (num1 + num2>9){
a[i - 1] = a[i - 1] - '0' + 1 + '0';
a[i] = (num1 + num2) - 10 + '0';
}
else{
a[i] = (num1 + num2) + '0';
}
}
del(a);
// cout<<a<<endl;
return a;
}
//大數減法
string bigItergeSub(string a, string b){
initial(a, b);
findMax(a, b);
for (int i = a.size() - 1; i >= 0; i--){
int num1 = a[i] - '0';
int num2 = b[i] - '0';
if (num1<num2){
a[i - 1] = a[i - 1] - '0' - 1 + '0';
a[i] = (num1 + 10 - num2) + '0';
}
else{
a[i] = (num1 - num2) + '0';
}
}
del(a);
// cout<<a<<endl;
return a;
}
//大數乘法(大數加法實現)
void bigItergeMul(string a, string b){
delAllZroe(a);
delAllZroe(b);
if (a == "" || b == ""){ printf("0\n"); return; }
initial(a, b);
findMax(a, b);
string res = "0";
int count = 0;
delAllZroe(b);
for (int i = b.size() - 1; i >= 0; i--){
int num1 = b[i] - '0';
if (i != b.size() - 1) a = a + '0';
for (int i = 1; i <= num1; i++){
res = bigItergeAdd(res, a);
}
}
delAllZroe(res);
cout << res << endl;
}
//大數除法
void bigItergeDiv(string a, string b){
initial(a, b);
if (a<b){ cout << "0" << endl; return; }
delAllZroe(b);
string res = "0";
string restmp = "1";
string tmp = b;
for (int i = 1; i<(a.size() - b.size()); i++){
tmp += '0';
restmp += '0';
}
initial(a, b);
while (a >= b){
initial(a, tmp);
if (a >= tmp){
a = bigItergeSub(a, tmp);
res = bigItergeAdd(res, restmp);
}
else{
tmp.erase(tmp.size() - 1);
restmp.erase(restmp.size() - 1);
initial(a, tmp);
if (a >= tmp){
a = bigItergeSub(a, tmp);
res = bigItergeAdd(res, restmp);
}
}
initial(a, b);
}
cout << res << endl;
}
//階乘(0~10000)【實際是低精度 乘於(*) 大數 例如:1000 *32132156465465321】
void factorial(int n){
int num[50000];
memset(num, 0, sizeof(num));
num[0] = 1;
num[1] = 1;
for (int i = 1; i <= n; i++){
int len = num[0];
for (int j = 1; j <= len; j++){
num[j] *= i;
}
for (int j = 1; j <= num[0]; j++){
if (num[j]>9){
num[j + 1] += num[j] / 10;
num[j] %= 10;
}
if (num[num[0] + 1] != 0)num[0]++;
}
}
for (int i = num[0]; i>0; i--){
printf("%d", num[i]);
}
printf("\n");
}
int main(){
string a, b;
while (cin >> a >> b){
// bigItergeAdd(a,b);
// bigItergeSub(a,b);
bigItergeMul(a,b);
// bigItergeDiv(a, b);
}
// int n;
// while(scanf("%d",&n)!=EOF){
// factorial(n);
// }
return 0;
}以上的模板已經在acm.hdu.edu.cn和openjudge.cn上測試AC
大數加法
http://bailian.openjudge.cn/practice/1000/
這題在輸入做了手腳,輸入0,也要輸出0,WA了好幾次
大數減法
大數乘法
這道題目特坑,竟然在輸入做手腳,測試樣例會輸入一串00000000000000
或者 000000000001 * 000000000000001等等,在這上面WA了好幾次
大數除法
低精度*大數(N!)階乘
這些都是一些非常基礎的題目,一眼就看出是大數的運用,但實際運用上,大數只是作為解題的一個橋段,作為一個契機,例如前一篇文章
sicily1029Rabbit中大OJ解題報告
http://blog.csdn.net/wjb820728252/article/details/60583288