PP and QQ

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 510    Accepted Submission(s): 256

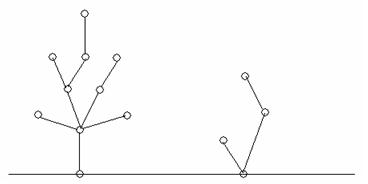
Problem Description PP and QQ were playing games at Christmas Eve. They drew some Christmas trees on a paper: 



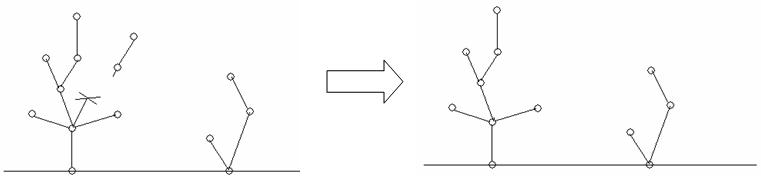
Then they took turns to cut a branch of a tree, and removed the part of the tree which had already not connected with the root. A step shows as follows: 

PP always moved first. 
PP and QQ took turns (PP was always the first person to move), to cut an edge in the graph, and removed the part of the tree that no longer connected to the root. The person who cannot make a move won the game. 
Your job is to decide who will finally win the game if both of them use the best strategy.  Input The input file contains multiply test cases.
The first line of each test case is an integer N (N<100), which represents the number of sub-trees. The following lines show the structure of the trees. The first line of the description of a tree is the number of the nodes m (m<100). The nodes of a tree are numbered from 1 to m. Each of following lines contains 2 integers a and b representing an edge <a, b>. Node 1 is always the root.  Output For each test case, output the name of the winner. Sample Input 2 2 1 2 2 1 2 1 2 1 2 Sample Output PP QQ Author alpc27

 1 #include<cstdio>
 2 #include<cstdlib>
 3 #include<cstring>
 4 #include<iostream>
 5 #include<algorithm>
 6
 
 using namespace std;
 7 #define Maxn 110
 8 
 9 struct node
10 {
11     int x,y,next;
12 }t[Maxn*2];
13 int first[Maxn],len;
14 
15 void ins(int x,int y)
16 {
17     t[++len].x=x;t[len].y=y;
18     t[len].next=first[x];first[x]=len;
19 }
20 
21 int dfs(int x,int f)
22 {
23     int ans=0;
24     for(int i=first[x];i;i=t[i].next) if(t[i].y!=f)
25     {
26         ans^=(dfs(t[i].y,t[i].x)+1);
27     }
28     return ans;
29 }
30 
31 int main()
32 {
33     int T;
34     while(scanf("%d",&T)!=EOF)
35     {
36         int ans=0;
37         bool ok=0;
38         while(T--)
39         {
40             int n;
41             scanf("%d",&n);
42             len=0;
43             for(int i=1;i<=n;i++) first[i]=0;
44             for(int i=1;i<n;i++)
45             {
46                 int x,y;
47                 scanf("%d%d",&x,&y);
48                 ins(x,y);ins(y,x);
49             }
50             int nw=dfs(1,0);
51             if(nw>1) ok=1;ans^=nw;
52         }
53         if((!ans&&!ok)||(ans&&ok)) printf("PP\n");
54         else printf("QQ\n");
55     }
56     return 0;
57 }

2017-04-27 17:11:55