本次用Python實現邏輯迴歸演算法，邏輯迴歸是應用非常廣泛的一個分類及其學習演算法，它將資料擬合到一個logit函式中，從而完成對事件發生的概率進行預測。

本次學習筆記主要參考了《Python進行資料分析與挖掘實踐》和作者@寒小陽的部落格，地址如下：http://blog.csdn.net/yaoqiang2011/article/details/49123419。

第一步，首先引入本次程式需要用的Python依賴庫：

import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

from scipy.optimize import minimize

from sklearn.preprocessing import PolynomialFeatures

pd.set_option('display.notebook_repr_html', False)
pd.set_option('display.max_columns', None)
pd.set_option('display.max_rows', 150)
pd.set_option('display.max_seq_items', None)
 
#%config InlineBackend.figure_formats = {'pdf',}
%matplotlib inline

import seaborn as sns
sns.set_context('notebook')
sns.set_style('white')
 

接下來開始定義loaddata、plotdata兩個函式，功能分別是讀取並顯示前六行資料，然後對樣本資料進行標引，這裡設定了五個引數，分別傳入資料，x,y標籤，資料的正負分類。

def loaddata(file, delimeter):
    data = np.loadtxt(file, delimiter=delimeter)
    print('Dimensions: ',data.shape)
    print(data[1:6,:])
    return(data)

def plotData(data, label_x, label_y, label_pos, label_neg, axes=None):
    # 獲得正負樣本的下標(即哪些是正樣本，哪些是負樣本)
    neg = data[:,2] == 0
    pos = data[:,2] == 1
    
    if axes == None:
        axes = plt.gca()
    axes.scatter(data[pos][:,0], data[pos][:,1], marker='+', c='k', s=60, linewidth=2, label=label_pos)
    axes.scatter(data[neg][:,0], data[neg][:,1], c='y', s=60, label=label_neg)
    axes.set_xlabel(label_x)
    axes.set_ylabel(label_y)
    axes.legend(frameon= True, fancybox = True);
 

呼叫loaddata方法：

data = loaddata('data1.txt', ',')

('Dimensions: ', (100, 3))
[[ 30.28671077  43.89499752   0.        ]
 [ 35.84740877  72.90219803   0.        ]
 [ 60.18259939  86.3085521    1.        ]
 [ 79.03273605  75.34437644   1.        ]
 [ 45.08327748  56.31637178   0.        ]]

對兩類資料進行分類並定義形狀。

X = np.c_[np.ones((data.shape[0],1)), data[:,0:2]]
y = np.c_[data[:,2]]
 

呼叫plotdata方法並傳入引數

plotData(data, 'Exam 1 score', 'Exam 2 score', 'Pass', 'Fail')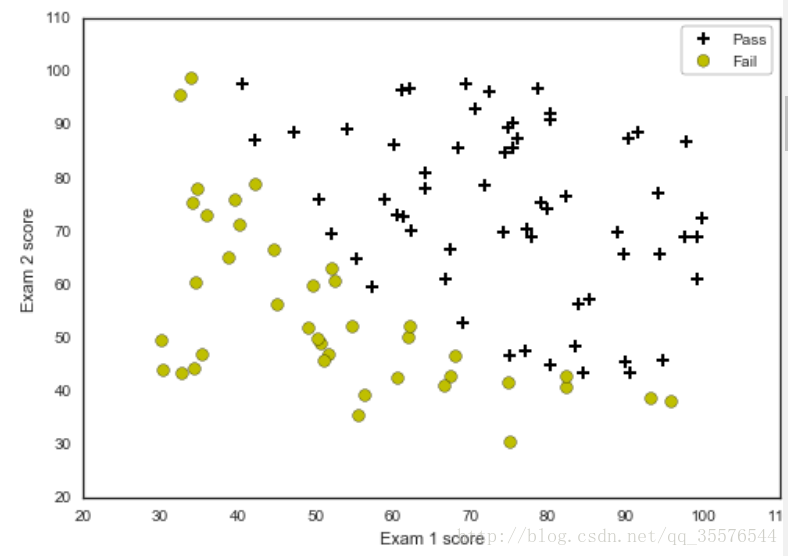

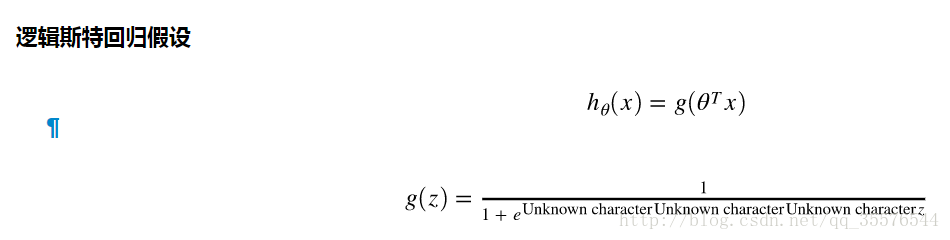
#定義sigmoid函式
def sigmoid(z):
    return(1 / (1 + np.exp(-z)))

#定義損失函式
def costFunction(theta, X, y):
    m = y.size
    h = sigmoid(X.dot(theta))
    
    J = -1.0*(1.0/m)*(np.log(h).T.dot(y)+np.log(1-h).T.dot(1-y))
               
    if np.isnan(J[0]):
        return(np.inf)
    return J[0]

#求解梯度
def gradient(theta, X, y):
    m = y.size
    h = sigmoid(X.dot(theta.reshape(-1,1)))
    grad =(1.0/m)*X.T.dot(h-y)
    return(grad.flatten())

initial_theta = np.zeros(X.shape[1])
cost = costFunction(initial_theta, X, y)
grad = gradient(initial_theta, X, y)
print('Cost: \n', cost)
print('Grad: \n', grad)

('Cost: \n', 0.69314718055994518)
('Grad: \n', array([ -0.1       , -12.00921659, -11.26284221]))

#最小化損失函式

res = minimize(costFunction, initial_theta, args=(X,y), jac=gradient, options={'maxiter':400})

res

   status: 0
  success: True
     njev: 28
     nfev: 28
 hess_inv: array([[  3.24739469e+03,  -2.59380769e+01,  -2.63469561e+01],
       [ -2.59380769e+01,   2.21449124e-01,   1.97772068e-01],
       [ -2.63469561e+01,   1.97772068e-01,   2.29018831e-01]])
      fun: 0.20349770158944075
        x: array([-25.16133401,   0.20623172,   0.2014716 ])
  message: 'Optimization terminated successfully.'
      jac: array([ -2.73305312e-10,   1.43144026e-07,  -1.58965802e-07])

def predict(theta, X, threshold=0.5):
    p = sigmoid(X.dot(theta.T)) >= threshold
    return(p.astype('int'))

plt.scatter(45, 85, s=60, c='r', marker='v', label='(45, 85)')
plotData(data, 'Exam 1 score', 'Exam 2 score', 'Admitted', 'Not admitted')
x1_min, x1_max = X[:,1].min(), X[:,1].max(),
x2_min, x2_max = X[:,2].min(), X[:,2].max(),
xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max), np.linspace(x2_min, x2_max))
h = sigmoid(np.c_[np.ones((xx1.ravel().shape[0],1)), xx1.ravel(), xx2.ravel()].dot(res.x))
h = h.reshape(xx1.shape)
plt.contour(xx1, xx2, h, [0.5], linewidths=1, colors='b');

data2 = loaddata('data2.txt', ',')

('Dimensions: ', (118, 3))
[[-0.092742  0.68494   1.      ]
 [-0.21371   0.69225   1.      ]
 [-0.375     0.50219   1.      ]
 [-0.51325   0.46564   1.      ]
 [-0.52477   0.2098    1.      ]]

# 拿到X和y
y = np.c_[data2[:,2]]
X = data2[:,0:2]

# 畫個圖
plotData(data2, 'Microchip Test 1', 'Microchip Test 2', 'y = 1', 'y = 0')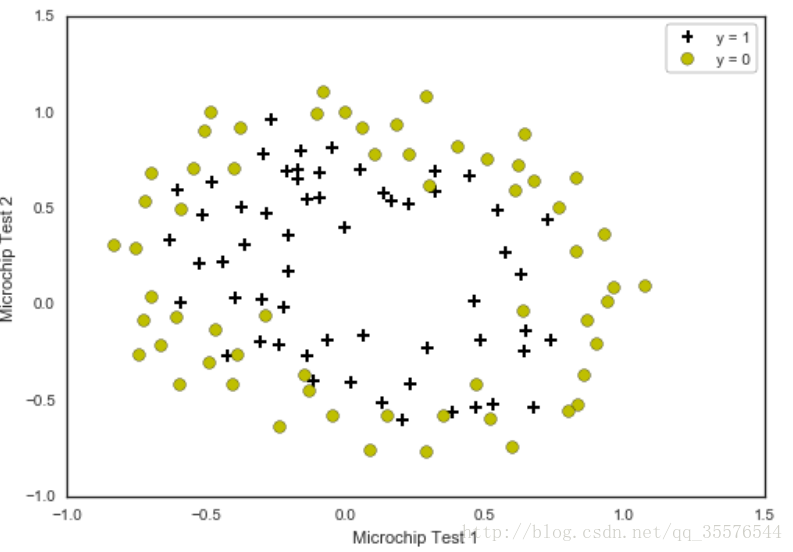

# 定義損失函式
def costFunctionReg(theta, reg, *args):
    m = y.size
    h = sigmoid(XX.dot(theta))
    
    J = -1.0*(1.0/m)*(np.log(h).T.dot(y)+np.log(1-h).T.dot(1-y)) + (reg/(2.0*m))*np.sum(np.square(theta[1:]))
    
    if np.isnan(J[0]):
        return(np.inf)
    return(J[0])

def gradientReg(theta, reg, *args):
    m = y.size
    h = sigmoid(XX.dot(theta.reshape(-1,1)))
      
    grad = (1.0/m)*XX.T.dot(h-y) + (reg/m)*np.r_[[[0]],theta[1:].reshape(-1,1)]
        
    return(grad.flatten())

initial_theta = np.zeros(XX.shape[1])
costFunctionReg(initial_theta, 1, XX, y)

fig, axes = plt.subplots(1,3, sharey = True, figsize=(17,5))

# 決策邊界，咱們分別來看看正則化係數lambda太大太小分別會出現什麼情況
# Lambda = 0 : 就是沒有正則化，這樣的話，就過擬合咯
# Lambda = 1 : 這才是正確的開啟方式
# Lambda = 100 : 臥槽，正則化項太激進，導致基本就沒擬合出決策邊界

for i, C in enumerate([0.0, 1.0, 100.0]):
    # 最優化 costFunctionReg
    res2 = minimize(costFunctionReg, initial_theta, args=(C, XX, y), jac=gradientReg, options={'maxiter':3000})
    
    # 準確率
    accuracy = 100.0*sum(predict(res2.x, XX) == y.ravel())/y.size    

    # 對X,y的雜湊繪圖
    plotData(data2, 'Microchip Test 1', 'Microchip Test 2', 'y = 1', 'y = 0', axes.flatten()[i])
    
    # 畫出決策邊界
    x1_min, x1_max = X[:,0].min(), X[:,0].max(),
    x2_min, x2_max = X[:,1].min(), X[:,1].max(),
    xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max), np.linspace(x2_min, x2_max))
    h = sigmoid(poly.fit_transform(np.c_[xx1.ravel(), xx2.ravel()]).dot(res2.x))
    h = h.reshape(xx1.shape)
    axes.flatten()[i].contour(xx1, xx2, h, [0.5], linewidths=1, colors='g');       
    axes.flatten()[i].set_title('Train accuracy {}% with Lambda = {}'.format(np.round(accuracy, decimals=2), C))