高斯金字塔的作用：模擬人類的視覺，近處的東西看著大，並且能夠看到東西的細節所在，當把這東西從眼前拿到幾米外，雖然還是能看到東西，但也只能窺見它的輪廓了，對於細節無從得知。

高斯金字塔就是模擬了這樣的一種視覺特性，當對影象進行下采樣的時候，影象的解析度降低，就好比把東西從近處拿到了遠處。

這裡的向下與向上取樣，是對影象的尺寸而言的（和金字塔的方向相反），向上就是影象尺寸加倍，向下就是影象尺寸減半

通常，影象處理軟體會提供"模糊"（blur）濾鏡，使圖片產生模糊的效果。

"模糊"的演算法有很多種，其中有一種叫做"高斯模糊"（Gaussian Blur）。它將正態分佈（又名"高斯分佈"）用於影象處理。

本文介紹"高斯模糊"的演算法，你會看到這是一個非常簡單易懂的演算法。本質上，它是一種資料平滑技術（data smoothing），適用於多個場合，影象處理恰好提供了一個直觀的應用例項。

一、高斯模糊的原理

所謂"模糊"，可以理解成每一個畫素都取周邊畫素的平均值。

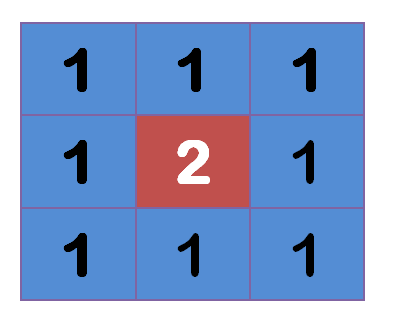
上圖中，2是中間點，周邊點都是1。

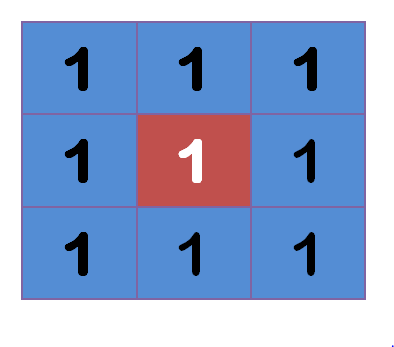
"中間點"取"周圍點"的平均值，就會變成1。在數值上，這是一種"平滑化"。在圖形上，就相當於產生"模糊"效果，"中間點"失去細節。

顯然，計算平均值時，取值範圍越大，"模糊效果"越強烈。

上面分別是原圖、模糊半徑3畫素、模糊半徑10畫素的效果。模糊半徑越大，影象就越模糊。從數值角度看，就是數值越平滑。

接下來的問題就是，既然每個點都要取周邊畫素的平均值，那麼應該如何分配權重呢？

如果使用簡單平均，顯然不是很合理，因為影象都是連續的，越靠近的點關係越密切，越遠離的點關係越疏遠。因此，加權平均更合理，距離越近的點權重越大，距離越遠的點權重越小。

二、正態分佈的權重

正態分佈顯然是一種可取的權重分配模式。

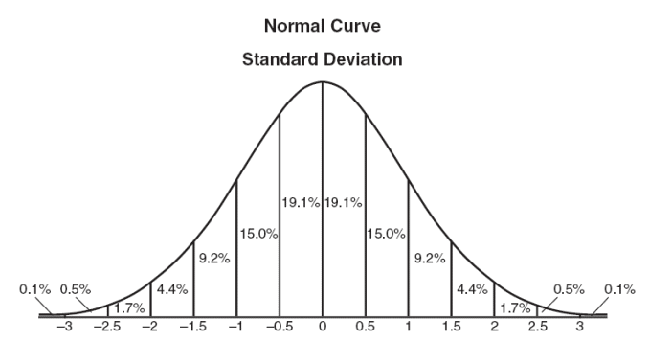
在圖形上，正態分佈是一種鐘形曲線，越接近中心，取值越大，越遠離中心，取值越小。

計算平均值的時候，我們只需要將"中心點"作為原點，其他點按照其在正態曲線上的位置，分配權重，就可以得到一個加權平均值。

三、高斯函式

上面的正態分佈是一維的，影象都是二維的，所以我們需要二維的正態分佈。

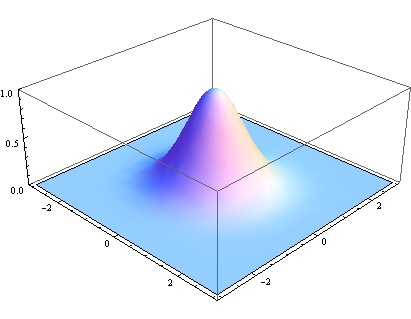
正態分佈的密度函式叫做"高斯函式"（Gaussian function）。它的一維形式是：

其中，μ是x的均值，σ是x的方差。因為計算平均值的時候，中心點就是原點，所以μ等於0。

根據一維高斯函式，可以推導得到二維高斯函式：

有了這個函式 ，就可以計算每個點的權重了。

四、權重矩陣

假定中心點的座標是（0,0），那麼距離它最近的8個點的座標如下：

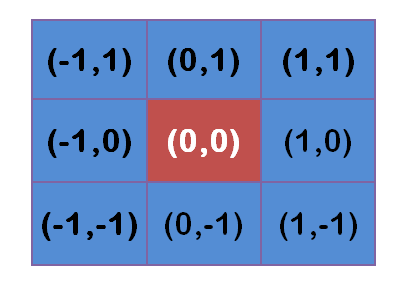
更遠的點以此類推。

為了計算權重矩陣，需要設定σ的值。假定σ=1.5，則模糊半徑為1的權重矩陣如下：

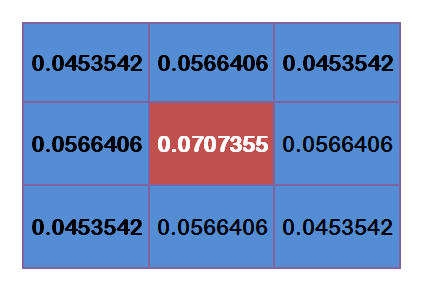
這9個點的權重總和等於0.4787147，如果只計算這9個點的加權平均，還必須讓它們的權重之和等於1，因此上面9個值還要分別除以0.4787147，得到最終的權重矩陣。

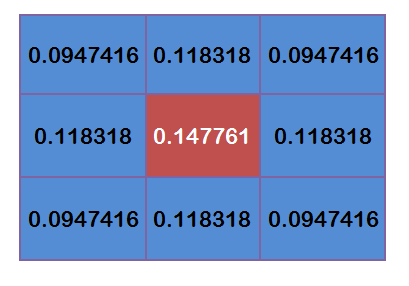
五、計算高斯模糊

有了權重矩陣，就可以計算高斯模糊的值了。

假設現有9個畫素點，灰度值（0-255）如下：

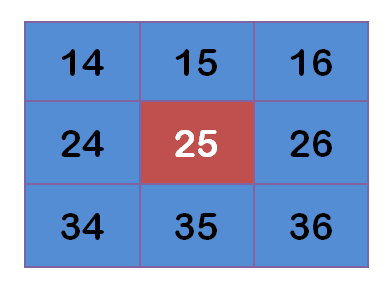
每個點乘以自己的權重值：

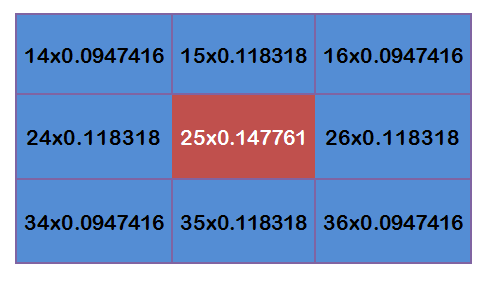
得到

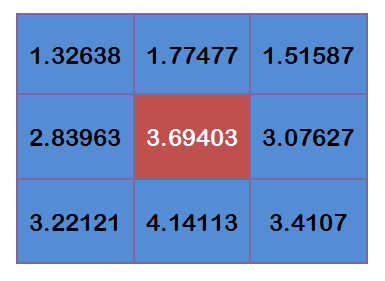
將這9個值加起來，就是中心點的高斯模糊的值。

對所有點重複這個過程，就得到了高斯模糊後的影象。如果原圖是彩色圖片，可以對RGB三個通道分別做高斯模糊。

六、邊界點的處理

如果一個點處於邊界，周邊沒有足夠的點，怎麼辦？

一個變通方法，就是把已有的點拷貝到另一面的對應位置，模擬出完整的矩陣。

尺度空間理論

自然界中的物體隨著觀測尺度不同有不同的表現形態。例如我們形容建築物用“米”，觀測分子、原子等用“納米”。更形象的例子比如Google地圖，滑動滑鼠輪可以改變觀測地圖的尺度，看到的地圖繪製也不同；還有電影中的拉伸鏡頭等等……

尺度空間中各尺度影象的模糊程度逐漸變大，能夠模擬人在距離目標由近到遠時目標在視網膜上的形成過程。
尺度越大影象越模糊。

為什麼要討論尺度空間？

用機器視覺系統分析未知場景時，計算機並不預先知道影象中物體的尺度。我們需要同時考慮影象在多尺度下的描述，獲知感興趣物體的最佳尺度。另外如果不同的尺度下都有同樣的關鍵點，那麼在不同的尺度的輸入影象下就都可以檢測出來關鍵點匹配，也就是尺度不變性。

影象的尺度空間表達就是影象在所有尺度下的描述。

尺度空間表達與金字塔多解析度表達

高斯模糊

二維空間高斯函式：

尺度空間：

尺度是自然客觀存在的，不是主觀創造的。高斯卷積只是表現尺度空間的一種形式。

二維空間高斯函式是等高線從中心成正太分佈的同心圓：

分佈不為零的點組成卷積陣與原始影象做變換，即每個畫素值是周圍相鄰畫素值的高斯平均。一個5*5的高斯模版如下所示：

高斯模版是圓對稱的，且卷積的結果使原始畫素值有最大的權重，距離中心越遠的相鄰畫素值權重也越小。
在實際應用中，在計算高斯函式的離散近似時，在大概3σ距離之外的畫素都可以看作不起作用，這些畫素的計算也就可以忽略。所以，通常程式只計算(6σ+1)*(6σ+1)就可以保證相關畫素影響。

高斯模糊另一個很厲害的性質就是線性可分：使用二維矩陣變換的高斯模糊可以通過在水平和豎直方向各進行一維高斯矩陣變換相加得到。

O(N^2*m*n)次乘法就縮減成了O(N*m*n)+O(N*m*n)次乘法。（N為高斯核大小，m,n為二維影象高和寬）

其實高斯這一部分只需要簡單瞭解就可以了，在OpenCV也只需要一句程式碼：

1. GaussianBlur(dbl, dbl, Size(), sig_diff, sig_diff);  

我這裡詳寫了一下是因為這塊兒對分析演算法效率比較有用，而且高斯模糊的演算法真的很漂亮~

金字塔多解析度

金字塔是早期影象多尺度的表示形式。影象金字塔化一般包括兩個步驟：使用低通濾波器平滑影象；對平滑影象進行降取樣（通常是水平，豎直方向1/2），從而得到一系列尺寸縮小的影象。

上圖中（a）是對原始訊號進行低通濾波，（b）是降取樣得到的訊號。

而對於二維影象，一個傳統的金字塔中，每一層影象由上一層解析度的長、寬各一半，也就是四分之一的畫素組成：

多尺度和多解析度

尺度空間表達和金字塔多解析度表達之間最大的不同是：

• 尺度空間表達是由不同高斯核平滑卷積得到，在所有尺度上有相同的解析度；
• 而金字塔多解析度表達每層解析度減少固定比率。

所以，金字塔多解析度生成較快，且佔用儲存空間少；而多尺度表達隨著尺度引數的增加冗餘資訊也變多。

多尺度表達的優點在於影象的區域性特徵可以用簡單的形式在不同尺度上描述；而金字塔表達沒有理論基礎，難以分析影象區域性特徵。

DoG（Difference of Gaussian）

高斯拉普拉斯LoG金字塔

結合尺度空間表達和金字塔多解析度表達，就是在使用尺度空間時使用金字塔表示，也就是計算機視覺中最有名的拉普拉斯金子塔（《The Laplacian pyramid as a compact image code》）。

高斯拉普拉斯LoG（Laplace of Guassian）運算元就是對高斯函式進行拉普拉斯變換：

核心思想還是高斯，這個不多敘述。

高斯差分DoG金字塔

DoG（Difference of Gaussian）其實是對高斯拉普拉斯LoG的近似，也就是對的近似。SIFT演算法建議，在某一尺度上的特徵檢測可以通過對兩個相鄰高斯尺度空間的影象相減，得到DoG的響應值影象D(x,y,σ)。然後仿照LoG方法，通過對響應值影象D(x,y,σ)進行區域性最大值搜尋，在空間位置和尺度空間定位區域性特徵點。其中：

k為相鄰兩個尺度空間倍數的常數。

上圖中（a）是DoG的三維圖，（b）是DoG與LoG的對比。