(周志華)讀書筆記 -- 第二章 模型評估與選擇
阿新 • • 發佈:2018-12-30
隨手記下所學知識,很多圖表來自原書,僅供學習使用!
2.1 經驗誤差與過擬合
通常,我們使用"錯誤率"來表示分類中錯誤的樣本佔總樣本的比例.如果m個樣本中有a個錯誤樣本則錯誤率E=a/m
,對應的,1-a/m稱為精度,即"精度"=1-"錯誤率".更一般的情況來說,我們把機器學習的預測輸出和樣本真實輸出之間的差異稱為"訓練誤差"或者"經驗誤差".
一般來說,如果在訓練集中的表現精度高,而在測試集中表現的精度小,一般是過擬合.相反,如果是精度都不高一般是欠擬合.我們本來的目的是把訓練集這一類的特徵學出來,也就是要找訓練集和測試集的共同特徵,但是,雖然類有共性,但是每個個體之間是有差異的,如果是把訓練集自身的特徵當成了這一類的特徵,就是過擬合,如果,沒有學到什麼,訓練集(有可能訓練集也不低)測試集精度低,一般就是過擬合.比如說,訓練的時候是用的哈士奇,但是測試的時候是金毛,如果因為金毛耳朵,顏色和哈士奇不一樣而不認為金毛是狗,就是過擬合,但是如果是因為看到體型差不多,就認為是狗,就是欠擬合.(金毛和哈士奇圖片來自網路,侵權就刪...)
更加恰當的例子應該還是來自與原書.
2.2 評估方法
在測試過程中,我們一般會找一個測試集,測試集資料不在訓練中出現.至於為怎麼,很容易理解,就像學生考試一樣,用平時的訓練題作為考試題,這樣就不能考出來舉一反三的能力,可以看為是機械記憶.機器學習,本來就是要做一個能夠舉一反三的模型,要是考記憶能力,還不如直接弄個記事本,然後Ctrl+F直接查詢檔案中的關鍵字.
那麼還有一個問題,資料集就有一個,既要測試,又要訓練應該如何做呢?很簡單,分一為二.直接把一個數據集分成兩個,一個作為資料集,一個作為訓練集.
2.2.1留出法
"留出法"是將資料集分成兩個相斥的集合.但是要保證是均勻的劃分,簡單的說是把資料集打亂以後在裡面抽取多少是個有效的辦法.例如,對於判斷是否是樹葉這個資料中,把是的一類和不是的分開.那麼這個劃分基本上就是沒有意義的.2.2.2 交叉驗證法
其實上面的劃分方法有個問題,就是貌似沒有充分利用每個資料來訓練模型.對於這個問題,人們又想到了一個方法,就是把資料混合均勻以後,分成沒有交集的k份,每一次把其中的一份作為測試,其他作為訓練,然後對k個結果求平均.這個方法成為"K折交叉驗證",一般人們把k取值為10.如果有m的資料而k=m,那麼這個情況就比較特殊了,就被成為了"留一法".留一法能夠保證讓每次的訓練集和原來的資料集儘可能的接近,從而保證了準確性.但是,想想就知道,恐怕要訓練測試m次了,而m很大的時候,幾乎不可能實現(當然,有恆心有毅力者大有人在). 簡單的圖片來說明就是: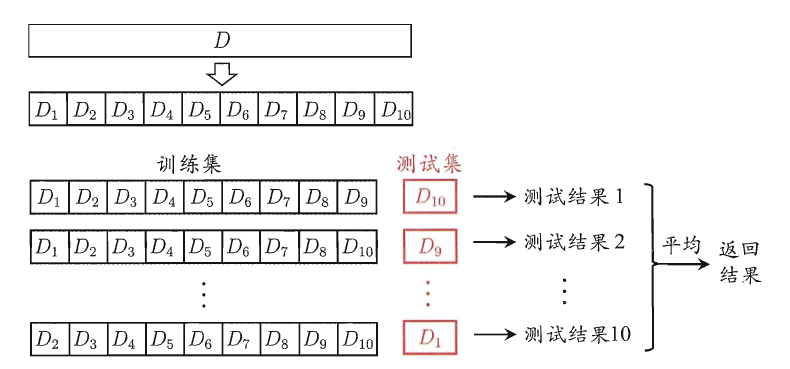
2.2.3 自助法
自助法,就是一個高中概率常見的模型,有放回的摸小球的問題.就是把資料集混合均勻以後,開始有放回的抽取m次,作為訓練集,然後把資料集和訓練集的差集作為測試集.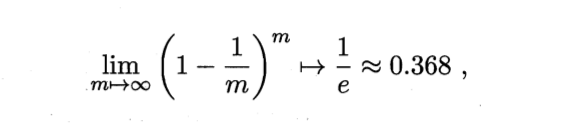 也就是有0.368的資料在測試集.好熟悉的公式,考研數學沒白看...
也就是有0.368的資料在測試集.好熟悉的公式,考研數學沒白看...
2.2.4 調引數與最終模型
有人說,機器學習尤其是神經網路,就是調參。這個我也不知道是不是對的,但是調參是很重要的,據說厲害的人知道每一個引數與結果的關係,不斷調整然後結果自然就好了,而盲目調參,就是碰運氣咯。這個肯定是根據後面的章節的知識進行操作的。2.3 效能度量
效能度量,顧名思義就是考察對比不同演算法的好壞的,衡量模型泛化能力的評價標準,就是效能度量。 懶得寫了,貼點原書的“均方誤差”。 但是還有的效能度量:
但是還有的效能度量:
2.3.1 錯誤率與精度
錯誤率與精度的公式為: 在這裡,我感覺就是巨集觀來看,資料集的平均錯誤率和準確率,就是拿一個數據出來錯誤的概率和正確的概率。
而當加入了一個概率密度,就成了概率的概率了.
在這裡,我感覺就是巨集觀來看,資料集的平均錯誤率和準確率,就是拿一個數據出來錯誤的概率和正確的概率。
而當加入了一個概率密度,就成了概率的概率了.
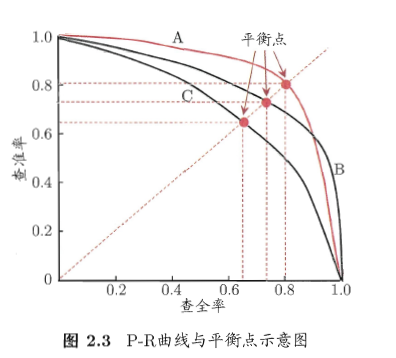
2.3.2 查準率、查全率和F1
首先看看二分問題的結果混餚矩陣來看查準率和查全率:



2.3.3 ROC與AUC
ROC全稱是“受試者工作特徵”。其實就是上面的p-r圖的座標換了換。
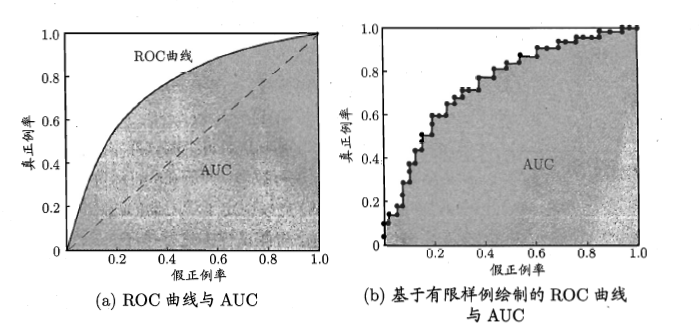 這個判斷標準和P-R圖一樣,看面積。當看到b圖的時候,是不是想起了積分了呢?
這個判斷標準和P-R圖一樣,看面積。當看到b圖的時候,是不是想起了積分了呢?
2.3.4 代價敏感錯誤率與代價曲線
嗯,生活中,有大錯誤也有小錯誤。大錯誤一旦犯了,就麻煩了,小錯誤可能天天犯都沒事啊。所以,這裡引入了代價問題,看看錯誤是致命錯誤還是小毛病。
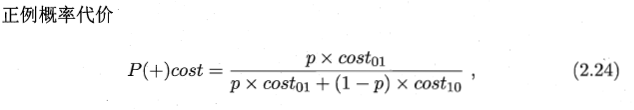
2.4 比較檢驗
2.4.1 假設檢驗
看到這一節開始,我感覺我學的是假計算機,感覺好像進入了數學系。。。 貌似本小結開始前,應該先想想那個排列組合,比如說,有m個小球,不放回的抽取e個小球標記為錯誤,其他的標記為正確,那麼有幾種可能?這樣想一下,原書中的公式似乎就熟悉多了呢。


