在上一節我們已經知道tarjan演算法可以求聯通圖，在這裡我們也運用tarjan的思想求割點與割邊，首先我們先來說說割點，那麼什麼事割點呢，先來看一張圖（a）,圖片來自網路

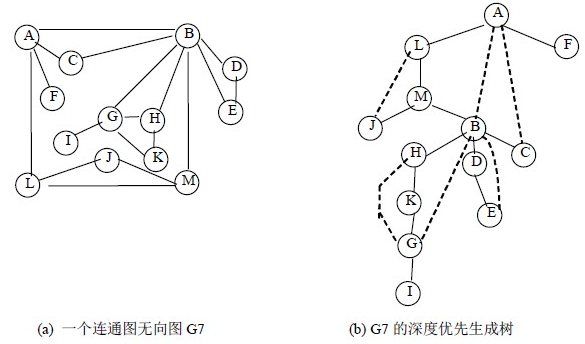
 在（a）圖中，我們將A點以及與A點相連的邊全部去除，會發現這個聯通圖被分成了倆個聯通圖，一個是節點F，另外一個是餘下的所有的節點組成的圖，因此我們將A點稱為割點，同理我們發現B點也是割點，因此我們可以這樣定義割點，在一個無向聯通圖中，如果刪除某個節點後，圖不再連通（即任意倆點之間不能相互到達），我們稱這樣的頂點為割點（定義來自啊哈演算法），那麼問題來了，如何求割點呢？？？

很容易的一個想法就是我們每次刪除一個節點後用bfs或者dfs來遍歷圖是否依然聯通，如果不聯通則該點是割點，這種方法的複雜度是O（N（N + M）），太暴力了，我們來想想其他的方法

再介紹其他方法前，我們再來了解幾個定義（定義來源於網路）

• DFS搜尋樹：用DFS對圖進行遍歷時，按照遍歷次序的不同，我們可以得到一棵DFS搜尋樹，如圖(b)所示。
• 樹邊：（在[2]中稱為父子邊），在搜尋樹中的實線所示，可理解為在DFS過程中訪問未訪問節點時所經過的邊。
• 回邊：（在[2]中稱為返祖邊、後向邊），在搜尋樹中的虛線所示，可理解為在DFS過程中遇到已訪問節點時所經過的邊。

通過觀察圖（2），我們發現有倆類節點可能成為割點

1. 對根節點u，若其有兩棵或兩棵以上的子樹，則該根結點u為割點；（說明刪除該節點會產生至少倆棵不聯通的子樹）
2. 對非葉子節點u（非根節點），若其子樹的節點均沒有指向u的祖先節點的回邊，說明刪除u之後，根結點與u的子樹的節點不再連通；則節點u為割點。（在這裡可以簡單畫個圖理解一下）

對於這倆類節點，前者我們很容易判斷，我們就不做過多的說明了，具體的判斷會在程式碼裡面講解，我們來說說後者的判斷

我們用dfn[u]記錄節點u在DFS過程中被遍歷到的次序號，low[u]記錄節點u或u的子樹通過非父子邊追溯到最早的祖先節點（即DFS次序號最小），那麼low[u]的計算過程如下：

low[u]={min{low[u], low[v]}，（（u，v）為樹邊）

low【u】 = min{low[u], dfn[v]}    (u,v)為回邊且v不為u的父親節點

至於為什麼不為u的父親節點我暫時還沒有想明白......

關於dfn和low陣列的計算請參考我另外一篇部落格或者去百度上查詢資料，這個不好用語言描述，我就暫且大家都知道了

那麼對於第二類節點，當(u,v)為樹邊且low[v] >= dfn[u]時，節點u才為割點。該式子的含義：表示v節點不能繞過u節點從而返回到更早的祖先，因此u節點為割點

下面來看程式碼實現，在程式碼裡面會做詳細的解說

#include<iostream>
#include<cmath>
using namespace std;
int n, m, root, a, b, total;
int e[101][101], dfn[101], low[101], flag[101], head[101];

//鏈式前向星，不懂的自行百度
struct node{
    int to;
    int next;
}edge[10010];

int cnt = 1;

//前向星建圖
void add(int u, int v) {
    edge[cnt].to = v;
    edge[cnt].next = head[u];
    head[u] = cnt++;
}

void tarjan(int u, int father) {
    int child = 0;//child用來記錄在生成樹中當前頂點的兒子的個數
    dfn[u] = low[u] = ++total;//時間戳
    for (int i = head[u]; i != 0; i = edge[i].next) {//前向星遍歷該頂點的所有邊
        int v = edge[i].to;//該頂點連線的頂點
        if (!dfn[v]) {//如果時間戳為0說明沒有訪問過
            child++;
            tarjan(v, u);//繼續往下搜尋
            low[u] = min(low[u], low[v]);//更新當前時間戳
            //  如果當前節點是根節點並且兒子個數大於等於2，則滿足第一類節點，為割點
            if (u == root && child >= 2) {
                flag[u] = 1;
            //不為根結點但是滿足第二類條件的節點
            } else if (u != root && low[v] >= dfn[u]) {
                flag[u] = 1;
            }
            //如果頂點被訪問過並且不是該節點的父親，說明此時的v為u的祖先，因此需要更新最早頂點的時間戳
        } else if (v != father) {
            low[u] = min(low[u], dfn[v]);
        }
    }
}


int main() {
    cin >> n >> m;
    for (int i = 0; i < m; i++) {
        cin >> a >> b;
        add(a, b);
        add(b, a);
    }
    root = 1; //假設1為根節點
//從1號頂點開始進行深度優先搜尋(tarjan)
    tarjan(1, root);
    for (int i = 1; i <= n; i++) {
        if(flag[i]) {
            cout << i << " ";
        }
    }
    return 0;
}

給一組資料拿來測試一下該程式碼

6 7（6個頂點，7條無向邊）

1 4

1 3

4 2

3 2

2 5

2 6

5 6

輸出為 2

如果有多組圖，那麼我們使用另外的一組程式碼，見下

#include<iostream>
using namespace std;
const int maxn = 20010;
const int maxv = 200010;
int cnt = 1, n, m, total, a, b;
int head[maxn], flag[maxn], dfn[maxn], low[maxn], sum;

struct node{
    int to;
    int next;
}edge[maxv];

void add(int u, int v) {
    edge[cnt].to = v;
    edge[cnt].next = head[u];
    head[u] = cnt++;
}

void tarjan(int u, int father) {
    int child = 0;
    dfn[u] = low[u] = ++total;
    for (int i = head[u]; i != 0; i = edge[i].next) {
        int v = edge[i].to;
        if (!dfn[v]) {
            tarjan(v, father);
            low[u] = min(low[u], low[v]);
            if (low[v] >= dfn[u] && u != father) {
                flag[u] = 1;
            }
            if (u == father) child++;
        }
        low[u] = min(low[u], dfn[v]);
    }
    if (child >= 2 && u == father) {
        flag[u] = 1;
    }
}

int main () {
    cin >> n >> m;
    for (int i = 0; i < m; i++) {
        cin >> a >> b;
        add(a, b);
        add(b, a);
    }
    for (int i = 1; i <= n; i++) {
        if (!dfn[i]) {
            tarjan(i, i);
        }
    }
    for (int i = 1; i <= n; i++) {
        if (flag[i]) sum++;
    }
    cout << sum << endl;
    for (int i = 1; i <= n; i++) {
        if (flag[i]) {
            cout << i << " ";
        }
    }
    return 0;
}

瞭解完割點後我們再來了解什麼是割邊，其實很簡單，即在一個無向聯通圖中，如果刪除某條邊後，圖不在聯通，那麼該條邊稱為割邊，程式碼和上面的程式碼基本上一模一樣，只要改一個小地方，就是將low【v】 >= dfn[u] 改為 low【v】> dfs

[u]即可，前者便是還可以回到父親，後者表示連父親都回不到了，倘若頂點v不能回到祖先，也沒有另外一條路可以回到父親，那麼u-v這條邊就是割邊，其實仔細想想模擬個圖就明白了，程式碼實現如下

#include<iostream>
#include<cmath>
using namespace std;
int n, m, root, a, b, total;
int e[101][101], dfn[101], low[101], flag[101], head[101];

struct node{
    int to;
    int next;
}edge[10010];

int cnt = 1;
void add(int u, int v) {
    edge[cnt].to = v;
    edge[cnt].next = head[u];
    head[u] = cnt++;
}

void tarjan(int u, int father) {
    int child = 0;
    dfn[u] = low[u] = ++total;
    for (int i = head[u]; i != 0; i = edge[i].next) {
        int v = edge[i].to;
        if (!dfn[v]) {
            child++;
            tarjan(v, u);
            low[u] = min(low[u], low[v]);
            if  (low[v] > dfn[u]) {
                cout << u << "->" << v << endl;
            }
        } else if (v != father) {
            low[u] = min(low[u], dfn[v]);
        }
    }
}


int main() {
    cin >> n >> m;
    for (int i = 0; i < m; i++) {
        cin >> a >> b;
        add(a, b);
        add(b, a);
    }
    root = 1;
    tarjan(1, root);
    for (int i = 1; i <= n; i++) {
        if(flag[i]) {
            cout << i << " ";
        }
    }
    return 0;
}

如果輸入上面的那組資料那麼不會有輸出，因為沒有割邊，再給出一組資料

6 6

1 4

1 3

4 2

3 2

2 5

5 6

輸出5->6

2->5

割點和割邊就解釋到這裡了，完畢