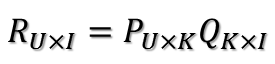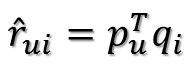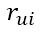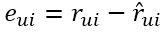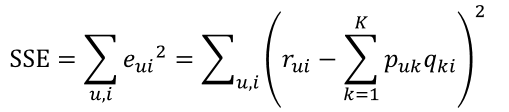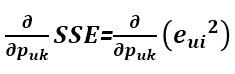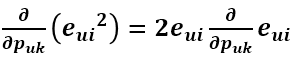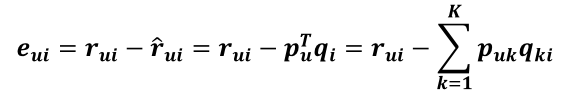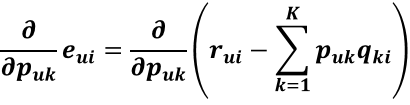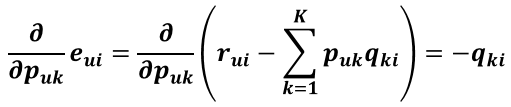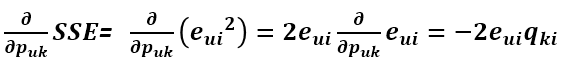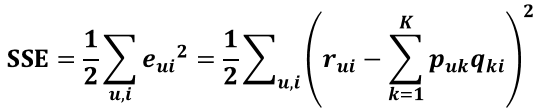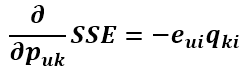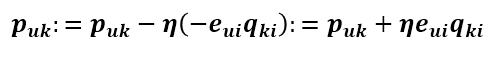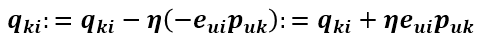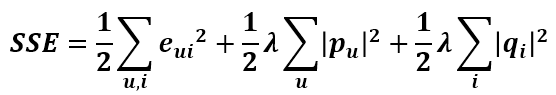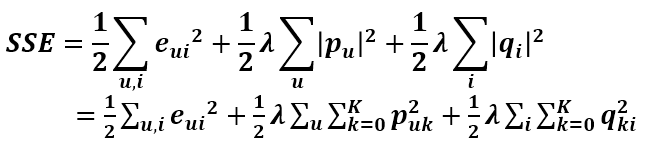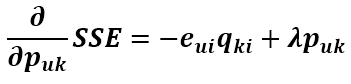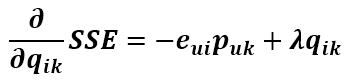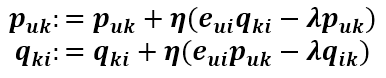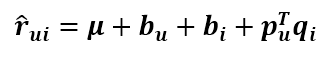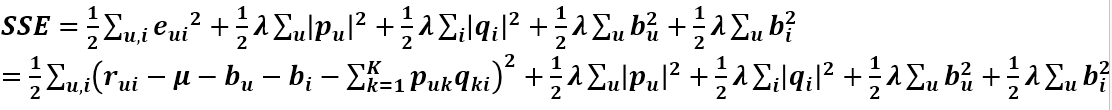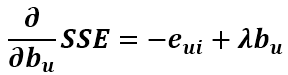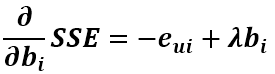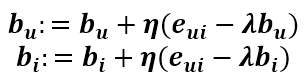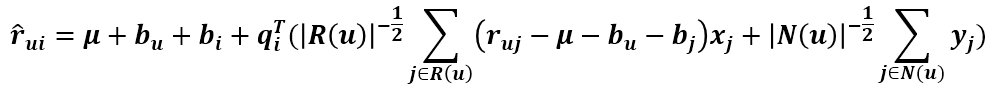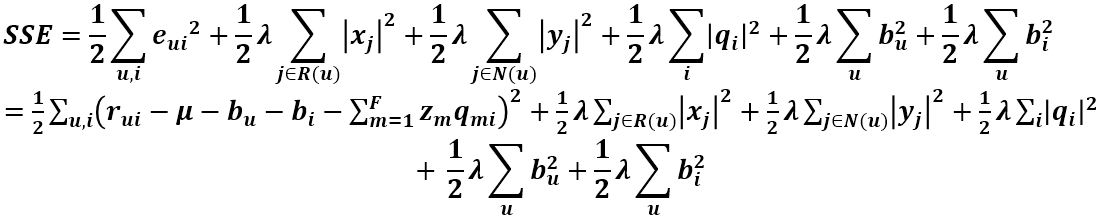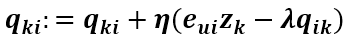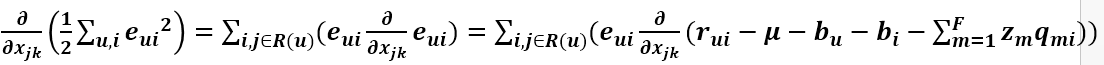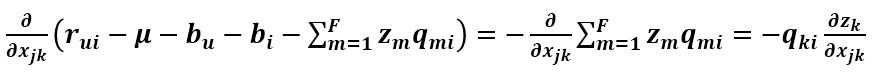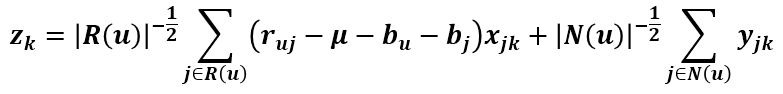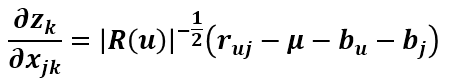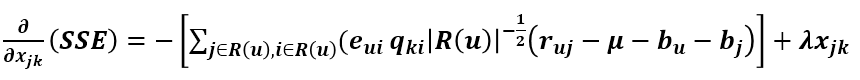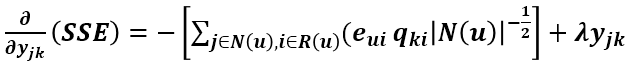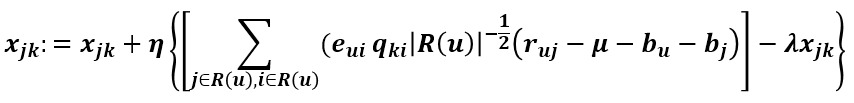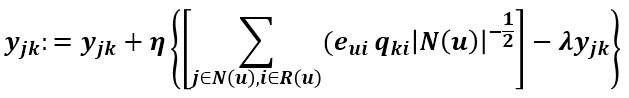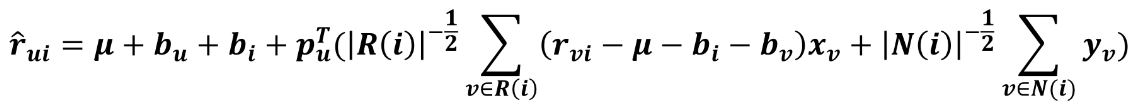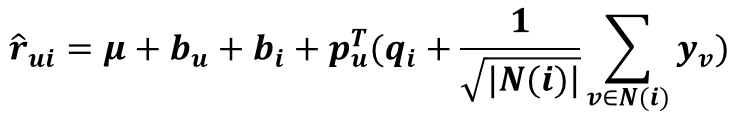推薦演算法學習-SVM,RSVM,ASVM,SVDPP學習公式推導
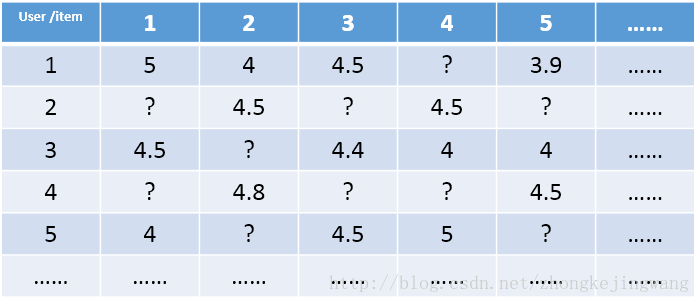
下面開始介紹SVD演算法,假設存在以下user和item的資料矩陣:
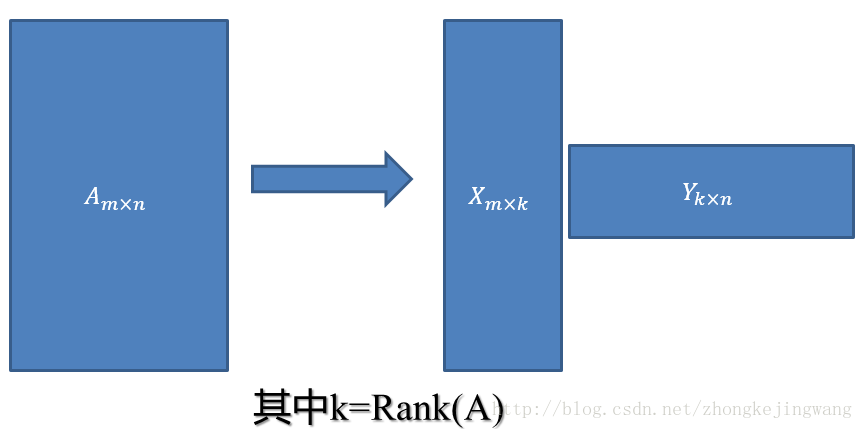
這是一個極其稀疏的矩陣,這裡把這個評分矩陣記為R,其中的元素表示user對item的打分,“?”表示未知的,也就是要你去預測的,現在問題來了:如何去預測未知的評分值呢?上一篇文章用SVD證明了對任意一個矩陣A,都有它的滿秩分解:
那麼剛才的評分矩陣R也存在這樣一個分解,所以可以用兩個矩陣P和Q的乘積來表示評分矩陣R:
上圖中的U表示使用者數,I表示商品數。然後就是利用R中的已知評分訓練P和Q使得P和Q相乘的結果最好地擬合已知的評分,那麼未知的評分也就可以用P的某一行乘上Q的某一列得到了:
這是預測使用者u對商品i的評分,它等於P矩陣的第u行乘上Q矩陣的第i列。這個是最基本的SVD演算法,那麼如何通過已知評分訓練得到P和Q的具體數值呢?
假設已知的評分為:
則真實值與預測值的誤差為:
繼而可以計算出總的誤差平方和:
只要通過訓練把SSE降到最小那麼P、Q就能最好地擬合R了。那又如何使SSE降到最小呢?下面介紹一個常用的區域性優化演算法。
梯度下降法
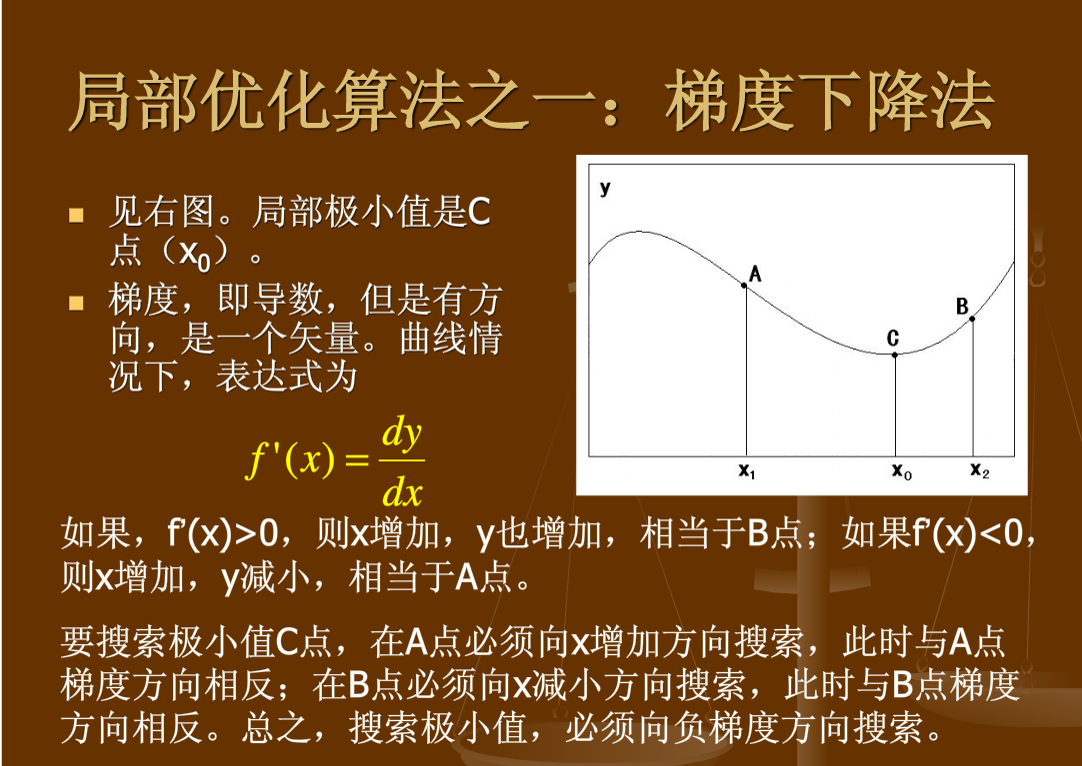
為了說明梯度下降法,我找了一張PPT:
也就是說如果要最小化目標函式,必須往其負梯度方向搜尋。這就是梯度下降法,注意它是一個區域性優化演算法,也就是說有可能落到區域性最優解而不是全域性最優解。
Basic SVD
利用梯度下降法可以求得SSE在Puk變數(也就是P矩陣的第u行第k列的值)處的梯度:
利用求導鏈式法則,e^2先對e求導再乘以e對Puk的求導:
由於
所以
上式中括號裡的那一坨式子如果展開來看的話,其與Puk有關的項只有PukQki,其他的無關項對Puk的求導均等於0
所以求導結果為:
所以
為了讓式子更簡潔,令
這樣做對結果沒有影響,只是為了把求導結果前的2去掉,更好看點。得到
現在得到了目標函式在Puk處的梯度了,那麼按照梯度下降法,將Puk往負梯度方向變化:
令更新的步長(也就是學習速率)為
則Puk的更新式為
同樣的方式可得到Qik的更新式為
得到了更新的式子,現在開始來討論這個更新要怎麼進行。有兩種選擇:1、計算完所有已知評分的預測誤差後再對P、Q進行更新。2、每計算完一個eui後立即對Pu和qi進行更新。這兩種方式都有名稱,分別叫:1、批梯度下降。2、隨機梯度下降。兩者的區別就是批梯度下降在下一輪迭代才能使用本次迭代的更新值,隨機梯度下降本次迭代中當前樣本使用的值可能就是上一個樣本更新的值。由於隨機性可以帶來很多好處,比如有利於避免區域性最優解,所以現在大多傾向於使用隨機梯度下降進行更新。
RSVD
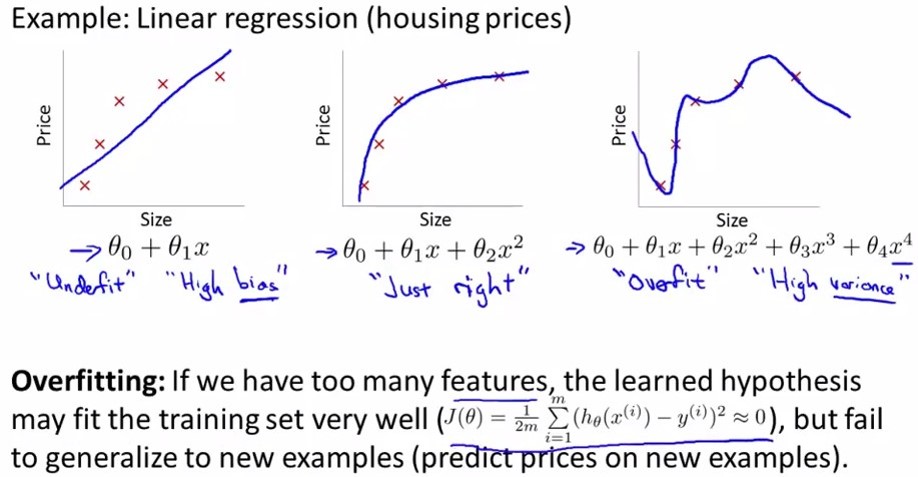
上面就是基本的SVD演算法,但是,問題來了,上面的訓練是針對已知評分資料的,過分地擬合這部分資料有可能導致模型的測試效果很差,在測試集上面表現很糟糕。這就是過擬合問題,關於過擬合與欠擬合可以看一下這張圖
第一個是欠擬合,第二個剛好,第三個過擬合。那麼如何避免過擬合呢?那就是在目標函式中加入正則化引數(加入懲罰項),對於目標函式來說,P矩陣和Q矩陣中的所有值都是變數,這些變數在不知道哪個變數會帶來過擬合的情況下,對所有變數都進行懲罰:
這時候目標函式對Puk的導數就發生變化了,現在就來求加入懲罰項後的導數。
括號裡第一項對Puk的求導前面已經求過了,第二項對Puk的求導很容易求得,第三項與Puk無關,導數為0,所以
同理可得SSE對qik的導數為
將這兩個變數往負梯度方向變化,則更新式為
這就是正則化後的SVD,也叫RSVD。
加入偏置的SVD、RSVD
關於SVD演算法的變種太多了,叫法也不統一,在預測式子上加點引數又會出來一個名稱。由於使用者對商品的打分不僅取決於使用者和商品間的某種關係,還取決於使用者和商品獨有的性質,Koren將SVD的預測公式改成這樣
第一項為總的平均分,bu為使用者u的屬性值,bi為商品i的屬性值,加入的這兩個變數在SSE式子中同樣需要懲罰,那麼SSE就變成了下面這樣:
由上式可以看出SSE對Puk和qik的導數都沒有變化,但此時多了bu和bi變數,同樣要求出其更新式。首先求SSE對bu的導數,只有第一項和第四項和bu有關,第一項對bu的求導和之前的求導類似,用鏈式法則即可求得,第四項直接求導即可,最後可得偏導數為
同理可得對bi的導數為
所以往其負梯度方向變化得到其更新式為
這就是修改後的SVD(RSVD)。
ASVD
全稱叫Asymmetric-SVD,即非對稱SVD,其預測式子為
R(u)表示使用者u評過分的商品集合,N(u)表示使用者u瀏覽過但沒有評過分的商品集合,Xj和Yj是商品的屬性。這個模型很有意思,看預測式子,使用者矩陣P已經被去掉了,取而代之的是利用使用者評過分的商品和使用者瀏覽過尚未評分的商品屬性來表示使用者屬性,這有一定的合理性,因為使用者的行為記錄本身就能反應使用者的喜好。而且,這個模型可以帶來一個很大的好處,一個商場或者網站的使用者數成千上萬甚至過億,儲存使用者屬性的二維矩陣會佔用巨大的儲存空間,而商品數卻沒有那麼多,所以這個模型的好處顯而易見。但是它有個缺點,就是迭代時間太長了,這是可以預見的,以時間換空間嘛。
同樣的,需要計算其各個引數的偏導數,求出更新式,顯然,bu和bi的更新式和剛才求出的一樣
其中的向量z等於下面這坨
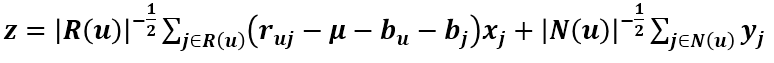
現在要求qik、x和y的更新式,在這裡如果把z看成Pu則根據前面求得的更新式可得qik的更新式:
求Xj的導數需要有點耐心,SSE的第二項對Xj的導數很容易得到,現在來求第一項對Xj的導數:
上式求和符中的i,j都是屬於R(u)的,可以看到Zm只有當m==k時才與Xjk有關,所以
因為
所以
所以得到SSE對Xjk的導數為
同理可得SSE對Yjk的導數為
所以得到Xjk和Yjk的更新方程
這就叫ASVD。。。。。。
SVDPP
最後這個模型也是Koren文章中提到的,SVDPlusPlus(SVD++),它的預測式子為
這裡的N(u)表示使用者u行為記錄(包括瀏覽的和評過分的商品集合)。看了ASVD的更新式推導過程再來看這個應該很簡單,Puk和qik的更新式子不變,Yjk的更新式子和ASVD的更新式一樣:
這些就是Koren在NetFlix大賽中用到的SVD演算法,最後,還有一個需要提的:
對偶演算法
將前面預測公式中的u和i調換位置得到其對偶演算法,對於RSVD而言,u和i的位置是等價的、對稱的,所以其對偶演算法和其本身沒有區別,但對於ASVD和SVD++則不同,有時候對偶演算法得到的結果更加精確,並且,如果將對偶演算法和原始演算法的預測結果融合在一起的話,效果的提升會讓你吃驚!
對偶的ASVD預測公式:
這裡R(i)表示評論過商品i的使用者集合,N(i)表示瀏覽過商品i但沒有評論的使用者集合。由於使用者數量龐大,所以對偶的ASVD會佔用很大空間,這裡需要做取捨了。
對偶的SVD++預測公式:
這裡N(i)表示對商品i有過行為(瀏覽或評分)的使用者集合。
實現這一對偶的操作其實很簡單,只要讀取資料的時候把使用者id和商品id對調位置即可,也就是將R矩陣轉置後再訓練。