\(\color{#0066ff}{題目描述}\)

逆時針給出n個凸多邊形的頂點座標，求它們交的面積。例如n=2時，兩個凸多邊形如下圖：

則相交部分的面積為5.233。

\(\color{#0066ff}{輸入格式}\)

第一行有一個整數n，表示凸多邊形的個數，以下依次描述各個多邊形。第i個多邊形的第一行包含一個整數mi，表示多邊形的邊數，以下mi行每行兩個整數，逆時針給出各個頂點的座標。

\(\color{#0066ff}{輸出格式}\)

輸出檔案僅包含一個實數，表示相交部分的面積，保留三位小數。

\(\color{#0066ff}{輸入樣例}\)

2
6
-2 0
-1 -2
1 -2
2 0
1 2
-1 2
4
0 -3
1 -1
2 2
-1 0
 

\(\color{#0066ff}{輸出樣例}\)

5.233

\(\color{#0066ff}{資料範圍與提示}\)

100%的資料滿足：2<=n<=10，3<=mi<=50，每維座標為[-1000,1000]內的整數

\(\color{#0066ff}{題解}\)

半平面交裸題

開兩個結構體儲存點和線

根據輸入方式，自己定義直線方向，那麼半平面的方向就確定了

程式碼中規定的方向是向量左邊

兩個向量求交(\(AC, BE\))

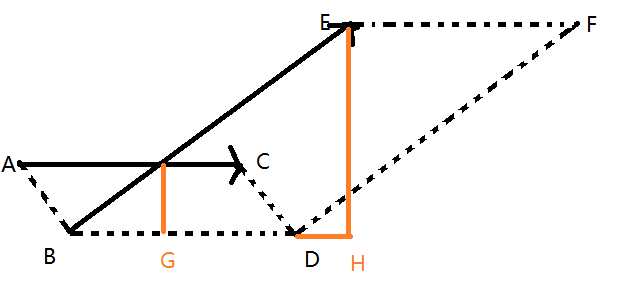
做出這樣的平行四邊形

過E作EH，過p（交點）作PG

顯然BPG，BEH相似，而且作的兩條線為平行四邊形的高

又因為兩個平行四邊形的底相等

所以高之比等於相似比?

通過叉積可以獲得面積比（相似比）

然後\(p = B + k * v_2\)

以上為向量求交點

我們維護一個雙端佇列

每次來一跳新的直線，把收到影響的隊首，隊尾彈出

最後佇列裡就是有效直線

把相鄰的交點都求出來，那麼這個多邊形的面積就是半平面交的面積

#include<bits/stdc++.h>
using namespace std;
#define LL long long
LL in() {
    char ch; int x = 0, f = 1;
    while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
    for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
    return x * f;
}
const int maxn = 505;
double eps = 1e-8;
int T(double x) {
    if(x > eps) return 1;
    if(x < -eps) return -1;
    return 0;
}
struct node {
    double x, y;
    node(double x = 0, double y = 0): x(x), y(y) {}
    node operator + (const node &b) const {
        return node(x + b.x, y + b.y);
    }
    node operator - (const node &b) const {
        return node(x - b.x, y - b.y);
    }
    double operator ^ (const node &b) const {
        return x * b.y - y * b.x;
    }
    double jj() const {
        return atan2(y, x);
    }
    node operator * (double b) const {
        return node(x * b, y * b);
    }
}e[maxn];

struct line {
    node from, to;
    line(node from = node(), node to = node()): from(from), to(to) {}
    double jj() const {
        return (to - from).jj();
    }
    bool operator < (const line &b) const {
        return T(jj() - b.jj()) == 0? T((to - from) ^ (b.to - from)) > 0 : T(jj() - b.jj()) < 0;
    }
}a[maxn], q[maxn];
int n, head, tail, ji;
node to(line i, line j) {
    node x = i.to - i.from, y = j.to - j.from, z = j.from - i.from;
    return j.from + y * ((z ^ x) / (x ^ y)); 
}
bool jud(line x, line y, line z) {
    node p = to(x, y);
    return ((z.to - z.from) ^ (p - z.from)) < 0;
}
void work() {
    std::sort(a + 1, a + ji + 1);
    int cnt = 0;
    for(int i = 1; i <= ji; i++) {
        if(T(a[i].jj() - a[i - 1].jj())) cnt++;
        a[cnt] = a[i];
    }
    head = 1, tail = 0;
    q[++tail] = a[1], q[++tail] = a[2];
    for(int i = 3; i <= cnt; i++) {
        while(head < tail && jud(q[tail - 1], q[tail], a[i])) tail--;
        while(head < tail && jud(q[head + 1], q[head], a[i])) head++;
        q[++tail] = a[i];
    }
    while(head < tail && jud(q[tail - 1], q[tail], q[head])) tail--;
    while(head < tail && jud(q[head + 1], q[head], q[tail])) head++;
    q[tail + 1] = q[head];
    ji = 0;
    for(int i = head; i <= tail; i++) e[++ji] = to(q[i], q[i + 1]);
}

int main() {
    n = in();
    for(int i = 1; i <= n; i++) {
        int F = in();
        for(int j = 1; j <= F; j++) 
            e[j].x = in(), e[j].y = in();
        e[F + 1] = e[1];
        for(int j = 1; j <= F; j++) a[++ji] = line(e[j], e[j + 1]);
    }
    work();
    double ans = 0;
    e[ji + 1] = e[1];
    if(ji > 2) for(int i = 1; i <= ji; i++) ans += (e[i] ^ e[i + 1]);
    printf("%.3f", fabs(ans) / 2.0);
    return 0;
}