二、八、十、十六進位制轉換(圖解篇)
一.本文所涉及的內容(Contents)
二.背景(Contexts)
之前使用SQL把十進位制的整數轉換為三十六進位制,SQL程式碼請參考:SQL Server 進位制轉換函式,其實它是基於二、八、十、十六進位制轉換的計算公式的,進位制之間的轉換是很基礎的知識,但是我發現網路上沒有一篇能把它說的清晰、簡單、易懂的文章,所以我才寫這篇文章的念頭,希望能讓你再也不用擔心、害怕進位制之間的轉換了。
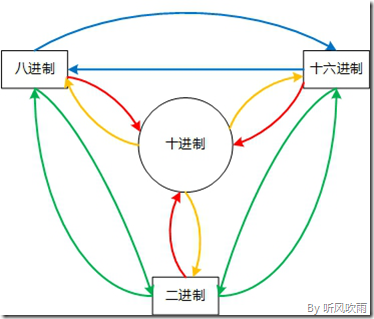
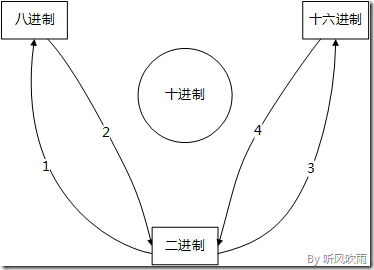
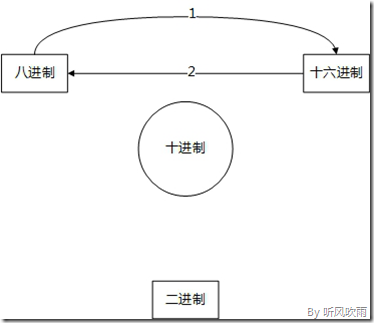
下面是二、八、十、十六進位制之間關係的結構圖:
(Figure1:進位制關係結構圖)
下文會分4個部分對這個圖進行分解,針對每個部分會以圖文的形式進行講解:
- (二、八、十六進位制) → (十進位制);
- (十進位制) → (二、八、十六進位制);
- (二進位制) ↔ (八、十六進位制);
- (八進位制) ↔ (十六進位制);
三.進位制轉換演算法(Convert)
在數字後面加上不同的字母來表示不同的進位制。B(Binary)表示二進位制,O(Octal)表示八進位制,D(Decimal)或不加表示十進位制,H(Hexadecimal)表示十六進位制。例如:(101011)B=(53)O=(43)D=(2B)H
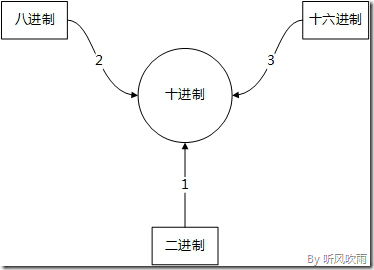
(一) (二、八、十六進位制) → (十進位制)
(Figure2:其他進位制轉換為十進位制)
- 二進位制 → 十進位制
方法:二進位制數從低位到高位(即從右往左)計算,第0位的權值是2的0次方,第1位的權值是2的1次方,第2位的權值是2的2次方,依次遞增下去,把最後的結果相加的值就是十進位制的值了。
例:將二進位制的(101011)B轉換為十進位制的步驟如下:
1. 第0位 1 x 2^0 = 1;
2. 第1位 1 x 2^1 = 2;
3. 第2位 0 x 2^2 = 0;
4. 第3位 1 x 2^3 = 8;
5. 第4位 0 x 2^4 = 0;
6. 第5位 1 x 2^5 = 32;
7. 讀數,把結果值相加,1+2+0+8+0+32=43,即(101011)B=(43)D。
- 八進位制 → 十進位制
方法:八進位制數從低位到高位(即從右往左)計算,第0位的權值是8的0次方,第1位的權值是8的1次方,第2位的權值是8的2次方,依次遞增下去,把最後的結果相加的值就是十進位制的值了。
八進位制就是逢8進1,八進位制數採用 0~7這八數來表達一個數。
例:將八進位制的(53)O轉換為十進位制的步驟如下:
1. 第0位 3 x 8^0 = 3;
2. 第1位 5 x 8^1 = 40;
3. 讀數,把結果值相加,3+40=43,即(53)O=(43)D。
- 十六進位制 → 十進位制
方法:十六進位制數從低位到高位(即從右往左)計算,第0位的權值是16的0次方,第1位的權值是16的1次方,第2位的權值是16的2次方,依次遞增下去,把最後的結果相加的值就是十進位制的值了。
十六進位制就是逢16進1,十六進位制的16個數為0123456789ABCDEF。
例:將十六進位制的(2B)H轉換為十進位制的步驟如下:
1. 第0位 B x 16^0 = 11;
2. 第1位 2 x 16^1 = 32;
3. 讀數,把結果值相加,11+32=43,即(2B)H=(43)D。
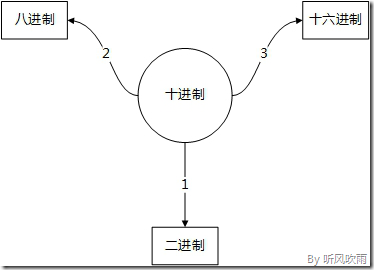
(二) (十進位制) → (二、八、十六進位制)
(Figure3:十進位制轉換為其它進位制)
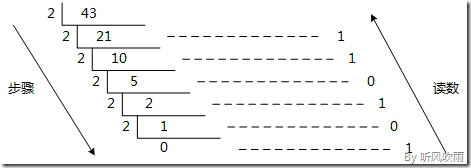
- 十進位制 → 二進位制
方法:除2取餘法,即每次將整數部分除以2,餘數為該位權上的數,而商繼續除以2,餘數又為上一個位權上的數,這個步驟一直持續下去,直到商為0為止,最後讀數時候,從最後一個餘數讀起,一直到最前面的一個餘數。
例:將十進位制的(43)D轉換為二進位制的步驟如下:
1. 將商43除以2,商21餘數為1;
2. 將商21除以2,商10餘數為1;
3. 將商10除以2,商5餘數為0;
4. 將商5除以2,商2餘數為1;
5. 將商2除以2,商1餘數為0;
6. 將商1除以2,商0餘數為1;
7. 讀數,因為最後一位是經過多次除以2才得到的,因此它是最高位,讀數字從最後的餘數向前讀,101011,即(43)D=(101011)B。
(Figure4:圖解十進位制 → 二進位制)
- 十進位制 → 八進位制
方法1:除8取餘法,即每次將整數部分除以8,餘數為該位權上的數,而商繼續除以8,餘數又為上一個位權上的數,這個步驟一直持續下去,直到商為0為止,最後讀數時候,從最後一個餘數起,一直到最前面的一個餘數。
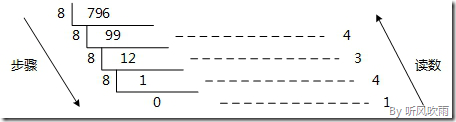
例:將十進位制的(796)D轉換為八進位制的步驟如下:
1. 將商796除以8,商99餘數為4;
2. 將商99除以8,商12餘數為3;
3. 將商12除以8,商1餘數為4;
4. 將商1除以8,商0餘數為1;
5. 讀數,因為最後一位是經過多次除以8才得到的,因此它是最高位,讀數字從最後的餘數向前讀,1434,即(796)D=(1434)O。
(Figure5:圖解十進位制 → 八進位制)
方法2:使用間接法,先將十進位制轉換成二進位制,然後將二進位制又轉換成八進位制;
(Figure6:圖解十進位制 → 八進位制)
- 十進位制 → 十六進位制
方法1:除16取餘法,即每次將整數部分除以16,餘數為該位權上的數,而商繼續除以16,餘數又為上一個位權上的數,這個步驟一直持續下去,直到商為0為止,最後讀數時候,從最後一個餘數起,一直到最前面的一個餘數。
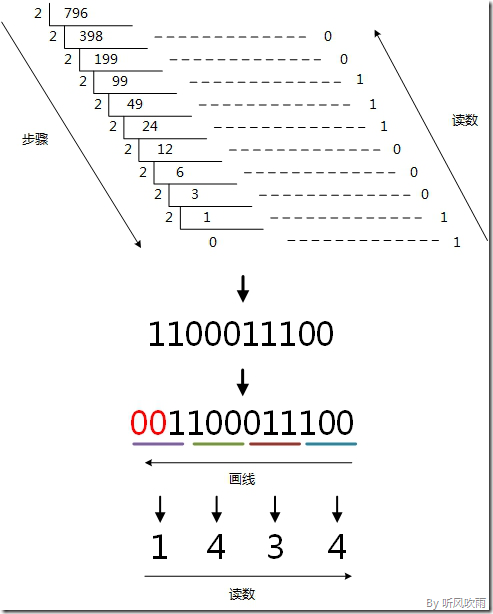
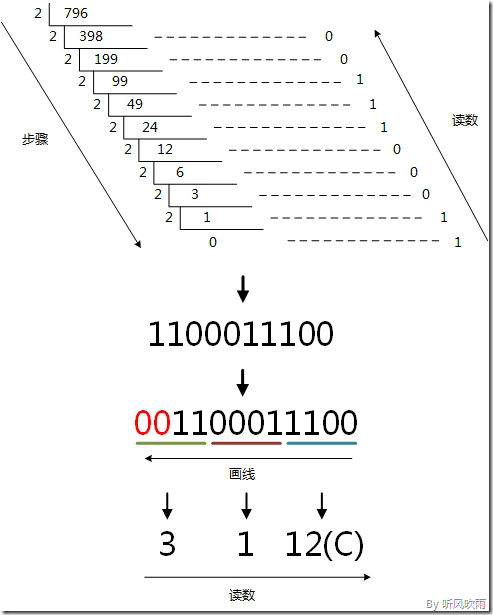
例:將十進位制的(796)D轉換為十六進位制的步驟如下:
1. 將商796除以16,商49餘數為12,對應十六進位制的C;
2. 將商49除以16,商3餘數為1;
3. 將商3除以16,商0餘數為3;
4. 讀數,因為最後一位是經過多次除以16才得到的,因此它是最高位,讀數字從最後的餘數向前讀,31C,即(796)D=(31C)H。
(Figure7:圖解十進位制 → 十六進位制)
方法2:使用間接法,先將十進位制轉換成二進位制,然後將二進位制又轉換成十六進位制;
(Figure8:圖解十進位制 → 十六進位制)
(三) (二進位制) ↔ (八、十六進位制)
(Figure9:二進位制轉換為其它進位制)
- 二進位制 → 八進位制
方法:取三合一法,即從二進位制的小數點為分界點,向左(向右)每三位取成一位,接著將這三位二進位制按權相加,然後,按順序進行排列,小數點的位置不變,得到的數字就是我們所求的八進位制數。如果向左(向右)取三位後,取到最高(最低)位時候,如果無法湊足三位,可以在小數點最左邊(最右邊),即整數的最高位(最低位)添0,湊足三位。
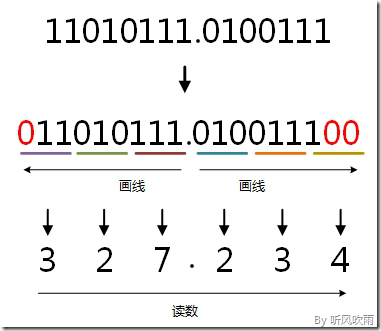
例:將二進位制的(11010111.0100111)B轉換為八進位制的步驟如下:
1. 小數點前111 = 7;
2. 010 = 2;
3. 11補全為011,011 = 3;
4. 小數點後010 = 2;
5. 011 = 3;
6. 1補全為100,100 = 4;
7. 讀數,讀數從高位到低位,即(11010111.0100111)B=(327.234)O。
(Figure10:圖解二進位制 → 八進位制)
二進位制與八進位制編碼對應表:
|
二進位制 |
八進位制 |
|
000 |
0 |
|
001 |
1 |
|
010 |
2 |
|
011 |
3 |
|
100 |
4 |
|
101 |
5 |
|
110 |
6 |
|
111 |
7 |
- 八進位制 → 二進位制
方法:取一分三法,即將一位八進位制數分解成三位二進位制數,用三位二進位制按權相加去湊這位八進位制數,小數點位置照舊。
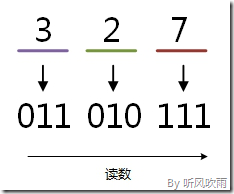
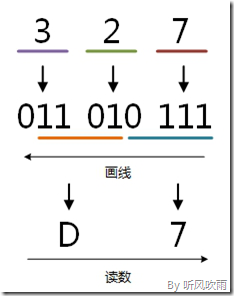
例:將八進位制的(327)O轉換為二進位制的步驟如下:
1. 3 = 011;
2. 2 = 010;
3. 7 = 111;
4. 讀數,讀數從高位到低位,011010111,即(327)O=(11010111)B。
(Figure11:圖解八進位制 → 二進位制)
- 二進位制 → 十六進位制
方法:取四合一法,即從二進位制的小數點為分界點,向左(向右)每四位取成一位,接著將這四位二進位制按權相加,然後,按順序進行排列,小數點的位置不變,得到的數字就是我們所求的十六進位制數。如果向左(向右)取四位後,取到最高(最低)位時候,如果無法湊足四位,可以在小數點最左邊(最右邊),即整數的最高位(最低位)添0,湊足四位。
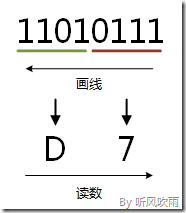
例:將二進位制的(11010111)B轉換為十六進位制的步驟如下:
1. 0111 = 7;
2. 1101 = D;
3. 讀數,讀數從高位到低位,即(11010111)B=(D7)H。
(Figure12:圖解二進位制 → 十六進位制)
- 十六進位制 → 二進位制
方法:取一分四法,即將一位十六進位制數分解成四位二進位制數,用四位二進位制按權相加去湊這位十六進位制數,小數點位置照舊。
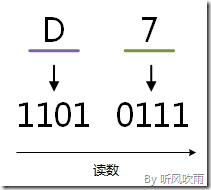
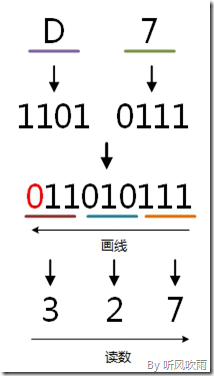
例:將十六進位制的(D7)H轉換為二進位制的步驟如下:
1. D = 1101;
2. 7 = 0111;
3. 讀數,讀數從高位到低位,即(D7)H=(11010111)B。
(Figure13:圖解十六進位制 → 二進位制)
(四) (八進位制) ↔ (十六進位制)
(Figure14:八進位制與十六進位制之間的轉換)
- 八進位制 → 十六進位制
方法:將八進位制轉換為二進位制,然後再將二進位制轉換為十六進位制,小數點位置不變。
例:將八進位制的(327)O轉換為十六進位制的步驟如下:
1. 3 = 011;
2. 2 = 010;
3. 7 = 111;
4. 0111 = 7;
5. 1101 = D;
6. 讀數,讀數從高位到低位,D7,即(327)O=(D7)H。
(Figure15:圖解八進位制 → 十六進位制)
- 十六進位制 → 八進位制
方法:將十六進位制轉換為二進位制,然後再將二進位制轉換為八進位制,小數點位置不變。
例:將十六進位制的(D7)H轉換為八進位制的步驟如下:
1. 7 = 0111;
2. D = 1101;
3. 0111 = 7;
4. 010 = 2;
5. 011 = 3;
6. 讀數,讀數從高位到低位,327,即(D7)H=(327)O。
(Figure16:圖解十六進位制 → 八進位制)
四.擴充套件閱讀
1. 包含小數的進位制換算:
(ABC.8C)H=10x16^2+11x16^1+12x16^0+8x16^-1+12x16^-2
=2560+176+12+0.5+0.046875
=(2748.546875)D
2. 負次冪的計算:
2^-5=2^(0-5)=2^0/2^5=1/2^5
同底數冪相除,底數不變,指數相減,反過來
3. 我們需要了解一個數學關係,即23=8,24=16,而八進位制和十六進位制是用這關係衍生而來的,即用三位二進位制表示一位八進位制,用四位二進位制表示一位十六進位制數。接著,記住4個數字8、4、2、1(23=8、22=4、21=2、20=1)。