使用Python進行層次聚類(三)——層次聚類簇間自然分割方法和評價方法
簇間自然分割方法
今天,主要研究一下層次聚類在進行資料運算的時候,對資料結果進行自然簇分離而需要分析的API————inconsistent()。該函式是計算層次聚類不一致係數的,不一致係數越大,表明使用該閾值進行聚類的偏差越大。這樣按照該不一致係數下的閾值進行聚類即相對於其他情況下的閾值更不適合,因此可以進行自然簇的分離,即取閾值為該不一致係數下小一點即可。解釋在這裡
下面介紹API的使用方法。
首先,我們使用的原始資料如下:(注意,原始資料來源這裡)
origin data : [[2], [8], [0], [4], [1], [9], [9], [0]]
下面為了討論方便,我們把元素資料標籤標號,如:
[2] ==> x[0]
[8] ==> x[1]
…
[0] ==> x[7]
下面使用層次聚類,按照如下方式輸入實驗:
Z = linkage(X, 'single') ==> Z:
analysis:
下面序列從數字8開始,因為原始資料有8個,但是序列從0開始計算,所以使用了0~7號的數字序號。
[[ 2. 7. 0. 2.] <== x[8] = {x[2], x[7]}
[ 5. 6. 0. 2.] <== x[9] = {x[5],x[6]}
[ 0. 4. 1. 2.] <== x[10] = {x[0], x[4]}
[ 8. 10. 1. 4.] <== x[11] = {x[8], x[10]} 顯然,第一列和第二列代表聚集的兩類的序列號,第三列代表第一列和第二列序號所代表的叢集在聚集時的距離(與層次聚類圖的高度相等),第四列代表聚集時所包含的原始資料的個數。
然後為了計算組內均值,按照如下方式輸入實驗:
R = inconsistent(Z) ==> R: (這裡沒有指定d引數,則預設是2,代表進計算到深度為2的資料)
[[ 0. 0. 1. 0. ]
[ 0. 0. 1. 0. ]
[ 1. 0. 1. 0. ]
[ 0.66667 0.57735 3. 0.57735]
[ 0.5 0.70711 2. 0.70711]
[ 1.5 0.70711 2. 0.70711]
[ 2.33333 1.52753 3. 1.09109]]注意,R的行數和Z的行數一樣,計算的時候一一對應。
則:
第一列代表Z對應行聚集時距離的平均值,
第二列代表Z對應行聚集時距離的標準差,
第三列代表計算計算該叢集均值和標準差時選擇的叢集的個數,
第四列代表聚集時的偏值。
下面以上面的例子說明一下。
假設計算R第i行的資料。則按照如下方式計算:
對於第四行的資料:
| Link | Height/Distance |
|---|---|
| x[2] - x[7] | Z[0,2] = 0 |
| x[0] - x[4] | Z[2,2] = 1 |
| x[8] - x[10] | Z[3,2] = 1 |
顯然,對於(1,1,0)組合的平均值對應的R[3,0] = 0.66667, 標準差對應的R[3,1] = 0.57735 (其中標準差計算時是N-1, 不是N)。
偏值計算如下:
在舉一個第七行的資料的例子:
| Link | Height/Distance |
|---|---|
| x[1] - x[9] | Z[4,2] = 1 |
| x[3] - x[11] | Z[5,2] = 2 |
| x[12] - x[13] | Z[6,2] = 4 |
(1,2,4) ==> 平均值 = 2.33333 ==> 標準差 = 1.52753
寫到這裡,也行有人會問了,對於x[11]來說,明明也分為了{x[8], x[10]},為啥計算平均值和標準差的時候不加入進去?
這裡就跟inconsistent()函式傳入的引數K有關了,因為我在使用該函式是,沒有傳入引數K,因此該函式取預設值K=2,這個值代表的是計算平均值時的深度。比如對於第七行資料來說,x[12] - x[13]代表深度1的資料。x[3] - x[11]和x[1] - x[9]代表深度為2的資料。而x[8]-x[10]代表深度為三的資料,預設值是2,所以在計算平均值和標準差時就沒有計算該資料。如果需要計算,則需要改K值即可。如果你想要計算深度到底,則K設定為你輸入資料的長度N即可,因為層次聚類的結果的圖形深度最高也不會超過你資料的長度。
寫到這裡,說一下使用python相關API進行相關資料探勘/機器學習方法的體會: python相關方法確實簡單好用,但是有些說明文件寫的不夠詳細,比如我在看自然簇分類的API的時候根據文件實在是看不懂,最後只好在網上搜各種資料,發現StackOverflow上面有相關介紹,還有就是matlab裡關於層次聚類的介紹,寫的實在是太詳細了,非常棒!強烈建議閱讀。而且相關函式跟python的函式也很像,因此我決定以後用python進行程式設計的時候,遇到文件不清楚的函式,就去查閱matlab相關函式的說明文件,這樣能達到事半功倍的效果。
PS: 別問我為什麼不直接用matlab,python粉不解釋~~
評價方法
關於層次聚類的評價問題。在官方文件中有一個API用來根據計算層次聚類根據結果計算其對應的共表性相關係數(Cophenetic Correlation Coefficient)。共表相關係數越大,表明效果越好。
下面是計算共表相關係數的API
Y = scipy.spatial.distance.pdist((X,'cityblock'); #計算距離列表
Z = hierarchy.linkage(Y,'average'); #進行層次聚類
cluster.hierarchy.cophenet(Z,Y) #計算共表相關係數其中距離矩陣Z的排列方式如下:
比如如下的距離矩陣[1]:
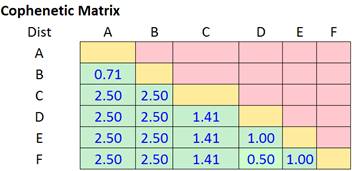
變為如下方式的距離列表,即Y
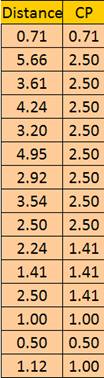
共表相關係數實際上就是計算兩列距離列向量之間的相關係數!
第一列是原始資料之間的距離,第二列是層次聚類之後每個資料之間合併時的距離。
參考:
[1]上述圖和共表相關係數介紹的網址。強烈建議讀這裡介紹的層次聚類的方法的文章,寫的非常詳細具體!)
