今天是元旦放假第一天，想著多睡會，不想改論文了。賴床的時候刷了刷抖音，發現有很多視訊反覆出現這麼一個題目。聲稱是一道農民工出的題目，難倒了幾萬清華北大的高材生。

說實話，這些年來這種UC式的標題讓人很疲勞，標題反正是一個比一個誇張。我仔細看了看題目，分析了一下。題目如下所示。

首先宣告一下我的結論，那就是這個“農民大伯”出的題目不光清華北大的高材生一筆畫不出來，尤拉萊布尼茨掀開棺材板出來也是無能為力。

這個題目實際上就是圖論裡尋找到一條起點到終點的哈密爾頓路徑的問題。哈密爾頓路徑是在1859年，由愛爾蘭數學家哈密爾頓提出的周遊世界遊戲中的一個數學概念。其定義就是在一個圖中，遍歷每個頂點一次且僅一次的路徑稱為哈密爾頓路徑。

我查閱了一下哈密爾頓路徑判定的必要條件，發現似乎都不能應用到這個題目上來。要從數學證明上來解決對我這種圖論已經忘的差不離的菜雞來說還是有點難度。所以我就藉助網上的遍歷窮舉哈密爾頓路徑的方法對於這個問題進行分析，解決。

首先我先將每個格子看成一個頂點，由於圖裡不能有斜線所以我們的問題就是在下面這個圖中求取一條從頂點1到頂點13的哈密爾頓路徑（通過其他所有頂點並且只能通過一次）。

把這個圖用鄰接矩陣表示出來（18個點就是18*18的矩陣，還是有點大噻）

然後用https://blog.csdn.net/zhangyifei521/article/details/53283028

package tiktok;

public class hamilton {

    public static void main(String[] args) {
        hamilton obj = new hamilton();

        int[][] x = {
                {0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
                {1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
                {
 
0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0},
                {0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0},
                {0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0},
                {0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0},
                {1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0},
                {0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0},
                {0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0},
                {0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0},
                {0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0},
                {0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1},
                {0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0},
                {0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0},
                {0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0},
                {0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0},
                {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1},
                {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0}   
        
        };

//        int[][] y = { { 0, 1, 0, 0, 0, 1 }, 
//                      { 1, 0, 1, 0, 0, 1 },
//                      { 0, 1, 0, 1, 1, 0 }, 
//                      { 0, 0, 1, 0, 0, 0 },
//                      { 0, 0, 1, 0, 0, 1 }, 
//                      { 1, 1, 0, 0, 1, 0 } };
//
//        int[][] z = { { 0, 1, 1, 0, 0, 1 }, { 1, 0, 1, 0, 0, 0 },
//                { 1, 1, 0, 1, 0, 1 }, { 0, 0, 1, 0, 1, 0 },
//                { 0, 0, 0, 1, 0, 1 }, { 1, 0, 1, 0, 1, 0 } };

        obj.allHamiltonPath(x); // list all Hamiltonian paths of graph
        // obj.HamiltonPath(z,1); //list all Hamiltonian paths start at point 1

    }

    static int len;
    static int[] path;
    static int count = 0;

    public void allHamiltonPath(int[][] x) { // List all possible Hamilton path
                                                // in the graph
        len = x.length;
        path = new int[len];
        int i;
        for (i = 0; i < len; i++) { // Go through column(of matrix)
            path[0] = i + 1;
            findHamiltonpath(x, 0, i, 0);
        }
    }

//  public void HamiltonPath(int[][] x, int start) { // List all possible
//                                                      // Hamilton path with
//                                                      // fixed starting point
//      len = x.length;
//      path = new int[len];
//      int i;
//      for (i = start - 1; i < start; i++) { // Go through row(with given
//                                              // column)
//          path[0] = i + 1;
//          findHamiltonpath(x, 0, i, 0);
//      }
//  }

    private void findHamiltonpath(int[][] M, int x, int y, int l) {

        int i;
        for (i = x; i < len; i++) { // Go through row

            if (M[i][y] != 0) { // 2 point connect

                if (detect(path, i + 1))// if detect a point that already in the
                                        // path => duplicate
                    continue;

                l++; // Increase path length due to 1 new point is connected
                path[l] = i + 1; // correspond to the array that start at 0,
                                    // graph that start at point 1
                if (l == len - 1) {// Except initial point already count
                                    // =>success connect all point
                    count++;
                    if (count == 1)
                        System.out.println("Hamilton path of graph: ");
                    display(path);
                    l--;
                    continue;
                }

                M[i][y] = M[y][i] = 0; // remove the path that has been get and
                findHamiltonpath(M, 0, i, l); // recursively start to find new
                                                // path at new end point
                l--; // reduce path length due to the failure to find new path
                M[i][y] = M[y][i] = 1; // and tranform back to the inital form
                                        // of adjacent matrix(graph)
            }
        }
        path[l + 1] = 0; // disconnect two point correspond the failure to find
                            // the..
    } // possible hamilton path at new point(ignore newest point try another
        // one)

    public void display(int[] x) {

        System.out.print(count + " : ");
        for (int i : x) {
            System.out.print(i + " ");
        }
        System.out.println();
    }

    private boolean detect(int[] x, int target) { // Detect duplicate point in
                                                    // Halmilton path
        boolean t = false;
        for (int i : x) {
            if (i == target) {
                t = true;
                break;
            }
        }
        return t;
    }
}

執行結果會把所有的哈密爾頓路徑（不限制起點終點）都打印出來，一共有672條哈密爾頓路徑。

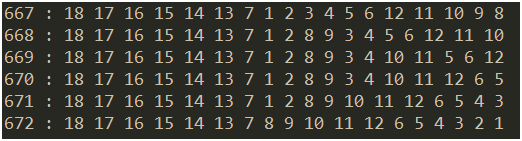
但是如果將起點限制為頂點1，終點限制為頂點13，那麼沒有一條哈密爾頓路徑可以滿足此條件。（起點為1的哈密爾頓路徑有78條，但是沒有一條終點為13）

所以，通過窮舉遍歷的方法，這道農民大伯出的題目是無解的。當然各位抖音上的大神通過摺紙，畫到外面的方式來增加/減少圖中的頂點，也許確實可以找到這樣一條路徑，但是可能也違背了農民大伯的初衷了吧。

另外，如果有大佬知道怎麼數學證明這個問題的話，也歡迎在評論裡留言，大家一起交流學習。