1.2.7&1.2.8 【Deep Learning翻譯系列】Derivatives with a Computation Graph 採用計算圖計算微分
阿新 • • 發佈:2018-12-30
我說神經網路的計算是按正向傳遞或前向傳播步驟組織的,我們計算神經網路的輸出,然後是反向傳遞或反向傳播步驟,我們用於計算梯度或計算導數。計算圖解釋了為什麼它以這種方式組織。我們將通過一個例子說明計算圖(比對數概率迴歸或完整的神經網路更簡單的例子)。
假設我們正在嘗試計算一個函式
,我們令
,
,
,並在計算圖中繪製它們如下。
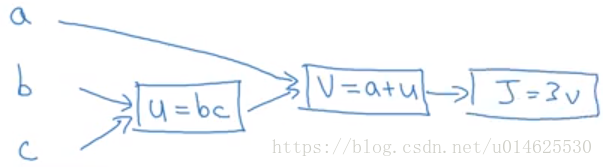
當有一些特殊的輸出變數(例如在這種情況下為
)你想要優化時,計算圖就派上用場了。在對數概率迴歸的情況下,
當然是我們試圖最小化的成本函式。我們在這個小例子中看到的是,通過從左到右的傳遞,你可以計算出
的值。
如果我們將 的數值稍微改變一下, 的值會如何變化?在這裡,我們將 增加了0.001。最終的結果是 增加了0.003。所以 。因為 的增加是 的增加的3倍。
現在讓我們看另一個例子。 ,換句話說,如果我們改變a的值,那麼這對J的值有何影響?
在程式碼中,當你在你編寫的程式碼中計算這個東西時,我們只是使用變數名dvar來表示 。
從這個例子來看,利用計算圖計算導數的關鍵點是,當計算微分時,最有效的方法是按照反向進行從右到左的計算。特別是,我們首先計算 。然後,這對於計算關於 和 是有用的。再往下傳播,這些對於計算關於 和 也是有用的。
