【資料結構與演算法】Huffman樹&&Huffman編碼(附完整原始碼)
出處:http://blog.csdn.net/ns_code/article/details/19174553
Huffman Tree簡介
赫夫曼樹(Huffman Tree),又稱最優二叉樹,是一類帶權路徑長度最短的樹。假設有n個權值{w1,w2,...,wn},如果構造一棵有n個葉子節點的二叉樹,而這n個葉子節點的權值是{w1,w2,...,wn},則所構造出的帶權路徑長度最小的二叉樹就被稱為赫夫曼樹。
這裡補充下樹的帶權路徑長度的概念。樹的帶權路徑長度指樹中所有葉子節點到根節點的路徑長度與該葉子節點權值的乘積之和,如果在一棵二叉樹中共有n個葉子節點,用Wi表示第i個葉子節點的權值,Li表示第i個也葉子節點到根節點的路徑長度,則該二叉樹的帶權路徑長度 WPL=W1*L1 + W2*L2 + ... Wn*Ln。
根據節點的個數以及權值的不同,赫夫曼樹的形狀也各不相同,赫夫曼樹具有如下特性:
- 對於同一組權值,所能得到的赫夫曼樹不一定是唯一的。
- 赫夫曼樹的左右子樹可以互換,因為這並不影響樹的帶權路徑長度。
- 帶權值的節點都是葉子節點,不帶權值的節點都是某棵子二叉樹的根節點。
- 權值越大的節點越靠近赫夫曼樹的根節點,權值越小的節點越遠離赫夫曼樹的根節點。
- 赫夫曼樹中只有葉子節點和度為2的節點,沒有度為1的節點。
- 一棵有n個葉子節點的赫夫曼樹共有2n-1個節點。
Huffman Tree的構建
赫夫曼樹的構建步驟如下:
1、將給定的n個權值看做n棵只有根節點(無左右孩子)的二叉樹,組成一個集合HT,每棵樹的權值為該節點的權值。
2、從集合HT中選出2棵權值最小的二叉樹,組成一棵新的二叉樹,其權值為這2棵二叉樹的權值之和。
3、將步驟2中選出的2棵二叉樹從集合HT中刪去,同時將步驟2中新得到的二叉樹加入到集合HT中。
4、重複步驟2和步驟3,直到集合HT中只含一棵樹,這棵樹便是赫夫曼樹。假如給定如下5個權值:

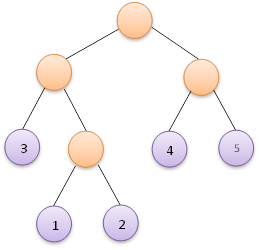
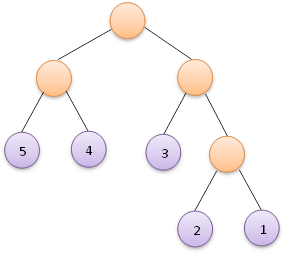
則按照以上步驟,可以構造出如下面左圖所示的赫夫曼樹,當然也可能構造出如下面右圖所示的赫夫曼樹,這並不是唯一的。
Huffman編碼
赫夫曼樹的應用十分廣泛,比如眾所周知的在通訊電文中的應用。在等傳送電文時,我們希望電文的總長儘可能短,因此可以對每個字元設計長度不等的編碼,讓電文中出現較多的字符采用盡可能短的編碼。為了保證在譯碼時不出現歧義,我們可以採取如下圖所示的編碼方式: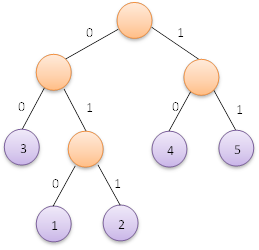
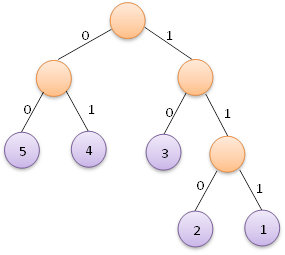
即左分支編碼為字元0,右分支編碼為字元1,將從根節點到葉子節點的路徑上分支字元組成的字串作為葉子節點字元的編碼,這便是赫夫曼編碼。我們根據上面左圖可以得到各葉子節點的赫夫曼編碼如下:
權值為5的也自己節點的赫夫曼編碼為:11 權值為4的也自己節點的赫夫曼編碼為:10 權值為3的也自己節點的赫夫曼編碼為:00 權值為2的也自己節點的赫夫曼編碼為:011 權值為1的也自己節點的赫夫曼編碼為:010
而對於上面右圖,則可以得到各葉子節點的赫夫曼編碼如下: 權值為5的也自己節點的赫夫曼編碼為:00 權值為4的也自己節點的赫夫曼編碼為:01 權值為3的也自己節點的赫夫曼編碼為:10 權值為2的也自己節點的赫夫曼編碼為:110 權值為1的也自己節點的赫夫曼編碼為:111
Huffman編碼的C實現
由於赫夫曼樹中沒有度為1的節點,則一棵具有n個葉子節點的的赫夫曼樹共有2n-1個節點(最後一條特性),因此可以將這些節點儲存在大小為2n-1的一維陣列中。我們可以用以下資料結構來表示赫夫曼樹和赫夫曼編碼: [cpp] view plain copy- /*
- 赫夫曼樹的儲存結構,它也是一種二叉樹結構,
- 這種儲存結構既適合表示樹,也適合表示森林。
- */
- typedef struct Node
- {
- int weight; //權值
- int parent; //父節點的序號,為-1的是根節點
- int lchild,rchild; //左右孩子節點的序號,為-1的是葉子節點
- }HTNode,*HuffmanTree; //用來儲存赫夫曼樹中的所有節點
- typedef char **HuffmanCode; //用來儲存每個葉子節點的赫夫曼編碼
- /*
- 根據給定的n個權值構造一棵赫夫曼樹,wet中存放n個權值
- */
- HuffmanTree create_HuffmanTree(int *wet,int n)
- {
- //一棵有n個葉子節點的赫夫曼樹共有2n-1個節點
- int total = 2*n-1;
- HuffmanTree HT = (HuffmanTree)malloc(total*sizeof(HTNode));
- if(!HT)
- {
- printf("HuffmanTree malloc faild!");
- exit(-1);
- }
- int i;
- //以下初始化序號全部用-1表示,
- //這樣在編碼函式中進行迴圈判斷parent或lchild或rchild的序號時,
- //不會與HT陣列中的任何一個下標混淆
- //HT[0],HT[1]...HT[n-1]中存放需要編碼的n個葉子節點
- for(i=0;i<n;i++)
- {
- HT[i].parent = -1;
- HT[i].lchild = -1;
- HT[i].rchild = -1;
- HT[i].weight = *wet;
- wet++;
- }
- //HT[n],HT[n+1]...HT[2n-2]中存放的是中間構造出的每棵二叉樹的根節點
- for(;i<total;i++)
- {
- HT[i].parent = -1;
- HT[i].lchild = -1;
- HT[i].rchild = -1;
- HT[i].weight = 0;
- }
- int min1,min2; //用來儲存每一輪選出的兩個weight最小且parent為0的節點
- //每一輪比較後選擇出min1和min2構成一課二叉樹,最後構成一棵赫夫曼樹
- for(i=n;i<total;i++)
- {
- select_minium(HT,i,min1,min2);
- HT[min1].parent = i;
- HT[min2].parent = i;
- //這裡左孩子和右孩子可以反過來,構成的也是一棵赫夫曼樹,只是所得的編碼不同
- HT[i].lchild = min1;
- HT[i].rchild = min2;
- HT[i].weight =HT[min1].weight + HT[min2].weight;
- }
- return HT;
- }
- /*
- 從HT陣列的前k個元素中選出weight最小且parent為-1的兩個,分別將其序號儲存在min1和min2中
- */
- void select_minium(HuffmanTree HT,int k,int &min1,int &min2)
- {
- min1 = min(HT,k);
- min2 = min(HT,k);
- }
- /*
- 從HT陣列的前k個元素中選出weight最小且parent為-1的元素,並將該元素的序號返回
- */
- int min(HuffmanTree HT,int k)
- {
- int i = 0;
- int min; //用來存放weight最小且parent為-1的元素的序號
- int min_weight; //用來存放weight最小且parent為-1的元素的weight值
- //先將第一個parent為-1的元素的weight值賦給min_weight,留作以後比較用。
-
相關推薦
【資料結構與演算法】之樹的基本概念及常用操作的Java實現(二叉樹為例) --- 第十二篇
樹是一種非線性資料結構,這種資料結構要比線性資料結構複雜的多,因此分為三篇部落格進行講解: 第一篇:樹的基本概念及常用操作的Java實現(二叉樹為例) 第二篇:二叉查詢樹 第三篇:紅黑樹 本文目錄: 1、基本概念 1.1 什麼是樹 1.2 樹的
【資料結構與演算法】002—樹與二叉樹(Python)
概念 樹 樹是一類重要的非線性資料結構,是以分支關係定義的層次結構 定義: 樹(tree)是n(n>0)個結點的有限集T,其中: 有且僅有一個特定的結點,稱為樹的根(root) 當n>1時,其餘結點可分為m(m>0)個互不相交的有限集T1,T2,……Tm,其中每一個集合本身又是一棵
【資料結構與演算法】字典樹(附完整原始碼)
字典樹簡介 字典書(Trie Tree),又稱單詞查詢樹,是鍵樹的一種,典型應用是用於統計,排序和儲存大量的字串(但不僅限於字串),所以經常被搜尋引擎系統用於文字詞頻統計。 字典樹有3個基本
【資料結構與演算法】Huffman樹&&Huffman編碼(附完整原始碼)
出處:http://blog.csdn.net/ns_code/article/details/19174553 Huffman Tree簡介 赫夫曼樹(Huffman Tree),又稱最優二叉樹,是一類帶權路徑長度最短的樹。假設有n個權值{w1,
【資料結構與演算法】之紅黑樹 --- 第十四篇
樹是一種非線性資料結構,這種資料結構要比線性資料結構複雜的多,因此分為三篇部落格進行講解: 第一篇:樹的基本概念及常用操作的Java實現(二叉樹為例) 第二篇:二叉查詢樹 第三篇:紅黑樹 第三篇:紅黑樹 開篇說明:對於紅黑樹的學習,近階段只需要掌握這種資料結構的思想、特點、適
【資料結構與演算法】之二叉查詢樹 --- 第十三篇
樹是一種非線性資料結構,這種資料結構要比線性資料結構複雜的多,因此分為三篇部落格進行講解: 第一篇:樹的基本概念及常用操作的Java實現(二叉樹為例) 第二篇:二叉查詢樹 第三篇:紅黑樹 本文目錄 1、二叉查詢樹的基本概念 2、二叉查詢樹的查詢操作 3、二叉查詢樹的插
【資料結構與演算法】Size Balanced Tree(SBT)平衡二叉樹
Size Balanced Tree(SBT)平衡二叉樹 定義資料結構 struct SBT { int key,left,right,size; } tree[N]; key:儲存值,left,right:左右子樹,size:保持平衡最終要的資料,表示子
【資料結構與演算法】B/B+ 樹 、RB樹
B / B+ / B*樹採用 多叉樹 結構降低樹深度,主要用在磁碟檔案系統與資料庫。 參考自: B 樹 通常我們所說的 B樹 或 B-樹,其實指的是一種樹,這裡我將其稱為 B樹。 一顆 M
【資料結構與演算法】 利用哈夫曼樹進行檔案壓縮 (部分借鑑網上內容)
哈夫曼編碼(Huffman Coding),又稱霍夫曼編碼,是一種編碼方式,哈夫曼編碼是可變字長編碼(VLC)的一種。Huffman於1952年提出一種編碼方法,該方法完全依據字元出現概率來構造異字頭的平均長度最短的碼字,有時稱之為最佳編碼,一般就叫做Huffman編碼(
【資料結構與演算法】 哈夫曼樹——哈夫曼編碼的一個例項
哈夫曼樹─即最優二叉樹,帶權路徑長度最小的二叉樹,經常應用於資料壓縮。 在計算機資訊處理中,“哈夫曼編碼”是一種一致性編碼法(又稱“熵編碼法”),用於資料的無損耗壓縮。這一術語是指使用一張特殊的編碼表將源字元(例如某檔案中的一個符號)進行編碼。這張編碼表的特殊之處在於,它是根據每一個源字元出現的估算概率而
【資料結構與演算法】紅黑樹常被問到的問題
1.stl中的set底層用的什麼資料結構? 2.紅黑樹的資料結構怎麼定義的? 3.紅黑樹有哪些性質? 4.紅黑樹的各種操作的時間複雜度是多少? 5.紅黑樹相比於BST和AVL樹有什麼優點? 6.紅黑樹相對於雜湊表,在選擇使用的時候有什麼依據? 7.如何擴充套件
【資料結構與演算法】二叉樹遞迴與非遞迴遍歷(附完整原始碼)
二叉樹是一種非常重要的資料結構,很多其他資料機構都是基於二叉樹的基礎演變過來的。二叉樹有前、中、後三種遍歷方式,因為樹的本身就是用遞迴定義的,因此採用遞迴的方法實現三種遍歷,不僅程式碼簡潔且容易理解,但其開銷也比較大,而若採用非遞迴方法實現三種遍歷,則要用棧來模擬實現(遞迴也
【資料結構與演算法】插入排序
插入排序是演算法中的基礎入門和氣泡排序、選擇排序都是必要掌握的。他們都是對比排序,需要通過比較大小交換位置,進行排序。 插入排序的實現思路: 1、 從第一個元素開始,這個元素可以認為已經被排序。 2、取出下一個元素,在已排序的序列中從後往前掃描。 3、如果該元素小於小於前
【資料結構與演算法】 ---快速排序
快速排序流程: 1.從數列中挑出一個基準值 2.將所有比基準值小的擺放在基準前面,所有比基準值大的擺在後面(相同的數可以放到任一邊);在這個分割槽退出之後,該基準就處於數列的中間位置。 3.遞迴地把“基準值前面的子數列”和“基準值後面的子數列”進行排序。 下面以數列
【資料結構與演算法】------氣泡排序
學習開發一年的時間裡,很少去了解排序演算法,氣泡排序也是最開始學習的樣子,靠死記硬背,沒有引入自己的理解。 對於什麼時間複雜度和空間複雜度和穩定性也不清楚其原委,或許在程式碼方面少了幾許的天分: 氣泡排序: 氣泡排序每一輪的比較都是前面的數和後面的數進行比較,並交
【資料結構與演算法】回溯法解決裝載問題
回溯法解決裝載問題(約束函式優化) 解題思想 遍歷各元素,若cw+w[t]<=c(即船可以裝下),則進入左子樹,w[t]標記為1,再進行遞迴,若cw+r>bestw(即當前節點的右子樹包含最優解的可能),則進入右子樹,否則,則不遍歷右子樹。 完整程式碼實現如下 p
【資料結構與演算法】回溯法解決N皇后問題,java程式碼實現
N皇后問題 問題描述 在8×8格的國際象棋上擺放八個皇后,使其不能互相攻擊,即任意兩個皇后都不能處於同一行、同一列或同一斜線上,問有多少種擺法,這稱為八皇后問題。 延伸一下,便為N皇后問題。 核心思想 解決N皇后問題有兩個關鍵點。一是如何進行放置棋子,二是如何驗證棋子是否符合
【資料結構與演算法】貪心演算法解決揹包問題。java程式碼實現
揹包問題(貪心演算法) 貪心演算法思想 簡單的說,就是將大問題轉化為最優子問題,例如本題所要求的,揹包容量有限,要想使物品的總價值最高,那麼,我們必須儘可能的選擇權重高的(即單位價值更高)的物品進行裝載。 在揹包問題中,物品是可拆的,即可以分成任意部分進行裝載,而最終實現的目標是
【資料結構與演算法】連結串列——遞增排序
今天看書時偶然想到的問題,書上是要求將一個數據插入一個有序連結的線性連結串列中, 所以我想先進行連結串列內的資料排序在進行插入資料。 在這裡我只寫了排序的函式。 函式實現: void Sort(LinkList&list, int &n) { f
【資料結構與演算法】線性表——刪除重複元素
線性表是一種隨機存取的結構,和連結串列不同,連結串列順序存取的結構。但是,線性表是一種順序儲存的結構,而連結串列是鏈式儲存結構。兩者都是線性的,但區別不同。 進入主題: 1.假如有一串資料元素,要求刪除其中的重複元素。 首先想到的是用兩層迴圈,第一層從第一個元素開始,第
