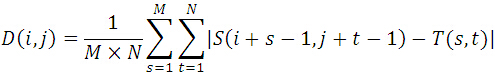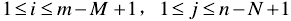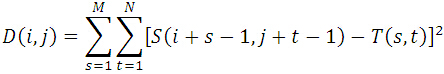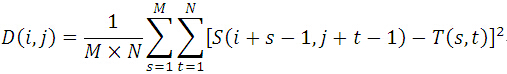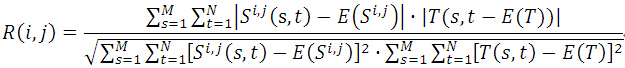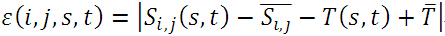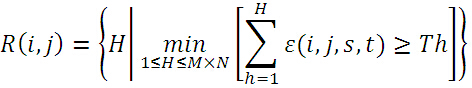為了以後查詢方便，就先存下來吧！（原文：http://blog.csdn.net/hujingshuang/article/details/47759579）

簡介：

       本文主要介紹幾種基於灰度的影象匹配演算法：平均絕對差演算法（MAD）、絕對誤差和演算法（SAD）、誤差平方和演算法（SSD）、平均誤差平方和演算法（MSD）、歸一化積相關演算法（NCC）、序貫相似性檢測演算法（SSDA）、hadamard變換演算法（SATD）。下面依次對其進行講解。

MAD演算法

介紹：平均絕對差演算法（Mean Absolute Differences，簡稱MAD演算法），它是Leese在1971

設S(x,y)是大小為mxn的搜尋影象，T(x,y)是MxN的模板影象，分別如下圖(a)、(b)所示，我們的目的是：在(a)中找到與(b)匹配的區域（黃框所示）。

演算法思路

        在搜尋圖S中，以(i,j)為左上角，取MxN大小的子圖，計算其與模板的相似度；遍歷整個搜尋圖，在所有能夠取到的子圖中，找到與模板圖最相似的子圖作為最終匹配結果。

        MAD演算法的相似性測度公式如下。顯然，平均絕對差D(i,j)越小，表明越相似，故只需找到最小的D(i,j)即可確定能匹配的子圖位置：

其中：

演算法評價：

優點：

①思路簡單，容易理解（子圖與模板圖對應位置上，灰度值之差的絕對值總和，再求平均，實質：是計算的是子圖與模板圖的L1距離的平均值）。

②運算過程簡單，匹配精度高。

缺點：

①運算量偏大。

②對噪聲非常敏感。

——————————————————————————————————————————————————————————————————————————————

SAD演算法

介紹

        絕對誤差和演算法（Sum of Absolute Differences，簡稱SAD演算法）。實際上，SAD演算法與MAD演算法思想幾乎是完全一致，只是其相似度測量公式有一點改動（計算的是子圖與模板圖的L1

演算法實現

由於文章所介紹的幾個演算法非常相似，所以本文僅列出SAD演算法的程式碼，其餘演算法的實現類似。看別人程式碼都相對費力，想自己敲也很簡單。

MATLAB程式碼

1. %%  
2. %絕對誤差和演算法（SAD）  
3. clear all;  
4. close all;  
5. %%  
6. src=imread('lena.jpg');  
7. [a b d]=size(src);  
8. if d==3  
9.     src=rgb2gray(src);  
10. end  
11. mask=imread('lena_mask.jpg');  
12. [m n d]=size(mask);  
13. if d==3  
14.     mask=rgb2gray(mask);  
15. end  
16. %%  
17. N=n;%模板尺寸，預設模板為正方形  
18. M=a;%代搜尋影象尺寸，預設搜尋影象為正方形  
19. %%  
20. dst=zeros(M-N,M-N);  
21. for i=1:M-N         %子圖選取，每次滑動一個畫素  
22.     for j=1:M-N  
23.         temp=src(i:i+N-1,j:j+N-1);%當前子圖  
24.         dst(i,j)=dst(i,j)+sum(sum(abs(temp-mask)));  
25.     end  
26. end  
27. abs_min=min(min(dst));  
28. [x,y]=find(dst==abs_min);  
29. figure;  
30. imshow(mask);title('模板');  
31. figure;  
32. imshow(src);  
33. hold on;  
34. rectangle('position',[y,x,N-1,N-1],'edgecolor','r');  
35. hold off;title('搜尋圖');  

輸出結果

——————————————————————————————————————————————————————————————————————————————

SSD演算法

        誤差平方和演算法（Sum of Squared Differences，簡稱SSD演算法），也叫差方和演算法。實際上，SSD演算法與SAD演算法如出一轍，只是其相似度測量公式有一點改動（計算的是子圖與模板圖的L2距離）。這裡不再贅述。

——————————————————————————————————————————————————————————————————————————————

MSD演算法

        平均誤差平方和演算法（Mean Square Differences，簡稱MSD演算法），也稱均方差演算法。實際上，MSD之餘SSD，等同於MAD之餘SAD（計算的是子圖與模板圖的L2距離的平均值），故此處不再贅述。

————————————————————————————————————————————————————————————————————————————————

NCC演算法

        歸一化積相關演算法（Normalized Cross Correlation，簡稱NCC演算法），與上面演算法相似，依然是利用子圖與模板圖的灰度，通過歸一化的相關性度量公式來計算二者之間的匹配程度。

其中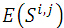，、分別表示(i,j)處子圖、模板的平均灰度值。

————————————————————————————————————————————————————————————————————————

SSDA演算法

        序貫相似性檢測演算法（Sequential Similiarity Detection Algorithm，簡稱SSDA演算法），它是由Barnea和Sliverman於1972年，在文章《A class of algorithms for fast digital image registration》中提出的一種匹配演算法，是對傳統模板匹配演算法的改進，比MAD演算法快幾十到幾百倍。

與上述演算法假設相同：S(x,y)是mxn的搜尋圖，T(x,y)是MxN的模板圖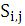，是搜尋圖中的一個子圖（左上角起始位置為(i,j)）。

顯然：，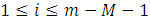

SSDA演算法描述如下：

①定義絕對誤差：

其中，帶有上劃線的分別表示子圖、模板的均值：

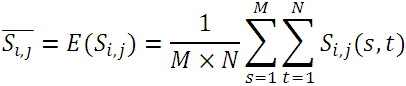
實際上，絕對誤差就是子圖與模板圖各自去掉其均值後，對應位置之差的絕對值。

②設定閾值Th；

③在模板圖中隨機選取不重複的畫素點，計算與當前子圖的絕對誤差，將誤差累加，當誤差累加值超過了Th時，記下累加次數H，所有子圖的累加次數H用一個表R(i,j)來表示。SSDA檢測定義為：

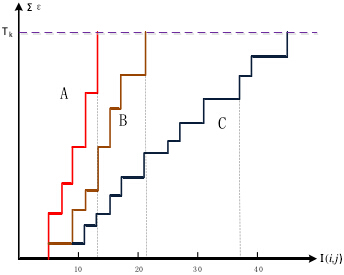
下圖給出了A、B、C三點的誤差累計增長曲線，其中A、B兩點偏離模板，誤差增長得快；C點增長緩慢，說明很可能是匹配點（圖中Tk相當於上述的Th，即閾值；I(i,j)相當於上述R(i,j)，即累加次數）。

④在計算過程中，隨機點的累加誤差和超過了閾值（記錄累加次數H）後，則放棄當前子圖轉而對下一個子圖進行計算。遍歷完所有子圖後，選取最大R值所對應的(i,j)子圖作為匹配影象【若R存在多個最大值（一般不存在），則取累加誤差最小的作為匹配影象】。

        由於隨機點累加值超過閾值Th後便結束當前子圖的計算，所以不需要計運算元圖所有畫素，大大提高了演算法速度；為進一步提高速度，可以先進行粗配準，即：隔行、隔離的選取子圖，用上述演算法進行粗糙的定位，然後再對定位到的子圖，用同樣的方法求其8個鄰域子圖的最大R值作為最終配準影象。這樣可以有效的減少子圖個數，減少計算量，提高計算速度。

——————————————————————————————————————————————————————————————————————

SATD演算法

       hadamard變換演算法（Sum of Absolute Transformed Difference，簡稱SATD演算法），它是經hadamard變換再對絕對值求和演算法。hadamard變換等價於把原影象Q矩陣左右分別乘以一個hadamard變換矩陣H。其中，hardamard變換矩陣H的元素都是1或-1，是一個正交矩陣，可以由MATLAB中的hadamard(n)函式生成，n代表n階方陣。

      SATD演算法就是將模板與子圖做差後得到的矩陣Q，再對矩陣Q求其hadamard變換（左右同時乘以H，即HQH），對變換都得矩陣求其元素的絕對值之和即SATD值，作為相似度的判別依據。對所有子圖都進行如上的變換後，找到SATD值最小的子圖，便是最佳匹配。

MATLAB實現：

1. %//*****************************************   
2. %//Copyright (c) 2015 Jingshuang Hu   
3. %//@filename:demo.m   
4. %//@datetime:2015.08.20   
5. %//@author:HJS   
6. %//@e-mail:[email protected]   
7. %//@blog:http://blog.csdn.net/hujingshuang   
8. %//*****************************************  
9. %%   
10. %//SATD模板匹配演算法-哈達姆變換(hadamard)
11. clear all;  
12. close all;  
13. %%  
14. src=double(rgb2gray(imread('lena.jpg')));%//長寬相等的
15. mask=double(rgb2gray(imread('lena_mask.jpg')));%//長寬相等的
16. M=size(src,1);%//搜尋圖大小
17. N=size(mask,1);%//模板大小
18. %%  
19. hdm_matrix=hadamard(N);%//hadamard變換矩陣
20. hdm=zeros(M-N,M-N);%//儲存SATD值
21. for i=1:M-N  
22.     for j=1:M-N  
23.         temp=(src(i:i+N-1,j:j+N-1)-mask)/256;  
24.         sw=(hdm_matrix*temp*hdm_matrix)/256;  
25.         hdm(i,j)=sum(sum(abs(sw)));  
26.     end  
27. end  
28. min_hdm=min(min(hdm));  
29. [x y]=find(hdm==min_hdm);  
30. figure;imshow(uint8(mask));  
31. title('模板');  
32. figure;imshow(uint8(src));hold on;  
33. rectangle('position',[y,x,N-1,N-1],'edgecolor','r');  
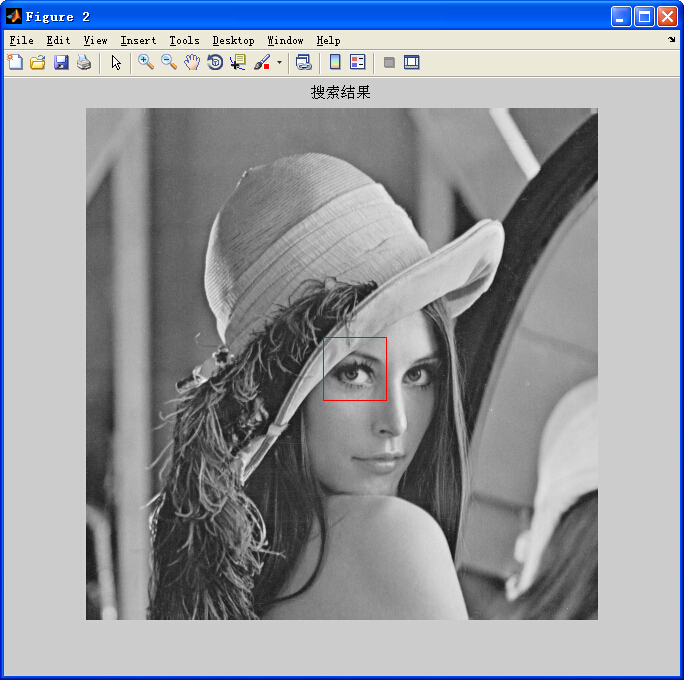
34. title('搜尋結果');hold off;  
35. %//完

輸出結果：

——————————————————————————————————————————————————————————————————