先上號稱最難數獨的解題結果圖

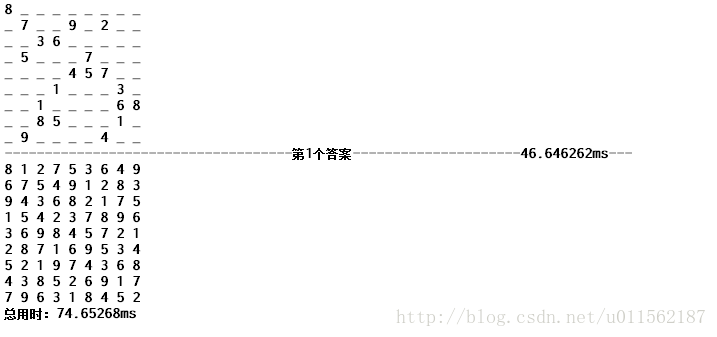
簡單:

其中使用int[9][9]的二維陣列表示數獨各位置的值和候選數：

其中只使用了唯一候選數法和遞迴試填,雖然也寫了其他解題技巧的實現（如隱性唯一候選數法、候選數區塊刪減法、候選數對刪減法、隱性候選數對刪減法等）,加入之後也可以將其變成一個解題演示器，但加入之後：1.時間效率上並不比現在的更高，2.並沒有寫完所有的已知解題技巧的實現，並且，即使寫出了所有解題技巧的實現，遞迴試填仍然是解高階難題必須使用的方法。所以,最後也沒加。

完整程式碼:

package test;

/**
 * @author l.wang([email protected])
 */
public class Sudoku {
    /**
     * 號稱最難數獨( 空格分開的81個數字 0 表示待填,)
     */
    static String source = "8 0 0 0 0 0 0 0 0" +
                           "0 7 0 0 9 0 2 0 0" + 
                           "0 0 3 6 0 0 0 0 0" + 
                           "0 5 0 0 0 7 0 0 0"
 
 +
                           "0 0 0 0 4 5 7 0 0" + 
                           "0 0 0 1 0 0 0 3 0" + 
                           "0 0 1 0 0 0 0 6 8" +
                           "0 0 8 5 0 0 0 1 0" +
                           "0 9 0 0 0 0 4 0 0";
    static long start;
    static int i;

    public static void main(String[] args) {
        start = System.nanoTime();
        int[][] data = init(source);
        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                if (data[i][j] == 0) {
                    data[i][j] = 0x1ff;
                }
            }
        }
        print(data);
        solve(data);
        System.out.println("總用時：" + (System.nanoTime() - start) / 1000000.0 + "ms");
    }

    private static void solve(int[][] data) {
        analyse(data);
        int result = check(data);
        if (result == 1) {
            int[] position = smallPosition(data);
            int pv = data[position[0]][position[1]];
            int pvcount = Integer.bitCount(pv);
            for (int i = 0; i < pvcount; i++) {
                int testV = 1 << ((int) (Math.log(Integer.highestOneBit(pv)) / Math.log(2)));
                pv ^= testV;
//               System.out.println("試填["+position[0]+","+position[1]+"]"+((int)
//               (Math.log(Integer.highestOneBit(testV)) / Math.log(2))+1));
                int[][] copy = copyData(data);
                copy[position[0]][position[1]] = testV;
                solve(copy);
            }
        } else if (result == 0) {
            System.out.println("------------------------------------第"+(++i)+"個答案---------------------"
                    + (System.nanoTime() - start) / 1000000.0 + "ms---");
            print(data);
        }
    }

    /**
     * 複製數獨陣列
     * @param data
     * @return
     */
    private static int[][] copyData(int[][] data) {
        int[][] copy = new int[9][9];
        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                copy[i][j] = data[i][j];
            }
        }
        return copy;
    }

    /**
     * 找到候選數最少的位置開始嘗試<br>
     * <b>****顯著提升了效率*****<b>
     * @param data
     * @return int[2] 行列位置
     */
    public static int[] smallPosition(int[][] data) {
        int[] res = null;
        int smallCount = 10;
        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                int bitcount = Integer.bitCount(data[i][j]);
                if (bitcount == 2) {
                    return new int[] { i, j };
                } else if (bitcount != 1) {
                    if (smallCount > bitcount) {
                        smallCount = bitcount;
                        res = new int[] { i, j };
                    }
                }
            }
        }
        return res;
    }

    /**
     * 檢查結果
     * @param data
     * @return <b>0</b>   正確<br>
     *                  <b>1</b>    還有位置未填<br>
     *                  <b>-1</b>    錯誤<br>
     */
    private static int check(int[][] data) {
        for (int i = 0; i < 9; i++) {
            int row = 0;
            int col = 0;
            int block = 0;
            for (int j = 0; j < 9; j++) {
                if (Integer.bitCount(data[i][j]) > 1) {
                    return 1;
                }
                row |= data[i][j];
                col |= data[j][i];
            }

            for (int h = i / 3 * 3; h < i / 3 * 3 + 3; h++) {
                for (int l = i % 3 * 3; l < i % 3 * 3 + 3; l++) {
                    block |= data[h][l];
                }
            }
            if (row != 0x1ff || col != 0x1ff || block != 0x1ff) {
                return -1;
            }
        }
        return 0;
    }

    private static void analyse(int[][] data) {
        boolean changed = false;
        changed = reduce(data);
        //TODO 還可以加入其它刪減候選數演算法，將這變成一個解題演算器
        if (changed) {
            analyse(data);
        }
    }

    /**
     * 根據行列宮已有值進行簡單的候選數刪減
     * @param data
     * @return
     */
    private static boolean reduce(int[][] data) {
        boolean changed = false;
        for (int m = 0; m < 9; m++) {
            for (int n = 0; n < 9; n++) {
                if (Integer.bitCount(data[m][n]) != 1) {
                    if (setMaybe(data, m, n)) {
                        changed = true;
                    }
                }
            }
        }
        return changed;
    }

    /**
     * 設定m行n列位置的可能值
     * 
     * @param m
     *            行（0-8）
     * @param n
     *            列（0-8）
     * @return 是否減少了候選數
     */
    private static boolean setMaybe(int[][] data, int m, int n) {
        if (Integer.bitCount(data[m][n]) == 1) {
            return false;
        }
        int row = 0;// 行已確定值集合
        int col = 0;// 列已確定值集合
        int block = 0; // 宮格已確定值集合

        for (int i = 0; i < 9; i++) {
            if (Integer.bitCount(data[m][i]) == 1) {
                row += data[m][i];
            }
            if (Integer.bitCount(data[i][n]) == 1) {
                col += data[i][n];
            }
        }

        for (int i = m / 3 * 3; i < m / 3 * 3 + 3; i++) {
            for (int j = n / 3 * 3; j < n / 3 * 3 + 3; j++) {
                if (Integer.bitCount(data[i][j]) == 1) {
                    block += data[i][j];
                }
            }
        }

        int have = row | col | block;// 不可能的值
        int left = 0x1ff ^ have;// 候選數
        // System.out.println("["+m+","+n+"]"+Integer.toBinaryString(left));
        return tryReduce(data, m, n, left);
    }

    /**
     * 新的候選數與老的候選數比較，嘗試減少候選數
     * 
     * @param data
     * @param m
     *            行（0-8）
     * @param n
     *            列（0-8）
     * @param v
     *            候選數，如0x1F9(二進位制1 1111 1001)表示候選數為1 4 5 6 7 8 9
     * @return 是否改變了m行n列的候選數,<br/>
     *         <b>true</b> 減少了候選數<br/>
     *         <b>false</b> 沒有減少
     */
    private static boolean tryReduce(int[][] data, int m, int n, int v) {
        int old = data[m][n];
        data[m][n] = old & v;
        return data[m][n] != old;
    }

    /**
     * 初始化資料
     * 
     * @param source
     *            空格分開的81個數字 0 表示待填
     * @return
     */
    private static int[][] init(String source) {
        source = source.replace(" ", "");
        int[][] data = new int[9][9];
        for (int i = 0; i < source.length(); i++) {
            //應該用source.charAt(i) - '0'
            int v = Integer.parseInt(source.charAt(i) + "");
            if (v != 0) {
                data[i / 9][i % 9] = 1 << (v - 1);
            }
        }
        return data;
    }

    /**
     * 列印數獨
     * 
     * @param data
     */
    private static void print(int[][] data) {
        for (int m = 0; m < 9; m++) {
            for (int n = 0; n < 9; n++) {
                int v = getV9(data[m][n]);
                if (v != -1) {
                    System.out.print(v + " ");
                } else {
                    System.out.print("_ ");
                }
            }
            System.out.println();
        }
    }

    /**
     * 將使用1的位移表示的數字轉換為整數;
     * 
     * @param v
     *            用1的位移表示的數值
     * @return
     */
    public static int getV9(int v) {
        // 使用switch與使用Math.log時間效率差不多
        switch (v) {
        case 1:
            return 1;
        case 2:
            return 2;
        case 4:
            return 3;
        case 8:
            return 4;
        case 16:
            return 5;
        case 32:
            return 6;
        case 64:
            return 7;
        case 128:
            return 8;
        case 256:
            return 9;
        default:
            break;
        }
        return -1;
    }

}