前言：本篇部落格主要講fundamental matrix的由來與推導

9.2 The fundamental matrix F

　　綜合來說fundamental matrix就是epipolar geometry的代數表示，接下來我們從點和它對應的epipolar line來推導F，然後分析這個矩陣的性質。
　　
9.2.1 幾何推導

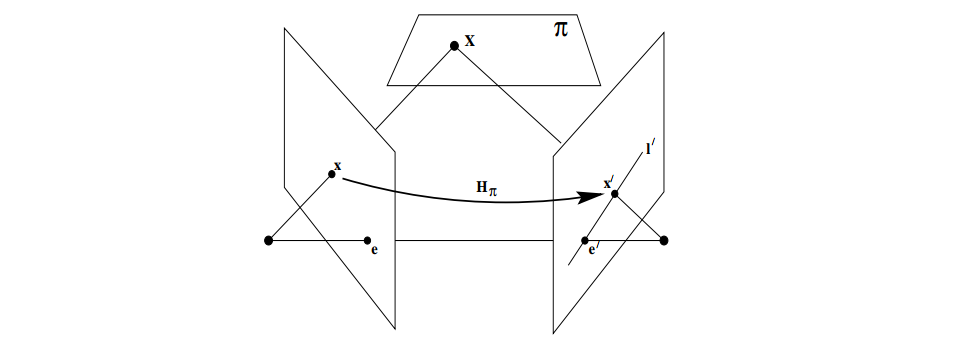
　　我們把從一個點到求出它的對應的epipolar line這個過程分為兩步，第一步，左圖的x被map到右圖的x’，x’經過epipolar line l’，x’是x的一個潛在匹配點，第二步，我們連線x’與e’可以確定l’。

一個不經過相機中心的平面π，一條從左相機中心發出的射線經過x會與π交於點X，X在右圖的投影點是x’，而且x’必定經過l’，同理一系列這樣的點

會對應一系列右圖中的，由於他們都projectively equivalent（投影等價）於Xi，所以存在單應性矩陣H可以把每個x變換到x’。
第二步：構建epipolar line
　　經過右圖x’與e’的直線l’我們可以寫成,中括號加個叉代表反對稱矩陣，舉個例子：如果，那麼
　　　　　　　　　　　　　　　　　　　　　　　　
　　也就是想辦法把叉乘轉化成點乘，又,所以我們有
　　　　　　　　　　　　　　　　　　　　　　　　　　
其中
　　　　　　　　　　　　　　　　　　　　　　　　　　
Hπ就是在π平面上從一個影象平面到另一個影象平面的轉移矩陣，又[e’]x的rank是2，Hπ的rank是3，所以F的rank是2。
　　幾何上來講，F就是從左圖投影平面到一簇epipolar line的轉換矩陣，而且上面牽扯的到的π平面並對於F的存在來說並不是必要的，它只是用來幫助定義從左圖到右圖的點對應關係。
　　
9.2.2 代數推導

　　我們可以通過求解投影方程 PX = x 得到：，P右上角加號代表Ｐ的偽逆矩陣，也就是，Ｃ是相機鏡頭中心，PC = 0，這條直線可以看做λ的引數方程，當λ＝０時這條線經過，當λ＝∞時直線經過Ｃ，這兩個點在右相機（相機矩陣是Ｐ’）的投影分別是和P’C，連線這兩個投影點就得到了epipolar line，P’C就是左相機中心再右圖中的投影（epipole），所以我們得到：
　　　　　　　　　　　　　　　　　　　　　　　　　　
其中
　　　　　　　　　　　　　　　　　　　　　　　　　　
這跟我們上一節推匯出的公式是一致的，單應性矩陣Hπ有著關於兩個相機矩陣P’和P的明確形式：，注意這個公式再兩個相機中心重合時不成立，也就是P’C和PC一樣也為０時。

　　好了，今天公式不少，讀者消化一下吧。