筆記——CNN Architectures(cs231n 斯坦福計算機視覺公開課)
常見的 CNN Architectures
-
LeNet-5
-
AlexNet
-
VGG
-
GoogLeNet
-
ResNet
一些計算:
全連線層、卷積、池化操作對於維度的改變:
Fully Connected Layer:暴力拉平操作,不管原來是什麼樣的長*寬*深。
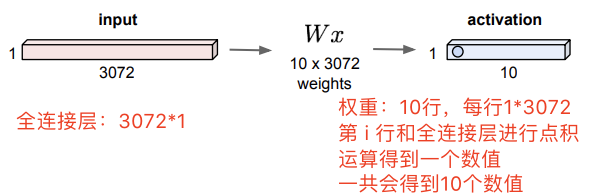
假設上圖是一個分類神經網路的最後兩層,該全連線層連線著輸出層,輸出層給出十個類別的數值。每一行權重都表示一個 template,也就是一個類別,比如貓啊狗啊青蛙啊。
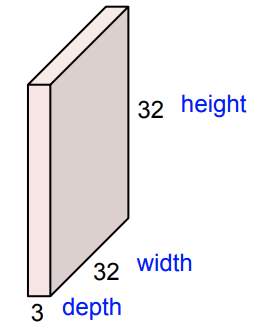
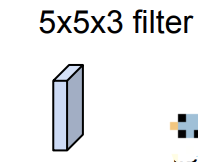
如圖,左邊粉色塊狀,右邊藍色塊狀表示一個卷積核。經過6個
的卷積核後

得到了一個新的 image:
卷積操作後的輸出:
輸入:
濾波器:
個
stride:
輸出:
濾波器:個,一般是
個。
1. LeNet(1998)
架構:
CONV 1 POOL 1 CONV 2 POOL 2 FC 3 FC 4

細節:
卷積核
,stride
池化層
,stride
2. AlexNet (2012,8 layer)
AlexNet 是ImageNet Large Scale Visual Recognition Challenge (ILSVRC)的第一個 基於CNN的第一名。
架構:
CONV1 - MAX POOL1 - NORM1 - CONV2 - MAX POOL2 - NORM2 - CONV3 - CONV4 - CONV5 - Max POOL3 - FC6 - FC7- FC8

CONV1: 96 個 的卷積核,
CONV1的輸入維度: 227x227x3 images
CONV1的輸出維度:即
(提示:
)
CONV1需要學習的引數:
(卷積核的長*寬*深度*數量,深度取決於影象的深度)
(卷積核是需要學習的,96個卷積核一種有多少個數值就是多少個需要被學習的引數)
Note:卷積層CONV1會改變輸出維度的深度,深度為卷積核的數量。因為每一個卷積核都會輸出一個
的 feature map,這些 feature map 是疊放的,構成新的深度。
MAX POOL1: ,
MAX POOL1的輸入維度:
MAX POOL1的輸出維度:
(相當於對 CONV1層得到的每一個 feature map 做 pooling)
POOL1需要學習的引數:0個
Note:池化層MAX POOL1不會改變輸出維度的深度。
具體維度如下:
| INPUT | [227x227x3] | ||
| CONV1 | [55x55x96] | 96 11x11 filters at stride 4 | pad 0 |
| MAX POOL1 | [27x27x96] | 3x3 filters at stride 2 | |
| NORM1 | [27x27x96] | Normalization layer | |
| CONV2 | [27x27x256] | 256 5x5 filters at stride 1 | pad 2 |
| MAX POOL2 | [13x13x256] | 3x3 filters at stride 2 | |
| NORM2 | [13x13x256] | Normalization layer | |
| CONV3 | [13x13x384] | 384 3x3 filters at stride 1 | pad 1 |
| CONV4 | [13x13x384] | 384 3x3 filters at stride 1 | pad 1 |
| CONV5 | [13x13x256] | 256 3x3 filters at stride 1 | pad 1 |
| MAX POOL3 | [6x6x256] | 3x3 filters at stride 2 | |
| FC6 | [4096] | 4096 neurons | |
| FC7 | [4096] | 4096 neurons | |
| FC8 | [1000] | 1000 neurons (class scores) |
3. VGG(2014,19 layer)
和AlexNet 相比,VGG 採用的是更小的卷積核,網路也更深。

VGG 僅採用 3x3, stride 1,pad 1的卷積層, 2x2, stride 2的最大池化層。
那麼就有一個問題就Q:為什麼VGG 採用更小的卷積核?
從感受野的等效性、引數數量、網路深度的角度來看
3個,stride
的卷積核的感受野等於一個
的卷積核,如下圖所示(畫圖果然是理清思路的利器啊利器)。

從感受野的等效性、引數數量、網路深度三個角度來比較,如下表:
| 3x3的卷積核 | 1x1的卷積核 | |
| 相同感受野(7個輸入) | 3個 | 1個 |
| 引數量 | ||
| 深度 | 3 | 1 |
深度越深,就加入了更多的非線性,大概對神經網路來說是很好的。
持續更新中......
