人們都說決策樹是一種很簡單的分類器，筆者也看過不少關於決策樹的文章以及教程之類的，可是如果你讓把獨立地把這個決策過程完整地複述一遍，還是會有很多細節不太明瞭。在這裡以問答形式作一個總結，錯誤的地方請指正。

一 你能說說決策樹的基本流程嗎？
顧名思義，決策樹就是以一種樹形的結構來對問題做判斷。比如‘我們要決定明天要不要去桂林旅遊’這個問題，首先我們會看看‘有合適的車票嗎’，如果有，那再看看’有合適的住宿嗎‘，如果有，那再看看’明天天氣好嗎‘，如果好，那再看看’那邊有什麼好吃的麼‘， 如果有，那我們就決定去桂林吧。當然，這只是我個人的決策過程。可能有些人把’有沒有好吃的‘放在第一位，有的人把‘風景是不是好看’放在第一位，有的人即使沒有合適的天氣也會想去逛逛。
簡而言之，決策樹按照分而治之的方法，每一次根據某個屬性的值對樣本進行分類，再傳遞給下一個屬性進行判斷分類。越早用於分類的屬性所分類的樣本數量越多，對分類結果的影響越大。

二 那什麼時候終止分類呢？
直至所有訓練資料子集被基本正確的分類，或者沒有合適的屬性為止

三 在每個當前結點，應該怎麼選取屬性？
有三種方法來選取屬性：
ID3：資訊增益 ＝ 樣本集的資訊熵－考慮某一屬性之後的資訊熵。資訊增益越大，我們就可以認為這個屬性對分類的結果影響越大，這裡便取使得資訊增益最大的屬性。但是，這種方法會對屬性取值多的屬性有偏好。試想，我們把每個樣本的ID也作為屬性參與到分類任務中，它對應的資訊增益很大，而通過ID屬性的劃分，每個屬性取值下便只有一個樣本，那這個‘樣本集’顯然是不能再作分類了。為了減少這種不利影響，便有了C4.5方法。
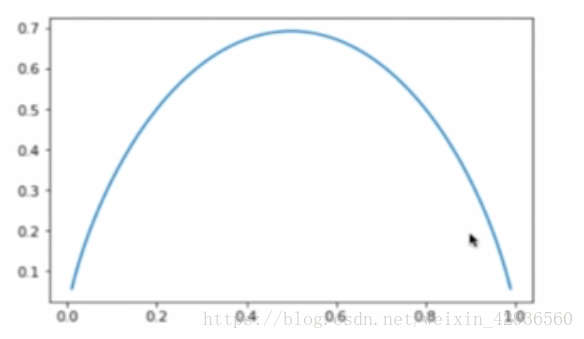
下面我們用程式碼演示一下資訊熵的運算(這裡演示的是一個二分類問題，概率不同時不同的資訊熵，可以看到，當兩個類別的出現概率一樣時，資訊熵最大，也就是說不確定性越大)：

import numpy as np
import matplotlib.pyplot as plt
def entropy(p):
    return = -p*np.log(p)-(1-p)*np.log(1-p)
x = np.linspace(0.01,0.99,200)
plt.plot(x,entropy(x))
plt.show()

C4.5：資訊增益率 ＝ 資訊增益/屬性的固有熵。屬性的值越多，屬性的固有熵就越大，相當於對ID3的方法作了一個懲罰的作用。另外，需要注意的是，單純考慮資訊增益率偏向於選擇屬性值少的特徵，所以實際上，我們會先找出資訊增益高於平均水平的屬性，再從中選擇增益率最高的。

CART：基尼指數：從根據某一屬性分類後的樣本集中任意取兩個樣本，其類別標記不一致的概率，基尼指數越小，說明樣本集的純度越高。
公式如下：

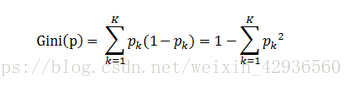
具體計算流程可以參考這篇文章：https://www.cnblogs.com/muzixi/p/6566803.html

四 如果某個屬性是連續值，那應該怎麼辦呢？
比如，有20個樣本，包含溫度這個屬性，有很多取值，總不能每一種取值下作一個分類吧？！在這裡我們要取其中一個值作為劃分的閥門，比如大於30度就是熱，小於30度就是不熱。那怎麼找這個值呢？可以逐個選取在樣本集中的溫度取值作為劃分閾值，計算哪個值的分類效果最好便取哪個值作為閾值。

五 在有些樣本中有些屬性值缺失的情況下如何選擇劃分屬性？
以計算某個屬性的資訊增益為例，選取此屬性不缺失的樣本計算資訊增益，再乘以屬性不缺失的樣本相對於總樣本量的概率

六 選好了劃分屬性，某個樣本若缺失此屬性值，應該劃分到哪個結點去呢？
劃分到各個結點，但是要乘以相應的權重，權重值為某結點的樣本數相對於總樣本量的概率

七 決策樹都有什麼優缺點？
過程簡單明瞭，特別直觀可解釋性強；
對缺失值不敏感；
容易過擬合；
如果有新的樣本加入，必須重新建立一棵決策樹

八 怎麼對決策樹容易過擬合這個問題進行處理？
決策樹生成演算法遞迴的產生決策樹，直到不能繼續下去為止，這樣產生的樹往往對訓練資料的分類很準確，但對未知測試資料的分類缺沒有那麼精確，即會出現過擬合現象。過擬合產生的原因在於在學習時過多的考慮如何提高對訓練資料的正確分類，從而構建出過於複雜的決策樹，解決方法是考慮決策樹的複雜度，對已經生成的樹進行簡化，稱作剪枝。
剪枝：從已經生成的樹上裁掉一些子樹或葉節點，並將其根節點或父節點作為新的葉子節點，從而簡化分類樹模型。
決策樹的代價函式：Ｌ＝ 各個結點的經驗熵＊結點的樣本樹＋懲罰係數＊結點個數
懲罰係數越大，結點個數就越少，那麼決策樹便越簡單。

九 隨機森林是怎麼回事？
隨機森林，顧名思義，就是有許多決策樹的分類器集合，包含兩個隨機過程：
隨機選取樣本，訓練決策樹；
隨機選取屬性，訓練決策樹
訓練得到一事實上數量的決策樹之後，對於新的輸入資料，用投票表決法得到最終的分類結果