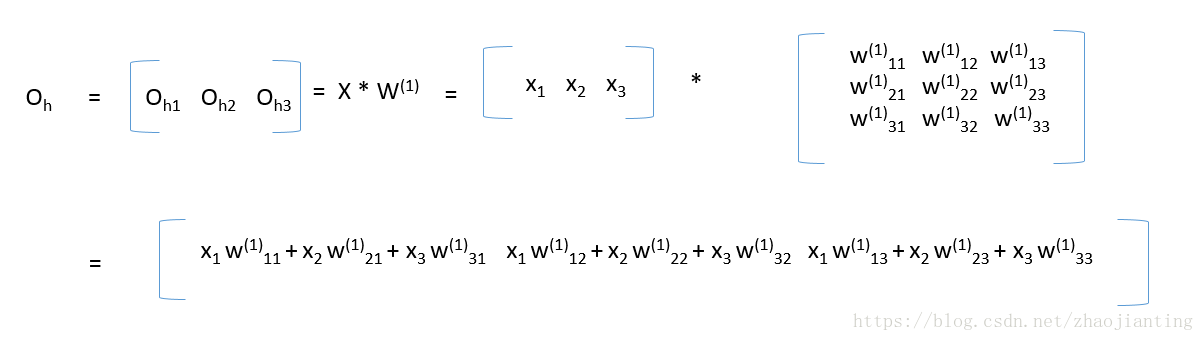神經網路一之神經網路結構與原理以及python實戰
技術交流qq群: 659201069
本系列埔文由淺入深介紹神經網路相關知識,然後深入神經網路核心原理與技術,最後淺出python神經網路程式設計實戰。通過本系列博文,您將徹底理解神經網路的原理以及如何通過python開發可用於生產環境的程式。本博文論討神經網路的結構與原理
計算機所長:
瞭解計算機源理的人都知道計算機只適合做與之相匹配的任務(計算機只能執行0和1的二制機加法),如數學計算、繪製圖表,目前的計算機每秒可以執行10數量級的加法運算,但是計算機也有軟肋,下面幾張簡單的數字圖片,人類很容易識別,但計算機卻很難識別出來。
人類所長:
對於上面幾副圖片,我們快速準確的識別出圖片上的內容。我們人類可以識別複雜圖片上的大量資訊,但計算機卻很難做到。
人工智慧:
每秒幾十億次計算能力的計算機卻識別不出圖片中的幾個數字,這是因為人類具有思維能力。但時人們想利用計算機的快速運算、進行圖片識別之類的功能,這就是人工智慧要解決的問題。
人類思維過程:

我們從眼睛輸入圖片、耳朵輸入音樂,經過大腦分析,最後給出答案
計算機模仿人類思維過程:
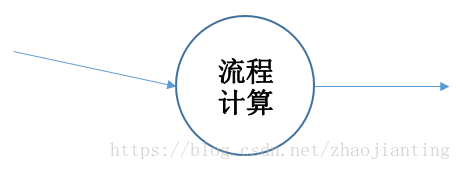
計算機只能拿到圖片的畫素,也就是隻能拿到一系列的0和1的陣列,而且計算機不能思考只能執行程式設計師預先設定好的流程,最後給出答案,本文要討論的就是上圖計算機的“流程計算”如何實現人類的智慧。
神經元:

神經元接受電訊號,從一個神經元傳到別一個神經元,這就是身體感知光、聲、電、熱等訊號的機制。電訊號最到傳到大腦,而大腦本身也就由神經元組成的。神經元接受大訊號後不會立即反應而是抑制輸放,直接訊號強度達到一個預閾值,才會產生輸出(後面的沒啟用函式就是模仿神經元的這個功能)。
計算機的神經元實現:
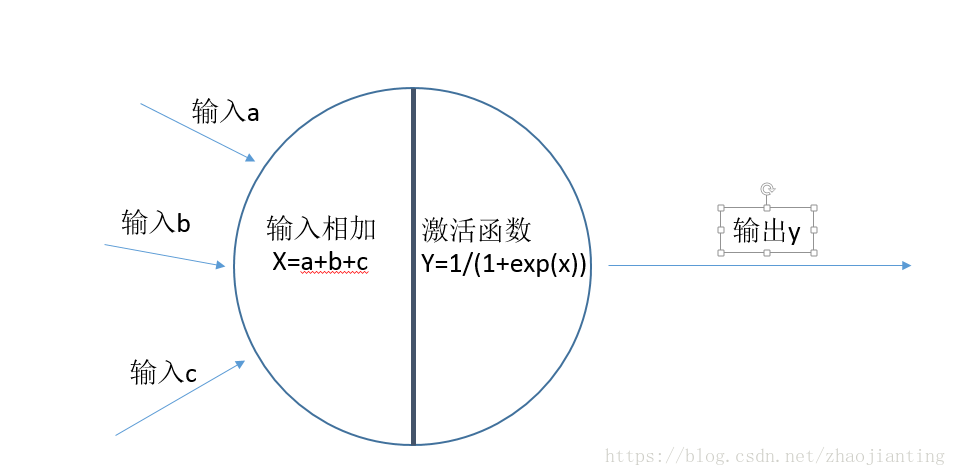
神經元可以接受多個輸入,然後對它們相加,作為啟用函式的輸入,啟用函式最後給出輸出。這就是神經網路的核心神經元的主要原理。啟用函式現在有好多個,我們採用S函式(後面的博文再專門討論啟用函式),影象如下:
神經網路結構與原理
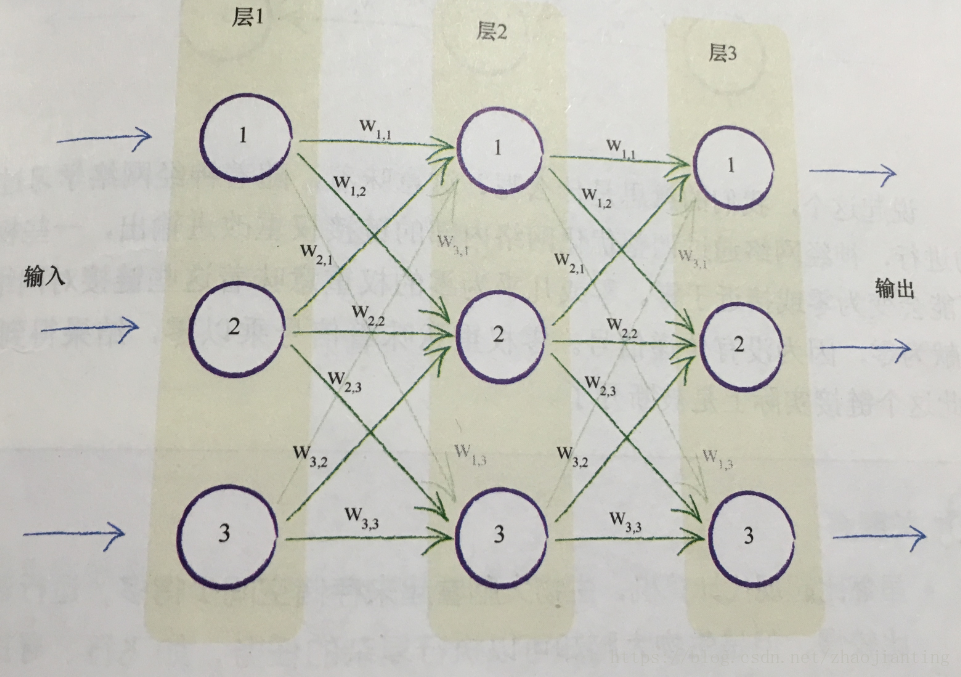
神經網路就是由分成多層的多個神經元組成(現在的神經網路可以達到百層以上)。每個層中的每個神經元都與其前後層的神經元互連,這種網路結構稱全連線神經網路,這是經典的神經網路也就應用最多的神經網路。當然後面又了出現了卷積神經網路,在此不做討論。
上面的神經網路分三層,分層由三個神經元,每個神經元的間的連線都有都有一個權重,較大的權重給加經輸入,較小的會弱化輸入。
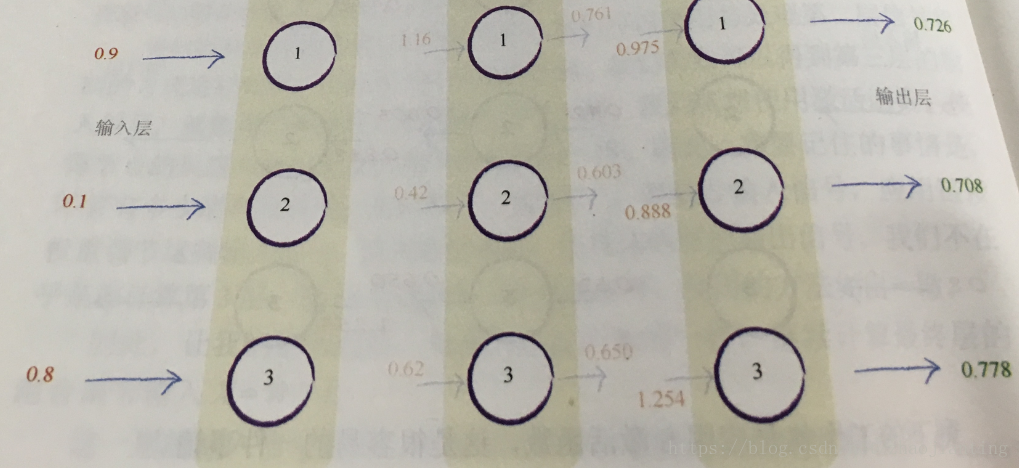
看下圖展示了輸入訊號在神經網路的整個傳輸過程
輸入為
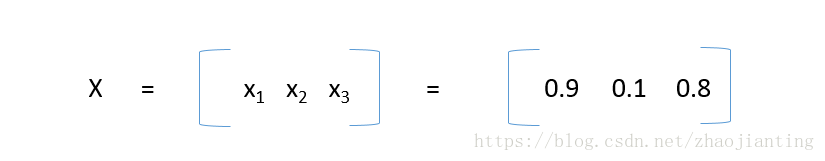
也就是第一層第一個節點輸放為0.9,第一層第二個節點輸放為0.1,第一層第三個節點輸放為0.8
第一層和第二層的連線權重為,也就是第一層第一個節點和第二層第二個節點連連權重為0.9,其它類似,這樣表示是了為後面應用距陣進行計算
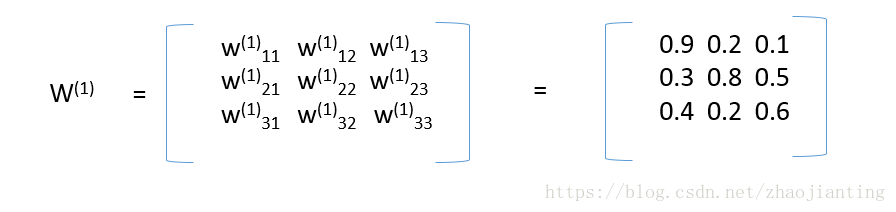
第二層和第三層的連線權重為:
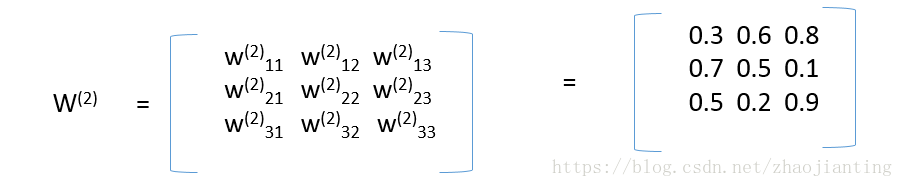
最後的出為

下面我們來分析下0.726是怎麼計算出來的。下面再看下帶權重的神經元結構:
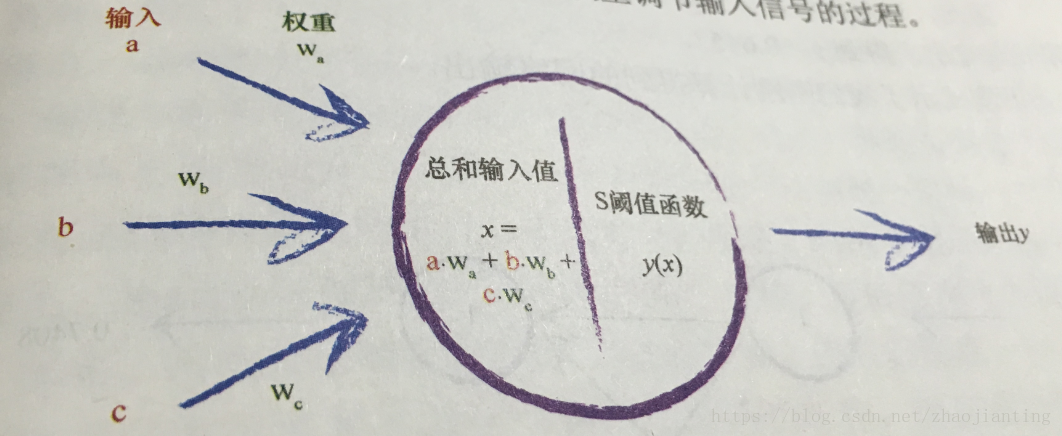
輸入I經過第一層直接輸出原始的輸入。所以第二層節點1的輸入為I = [
0.9
0.1
0.8
]
這是a=0.9,b=0.1,c=0.8,Wa=0.9,Wb=0.3,Wc=0.4,也就是x=0.9*0.9+0.1*0.3+0.8*0.4=1.16,然後應用啟用函式S,即y=S(X)=1/(1+exp(-1.16)) = 0.761,同理可計算第二層其它兩個節點的輸出,最為第二層的輸放為:OH=[
第三層的輸放計算方法和上面第二層的是一樣的。下面看下應用矩陣的計算公式,我們分析下隱藏層和輸出層各們結果的計算結果正好符合下面的矩陣乘法公式(真是無巧不成書,科學就是在巧合中一步步前進),矩陣乘法完成後,然後對每一個元素應用啟用函式即可
第三層的輸出也是同樣的道理,第三輸的輸入為隱藏層的輸出,矩陣乘法完成後,再對每一個元素應用啟用函式即可
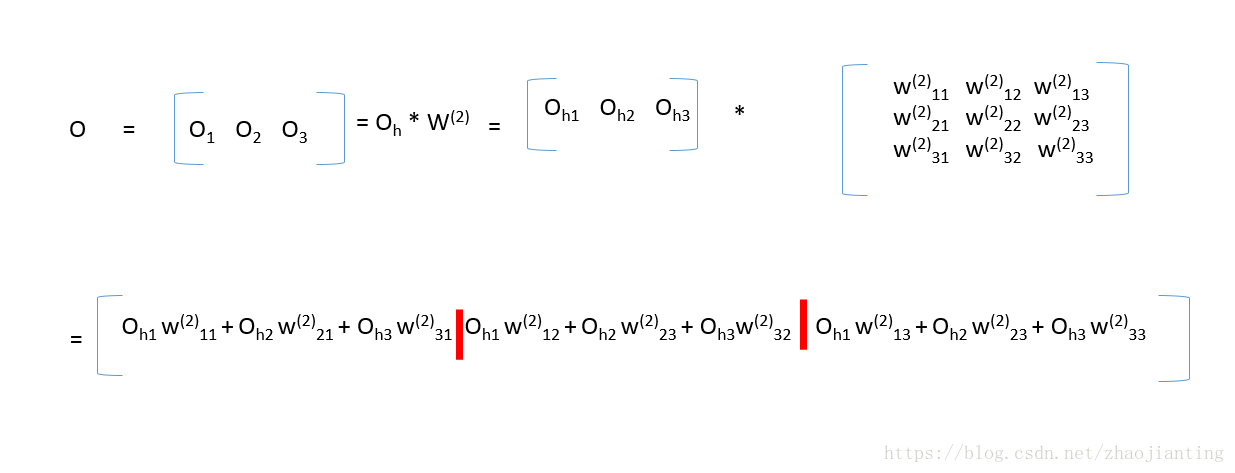
第一層稱為輸放層,最後一層稱為輸出層,中間層統稱為隱藏層,無論神經網路有多少層,計算方法和上面介紹的是一樣的。一開始隨機得到w權重矩陣,最後根據樣本一步步優化w權重矩陣。
下面是python實現的上面所討論的三層神經網路結構:
import numpy
# python中sigmoid函式是 scipy.special.expit
import scipy.special
#三層神經網路結構定義
class neuralNetwork:
# 初始化函式,
#inputnodes輸入層節點數目
#hiddennodes隱藏層節點數目
#outputnodes輸出層節點數目
#learningrate學習率,在訓練時會用到,關於學習率的設定後面的文章再討論
def __init__(self, inputnodes, hiddennodes, outputnodes, learningrate):
self.inodes = inputnodes
self.hnodes = hiddennodes
self.onodes = outputnodes
# wih代表輸入層和隱藏層間的連線矩陣
# who代表隱藏層和輸出層間的連線矩陣
#權重矩陣一般隨機得到,但不要初始化為0和相同的值,具體的初始化方法後面會討論
self.wih = numpy.random.normal(0.0, pow(self.inodes, -0.5), (self.hnodes, self.inodes))
self.who = numpy.random.normal(0.0, pow(self.hnodes, -0.5), (self.onodes, self.hnodes))
self.lr = learningrate
# 啟用函式y=1/(1+exp(-x))
self.activation_function = lambda x: scipy.special.expit(x)
pass
# 查詢函式,也就是由輸入給出輸出
#input_list是輸入層的矩陣,注意格式和維度要正確
def query(self, inputs):
# 輸入有
#下面兩行是計算隱藏層的輸出
hidden_inputs = numpy.dot(inputs, self.wih)
hidden_outputs = self.activation_function(hidden_inputs)
#下面兩行是計算最後的輸出
final_inputs = numpy.dot(hidden_outputs, self.who)
final_outputs = self.activation_function(final_inputs)
return final_outputs