在看到輾轉相除法的遞迴解法後，不禁想到涉及比較的分治演算法、三目運算子和遞迴簡直就是絕配，一眨眼，腦海中就迸出了數列最小值的遞迴解法，每一個數都與後面陣列的最小值相比較，思路有了，動手吧。

1. //輾轉相除法
2. int gcd_division(int a,int b)  
3. {  
4.     return b==0?a:gcd_division(b,a%b);   
5. }  

一、思路與改進

    將陣列每一個元素與該元素後陣列最小值相比較，最後一個數組元素返回自身，即可得到整個陣列的最小值。圖示如下：

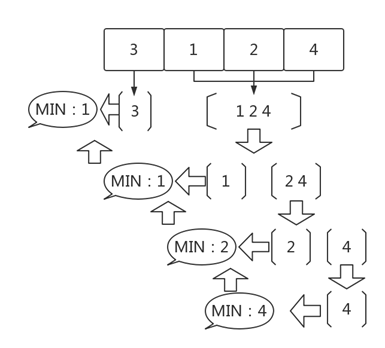
轉化成程式碼就是這樣一個函式：

1. //arr[]:陣列  len:陣列長度    n:
   當前下標
2. int f(int arr[],int len,int n)  
3. {  
4.     if(n == len-1)  
5.         return arr[n];  
6.     return arr[n]<f(arr,len,n+1)?arr[n]:f(arr,len,n+1);  
7. }  

   跑一遍：

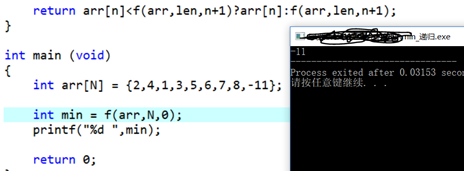
沒問題，不過這遞迴把f(arr,len,n+1)算了兩遍，效率太低了，得改。先求結果，再把結果放入return裡。程式碼如下：

1. //arr[]:陣列  len:陣列長度    n:當前下標
2. int f(int arr[],int len,int n)  
3. {  
4.     if(n == len-1)  
5.         return arr[n];  
6.     int min = f(arr,len,n+1);  
7.     return arr[n]<min?arr[n]:min;  
8. }  

   ok，效率提升了，不過這樣的話，三目運算子就只剩下一個比較的操作了，可以再精簡一下，定義一個比較元素的巨集：MIN(X,Y)

9. #define MIN(X,Y) ((X<Y)?(X):(Y))

改一下return裡的語句：

1. //arr[]:陣列  len:陣列長度    n:當前下標
2. int f(int
    arr[],int len,int n)  
3. {  
4.     if(n == len-1)  
5.         return arr[n];  
6.     int min = f(arr,len,n+1);  
7.     return MIN(min,arr[n]);  
8. }  

   搞定~

原始碼：

1. #include <stdio.h>
2. #define N 10
3. #define MIN(X,Y) ((X<Y)?(X):(Y))
4. int f(int arr[],int len,int n)  
5. {  
6.     if(n == len-1)  
7.         return arr[n];  
8.     int min = f(arr,len,n+1);  
9.     return MIN(min,arr[n]);  
10. }  
11. int main (void)  
12. {  
13.     int arr[N] = {2,4,1,3,5,6,7,8,-11};  
14.     int min = f(arr,N,0);  
15.     printf("%d ",min);  
16.     return 0;  
17. }