題目背景

題目描述（本題是提高組第二題難度＋）

題目描述

\(LJJ\)又要開始上數學課啦！（\(T1\)，永恆不變的數學）

\(LJJ\)的\(Teacher\)對上次的考試很不滿意（其實是出題人對上次的分數那麼高不滿意啦），決定在出一道難（\(water\)）題。

\(LJJ\)的\(Teacher\)給了\(LJJ\)一個數列，但這由於是\(LJJ\)的\(Teacher\)發明的，我們不稱呼他為\(LJJ\)數列，而稱他為\(Teacher\)數列。但是\(LJJ\)還停留在數數的階段啊，所以不能太難。

於是\(LJJ\)的\(Teacher\)隨便給出了一個\(Teacher\)

Teacher會對這個數列進行兩個操作：

1：將其中的一個數加上s（s為整數）

2：Teacher會給出left和right，讓你求：

a[left](right-left+1) + a[left+1](right-left)

• ...... + a[right-1]2 + a[right]1 的值。

即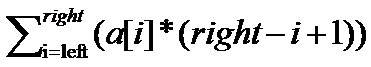

\(LJJ\)的指頭掰不過來了呀，就請您來完成啦~

輸入輸出格式

輸入格式：

第一行有\(2\)個數\(n,q\)，分別表示\(Teacher\)數列中數的個數以及操作次數。

接下來的一行有\(n\)個數，第\(i\)個數表示\(a[i]\)。

再接下來\(q\)

注意：\(Teacher\)數列中的數並不一定都是正數，但一定都是整數。

輸出格式：

對於每一個詢問\((order=2)\)輸出所求答案

輸入輸出樣例

輸入樣例#1：

5 3
2 4 1 3 5
2 2 4
1 2 3
2 2 4

輸出樣例#1：

17
26

說明

資料範圍

\(n \leq 100000, q \leq 100000\)

樣例解釋

\(4*3+1*2+3*1=17\)

\(7*3+1*2+3*1=26\)

提示 \(1\).如果看不懂題目，那麼看這裡：給你一段數列，有兩種操作，單點修改和區間查詢。查詢\(left\)到\(right\)，返回的值是

\(a[left]*(right-left+1)+a[left+1]*(right-left)+...+a[right]*1\)。

2.從另一個角度去想問題，把區間答案劃分開來，否則你會打得很累。

3.題目中說是單點修改，而不是區間修改，有沒有覺得簡單得不可思議呢？

思路：把題目給的式子化一化，提出後面的\(right-1\)，變成\(a_{i}*(right+1)-a_{i}*i\)，整個式子變成\(\sum_{}(a_{i}*(right+1)-a_{i}*i)\)，用樹狀陣列所以維護\(a_{i}*i\)和普通的加法和就好了。

程式碼：

#include<cstdio>
#include<cctype>
#define maxn 100007
#define lb(x) x&(-x)
#define ll long long
using namespace std;
ll n,m,a[maxn],b[maxn];
inline ll qread() {
  char c=getchar();ll num=0,f=1;
  for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
  for(;isdigit(c);c=getchar()) num=num*10+c-'0';
  return num*f;
}
inline void add(ll x, ll w) {
  ll p=x*w;
  while(x<=n) {
    a[x]+=w;
    b[x]+=p;
    x+=lb(x);
  }
}
inline ll csum1(ll x) {
  ll ans=0;
  while(x) {
    ans+=a[x];
    x-=lb(x);
  }
  return ans;
}
inline ll csum2(ll x) {
  ll ans=0;
  while(x) {
    ans+=b[x];
    x-=lb(x);
  }
  return ans;
}
int main() {
  n=qread(),m=qread();
  for(ll i=1,x;i<=n;++i) {
    x=qread();
    add(i,x);
  }
  for(ll i=1,k,l,r;i<=m;++i) {
    k=qread(),l=qread(),r=qread();
    if(k==1) add(l,r);
    else printf("%lld\n",(r+1)*(csum1(r)-csum1(l-1))-csum2(r)+csum2(l-1));
  }
  return 0;
}