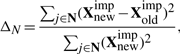介紹

對於處理現實中的資料時，我們常常會遇到缺失值，這裡我們將介紹一種缺失值的填補方法missForest，這是利用隨機森林來填補缺失值的非引數方法，他可以適用於任何型別的資料(連續、離散)。其他類似的缺失值填補方法還有MICE，在這裡不做介紹。

方法

我們假設我們的資料是X=(X1,X2,...,Xp)的n*p的一個矩陣。如果對於一個任意的變數Xs，我們想填充他的缺失值，我們可以將資料分成4部分：
1.用y(s)obs表示Xs的觀測值。
2.用y(s)mis表示Xs的缺失值。
3.用x(s)obs表示Xs以外的觀測值。
4.用x(s)mis表示Xs以外的缺失值。

我畫了一個圖，可以幫助大家更好的理解這4個部分的組成：

紅色部分就是y(s)obs，黃色部分是y(s)mis，綠色部分是x(s)obs，藍色部分是x(s)mis。
接來下我們只需要使用隨機森林，訓練出y~x的模型，然後將缺失值預測出來就可以了，但是不只是Xs存在缺失值，其他變數也是有可能存在缺失值的，這時候我們可以通過迭代的方式來求解。
我們先對缺失值做一個初始的猜測，比如用均值/中位數填充，然後按照變數的缺失率，從小到大排序，先對缺失率小的變數使用隨機森林迴歸從而填補該變數的缺失值，然後一直迭代，直到最新的一次填補結果與上一次的填補結果不再變化（變化很小）時停止。

具體虛擬碼在這裡：

這裡的收斂指標是迭代中缺失值變化的大小，對於連續型變數，我們有：

對於離散型變數：

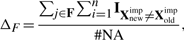
其中#NA是在離散變數中的總的缺失值數量。

R語言實現應用

我們可以使用R包：missForest 來應用這一方法：
以下是一個使用例子：

> library(missForest)
> set.seed(81)
> iris.mis <- prodNA(iris, noNA = 0.2) #產生20%缺失值
> summary(iris.mis)
  Sepal.Length    Sepal.Width     Petal.Length    Petal.Width          Species  
 Min.   :4.300
 
   Min.   :2.000   Min.   :1.100   Min.   :0.100   setosa    :40  
 1st Qu.:5.200   1st Qu.:2.800   1st Qu.:1.600   1st Qu.:0.300   versicolor:38  
 Median :5.800   Median :3.000   Median :4.450   Median :1.300   virginica :44  
 Mean   :5.878   Mean   :3.062   Mean   :3.905   Mean   :1.222   NAs      :28  
 3rd Qu.:6.475   3rd Qu.:3.300   3rd Qu.:5.100   3rd Qu.:1.900                  
 Max.   :7.900   Max.   :4.400   Max.   :6.900   Max.   :2.500                  
 NAs   :28      NAs   :29      NAs   :32      NAs   :33  

> iris.imp <- missForest(iris.mis, verbose = TRUE)
> iris.imp$ximp #修補後的資料

> head((iris.imp$ximp-iris)[,1:4])
  Sepal.Length Sepal.Width Petal.Length Petal.Width
1   0.00000000     0.00000   0.00000000  0.00000000
2   0.00000000     0.30825   0.00000000  0.02720000
3   0.00000000     0.00000   0.00000000  0.00000000
4   0.00000000     0.22050  -0.03142857  0.00000000
5   0.00000000     0.00000   0.00000000  0.00000000
6   0.01766667     0.00000   0.00000000 -0.02533333

可以看到修補的資料與原資料想減，我們就可以清楚的看到這個效果是很不錯的，如果我們僅僅使用均值這樣的填充方法，就不能夠這麼準確了。

當然這方法雖然效果比較好，但是相比均值填充的方法來講，效率就太低了，如果資料量比較大的話，這個方法會很慢，至於如何使用，就看各位自己的取捨了。

參考文獻：

作為分享主義者(sharism)，本人所有網際網路釋出的圖文均遵從CC版權，轉載請保留作者資訊並註明作者a358463121專欄:http://blog.csdn.net/a358463121，如果涉及原始碼請註明GitHub地址：https://github.com/358463121/。商業使用請聯絡作者。