C++小知識(九)——Eigen庫的基本使用方法、PCL計算協方差矩陣
轉載自:https://blog.csdn.net/r1254/article/details/47418871
以及https://blog.csdn.net/wokaowokaowokao12345/article/details/53397488
第一部分:
1.1前言
Eigen是一個高層次的C ++庫,有效支援 得到的線性代數,矩陣和向量運算,數值分析及其相關的演算法。
1.2配置
關於Eigen庫的配置只需要在屬性表包含目錄中新增Eigen路徑即可。
1.3例子
Example 1:
#include <iostream> #include <Eigen/Dense> void main() { Eigen::MatrixXd m(2, 2); //宣告一個MatrixXd型別的變數,它是2*2的矩陣,未初始化 m(0, 0) = 3; //將矩陣第1個元素初始化3 m(1, 0) = 2.5; //將矩陣第3個元素初始化3 m(0, 1) = -1; m(1, 1) = m(1, 0) + m(0, 1); std::cout << m << std::endl; }
Eigen標頭檔案定義了很多型別,但對於簡單的應用程式,可能只使用MatrixXd型別。 這表示任意大小的矩陣(MatrixXd中的X),其中每個條目是雙精度(MatrixXd中的d)。 Eigen / Dense標頭檔案定義了MatrixXd型別和相關型別的所有成員函式。 在這個標頭檔案中定義的所有類和函式都在特徵名稱空間中。
Example 2:
#include <iostream> #include <Eigen/Dense> using namespace Eigen; using namespace std; int main() { MatrixXd m = MatrixXd::Random(3,3); //使用Random隨機初始化3*3的矩陣 m = (m + MatrixXd::Constant(3,3,1.2)) * 50; cout << "m =" << endl << m << endl; VectorXd v(3); //這表示任意大小的(列)向量。 v << 1, 2, 3; cout << "m * v =" << endl << m * v << endl; }
#include <iostream> #include <Eigen/Dense> using namespace Eigen; using namespace std; int main() { Matrix3d m = Matrix3d::Random(); //使用Random隨機初始化固定大小的3*3的矩陣 m = (m + Matrix3d::Constant(1.2)) * 50; cout << "m =" << endl << m << endl; Vector3d v(1,2,3); cout << "m * v =" << endl << m * v << endl; }
Matrix&Vector
Example 3:
#include <iostream>
#include <Eigen/Dense>
using namespace Eigen;
int main()
{
MatrixXd m(2,2);
m(0,0) = 3;
m(1,0) = 2.5;
m(0,1) = -1;
m(1,1) = m(1,0) + m(0,1);
std::cout << "Here is the matrix m:\n" << m << std::endl;
VectorXd v(2);
v(0) = 4;
v(1) = v(0) - 1;
std::cout << "Here is the vector v:\n" << v << std::endl;
}逗號初始化
Example 4:
Matrix3f m;
m << 1, 2, 3, 4, 5, 6, 7, 8, 9;
std::cout << m;通過Resize調整矩陣大小
矩陣的當前大小可以通過rows(),cols()和size()檢索。 這些方法分別返回行數,列數和係數數。 通過resize()方法調整動態大小矩陣的大小。
Example 5:
#include <iostream>
#include <Eigen/Dense>
using namespace Eigen;
int main()
{
MatrixXd m(2,5); //初始化大小2*5
m.resize(4,3); //重新調整為4*3
std::cout << "The matrix m is of size " << m.rows() << "x" << m.cols() << std::endl;
std::cout << "It has " << m.size() << " coefficients" << std::endl;
VectorXd v(2); v.resize(5);
std::cout << "The vector v is of size " << v.size() << std::endl;
std::cout << "As a matrix, v is of size " << v.rows() << "x" << v.cols() << std::endl;
}通過賦值調整矩陣大小
Example 6:
MatrixXf a(2, 2);
std::cout << "a is of size " << a.rows() << "x" << a.cols() << std::endl;
MatrixXf b(3, 3);
a = b;
std::cout << "a is now of size " << a.rows() << "x" << a.cols() << std::endl;Eigen + - * 等運算
Eigen通過通用的C ++算術運算子(例如+, - ,)或通過特殊方法(如dot(),cross()等)的過載提供矩陣/向量算術運算。對於Matrix類(矩陣和向量) 只被過載以支援線性代數運算。 例如,matrix1 matrix2表示矩陣矩陣乘積。
Example 7:
#include <iostream>
#include <Eigen/Dense>
using namespace Eigen;
int main()
{
Matrix2d a; a << 1, 2, 3, 4;
MatrixXd b(2,2);
b << 2, 3, 1, 4;
std::cout << "a + b =\n" << a + b << std::endl;
std::cout << "a - b =\n" << a - b << std::endl;
std::cout << "Doing a += b;" << std::endl;
a += b;
std::cout << "Now a =\n" << a << std::endl;
Vector3d v(1,2,3);
Vector3d w(1,0,0);
std::cout << "-v + w - v =\n" << -v + w - v << std::endl;
}Example 8:
#include <iostream>
#include <Eigen/Dense>
using namespace Eigen;
int main()
{
Matrix2d a;
a << 1, 2, 3, 4;
Vector3d v(1,2,3);
std::cout << "a * 2.5 =\n" << a * 2.5 << std::endl;
std::cout << "0.1 * v =\n" << 0.1 * v << std::endl;
std::cout << "Doing v *= 2;" << std::endl; v *= 2;
std::cout << "Now v =\n" << v << std::endl;
}矩陣轉置、共軛和伴隨矩陣
MatrixXcf a = MatrixXcf::Random(2,2);
cout << "Here is the matrix a\n" << a << endl;
cout << "Here is the matrix a^T\n" << a.transpose() << endl;
cout << "Here is the conjugate of a\n" << a.conjugate() << endl;
cout << "Here is the matrix a^*\n" << a.adjoint() << endl;禁止如下操作:
a = a.transpose(); // !!! do NOT do this !!!但是可以使用如下函式:
a.transposeInPlace();此時a被其轉置替換。
#include <iostream>
#include <Eigen/Dense>
using namespace Eigen;
int main()
{
Matrix2i a;
a << 1, 2, 3, 4;
std::cout << "Here is the matrix a:\n" << a << std::endl;
a = a.transpose(); // !!! do NOT do this !!!
std::cout << "and the result of the aliasing effect:\n" << a << std::endl;
}矩陣* 矩陣和矩陣* 向量操作
#include <iostream>
#include <Eigen/Dense>
using namespace Eigen;
int main()
{
Matrix2d mat; mat << 1, 2, 3, 4;
Vector2d u(-1,1), v(2,0);
std::cout << "Here is mat*mat:\n" << mat*mat << std::endl;
std::cout << "Here is mat*u:\n" << mat*u << std::endl;
std::cout << "Here is u^T*mat:\n" << u.transpose()*mat << std::endl;
std::cout << "Here is u^T*v:\n" << u.transpose()*v << std::endl;
std::cout << "Here is u*v^T:\n" << u*v.transpose() << std::endl;
std::cout << "Let's multiply mat by itself" << std::endl;
mat = mat*mat; std::cout << "Now mat is mat:\n" << mat << std::endl;
}點乘和叉乘
對於點積和叉乘積,需要使用dot()和cross()方法。
#include <iostream>
#include <Eigen/Dense>
using namespace Eigen;
using namespace std;
int main()
{
Vector3d v(1,2,3);
Vector3d w(0,1,2);
cout << "Dot product: " << v.dot(w) << endl;
double dp = v.adjoint()*w; // automatic conversion of the inner product to a scalar
cout << "Dot product via a matrix product: " << dp << endl;
cout << "Cross product:\n" << v.cross(w) << endl;
}#include <iostream>
#include <Eigen/Dense>
using namespace std;
int main()
{
Eigen::Matrix2d mat;
mat << 1, 2, 3, 4;
cout << "Here is mat.sum(): " << mat.sum() << endl;
cout << "Here is mat.prod(): " << mat.prod() << endl;
cout << "Here is mat.mean(): " << mat.mean() << endl;
cout << "Here is mat.minCoeff(): " << mat.minCoeff() << endl;
cout << "Here is mat.maxCoeff(): " << mat.maxCoeff() << endl;
cout << "Here is mat.trace(): " << mat.trace() << endl;
}陣列的運算(未完待續)
Eigen最小二乘估計
最小平方求解的最好方法是使用SVD分解。 Eigen提供一個作為JacobiSVD類,它的solve()是做最小二乘解。式子為Ax=b
經過和Matlab對比。
#include <iostream>
#include <Eigen/Dense>
using namespace std;
using namespace Eigen;
int main()
{
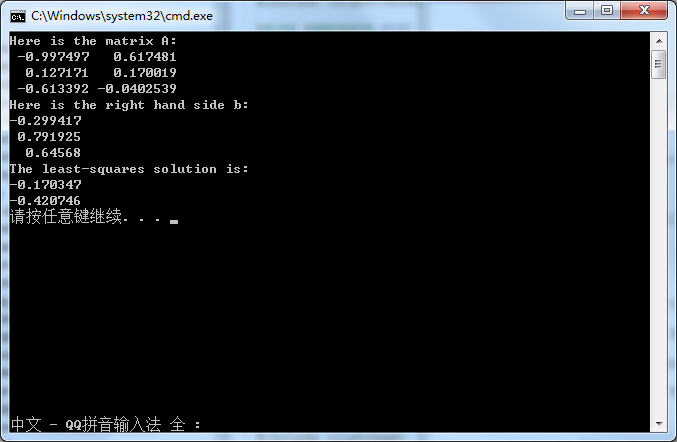
MatrixXf A = MatrixXf::Random(3, 2);
cout << "Here is the matrix A:\n" << A << endl;
VectorXf b = VectorXf::Random(3);
cout << "Here is the right hand side b:\n" << b << endl;
cout << "The least-squares solution is:\n" << A.jacobiSvd(ComputeThinU | ComputeThinV).solve(b) << endl;
}第二部分:
矩陣、向量初始化
#include <iostream>
#include "Eigen/Dense"
using namespace Eigen;
int main()
{
MatrixXf m1(3,4); //動態矩陣,建立3行4列。
MatrixXf m2(4,3); //4行3列,依此類推。
MatrixXf m3(3,3);
Vector3f v1; //若是靜態陣列,則不用指定行或者列
/* 初始化 */
Matrix3d m = Matrix3d::Random();
m1 = MatrixXf::Zero(3,4); //用0矩陣初始化,要指定行列數
m2 = MatrixXf::Zero(4,3);
m3 = MatrixXf::Identity(3,3); //用單位矩陣初始化
v1 = Vector3f::Zero(); //同理,若是靜態的,不用指定行列數
m1 << 1,0,0,1, //也可以以這種方式初始化
1,5,0,1,
0,0,9,1;
m2 << 1,0,0,
0,4,0,
0,0,7,
1,1,1;
//向量初始化,與矩陣類似
Vector3d v3(1,2,3);
VectorXf vx(30);
}C++陣列和矩陣轉換
使用Map函式,可以實現Eigen的矩陣和c++中的陣列直接轉換,語法如下:
//@param MatrixType 矩陣型別
//@param MapOptions 可選引數,指的是指標是否對齊,Aligned, or Unaligned. The default is Unaligned.
//@param StrideType 可選引數,步長
/*
Map<typename MatrixType,
int MapOptions,
typename StrideType>
*/
int i;
//陣列轉矩陣
double *aMat = new double[20];
for(i =0;i<20;i++)
{
aMat[i] = rand()%11;
}
//靜態矩陣,編譯時確定維數 Matrix<double,4,5>
Eigen:Map<Matrix<double,4,5> > staMat(aMat);
//輸出
for (int i = 0; i < staMat.size(); i++)
std::cout << *(staMat.data() + i) << " ";
std::cout << std::endl << std::endl;
//動態矩陣,執行時確定 MatrixXd
Map<MatrixXd> dymMat(aMat,4,5);
//輸出,應該和上面一致
for (int i = 0; i < dymMat.size(); i++)
std::cout << *(dymMat.data() + i) << " ";
std::cout << std::endl << std::endl;
//Matrix中的資料存在一維陣列中,預設是行優先的格式,即一行行的存
//data()返回Matrix中的指標
dymMat.data();矩陣基礎操作
eigen過載了基礎的+ - * / += -= = /= 可以表示標量和矩陣或者矩陣和矩陣
#include <iostream>
#include <Eigen/Dense>
using namespace Eigen;
int main()
{
//單個取值,單個賦值
double value00 = staMat(0,0);
double value10 = staMat(1,0);
staMat(0,0) = 100;
std::cout << value00 <<value10<<std::endl;
std::cout <<staMat<<std::endl<<std::endl;
//加減乘除示例 Matrix2d 等同於 Matrix<double,2,2>
Matrix2d a;
a << 1, 2,
3, 4;
MatrixXd b(2,2);
b << 2, 3,
1, 4;
Matrix2d c = a + b;
std::cout<< c<<std::endl<<std::endl;
c = a - b;
std::cout<<c<<std::endl<<std::endl;
c = a * 2;
std::cout<<c<<std::endl<<std::endl;
c = 2.5 * a;
std::cout<<c<<std::endl<<std::endl;
c = a / 2;
std::cout<<c<<std::endl<<std::endl;
c = a * b;
std::cout<<c<<std::endl<<std::endl;點積和叉積
#include <iostream>
#include <Eigen/Dense>
using namespace Eigen;
using namespace std;
int main()
{
//點積、叉積(針對向量的)
Vector3d v(1,2,3);
Vector3d w(0,1,2);
std::cout<<v.dot(w)<<std::endl<<std::endl;
std::cout<<w.cross(v)<<std::endl<<std::endl;
}
*/轉置、伴隨、行列式、逆矩陣
小矩陣(4 * 4及以下)eigen會自動優化,預設採用LU分解,效率不高
#include <iostream>
#include <Eigen/Dense>
using namespace std;
using namespace Eigen;
int main()
{
Matrix2d c;
c << 1, 2,
3, 4;
//轉置、伴隨
std::cout<<c<<std::endl<<std::endl;
std::cout<<"轉置\n"<<c.transpose()<<std::endl<<std::endl;
std::cout<<"伴隨\n"<<c.adjoint()<<std::endl<<std::endl;
//逆矩陣、行列式
std::cout << "行列式: " << c.determinant() << std::endl;
std::cout << "逆矩陣\n" << c.inverse() << std::endl;
}計算特徵值和特徵向量
#include <iostream>
#include <Eigen/Dense>
using namespace std;
using namespace Eigen;
int main()
{
//特徵向量、特徵值
std::cout << "Here is the matrix A:\n" << a << std::endl;
SelfAdjointEigenSolver<Matrix2d> eigensolver(a);
if (eigensolver.info() != Success) abort();
std::cout << "特徵值:\n" << eigensolver.eigenvalues() << std::endl;
std::cout << "Here's a matrix whose columns are eigenvectors of A \n"
<< "corresponding to these eigenvalues:\n"
<< eigensolver.eigenvectors() << std::endl;
}解線性方程
#include <iostream>
#include <Eigen/Dense>
using namespace std;
using namespace Eigen;
int main()
{
//線性方程求解 Ax =B;
Matrix4d A;
A << 2,-1,-1,1,
1,1,-2,1,
4,-6,2,-2,
3,6,-9,7;
Vector4d B(2,4,4,9);
Vector4d x = A.colPivHouseholderQr().solve(B);
Vector4d x2 = A.llt().solve(B);
Vector4d x3 = A.ldlt().solve(B);
std::cout << "The solution is:\n" << x <<"\n\n"<<x2<<"\n\n"<<x3 <<std::endl;
}除了colPivHouseholderQr、LLT、LDLT,還有以下的函式可以求解線性方程組,請注意精度和速度: 解小矩陣(4*4)基本沒有速度差別
最小二乘求解
最小二乘求解有兩種方式,jacobiSvd或者colPivHouseholderQr,4*4以下的小矩陣速度沒有區別,jacobiSvd可能更快,大矩陣最好用colPivHouseholderQr
#include <iostream>
#include <Eigen/Dense>
using namespace std;
using namespace Eigen;
int main()
{
MatrixXf A1 = MatrixXf::Random(3, 2);
std::cout << "Here is the matrix A:\n" << A1 << std::endl;
VectorXf b1 = VectorXf::Random(3);
std::cout << "Here is the right hand side b:\n" << b1 << std::endl;
//jacobiSvd 方式:Slow (but fast for small matrices)
std::cout << "The least-squares solution is:\n"
<< A1.jacobiSvd(ComputeThinU | ComputeThinV).solve(b1) << std::endl;
//colPivHouseholderQr方法:fast
std::cout << "The least-squares solution is:\n"
<< A1.colPivHouseholderQr().solve(b1) << std::endl;
}稀疏矩陣
稀疏矩陣的標頭檔案包括:
#include
typedef Eigen::Triplet<double> T;
std::vector<T> tripletList;
triplets.reserve(estimation_of_entries); //estimation_of_entries是預估的條目
for(...)
{
tripletList.push_back(T(i,j,v_ij));//第 i,j個有值的位置的值
}
SparseMatrixType mat(rows,cols);
mat.setFromTriplets(tripletList.begin(), tripletList.end());
// mat is ready to go!2.直接將已知的非0值插入
SparseMatrix<double> mat(rows,cols);
mat.reserve(VectorXi::Constant(cols,6));
for(...)
{
// i,j 個非零值 v_ij != 0
mat.insert(i,j) = v_ij;
}
mat.makeCompressed(); // optional稀疏矩陣支援大部分一元和二元運算:
sm1.real() sm1.imag() -sm1 0.5*sm1
sm1+sm2 sm1-sm2 sm1.cwiseProduct(sm2)
二元運算中,稀疏矩陣和普通矩陣可以混合使用
//dm表示普通矩陣
dm2 = sm1 + dm1;
也支援計算轉置矩陣和伴隨矩陣
參考以下連結
第三部分:
其他相關部落格:
1、單獨下載與安裝:https://blog.csdn.net/augusdi/article/details/12907341
2、一篇較詳細的教程:https://blog.csdn.net/wzaltzap/article/details/79501856
3、計算特徵值特徵向量:https://blog.csdn.net/wokaowokaowokao12345/article/details/47375427