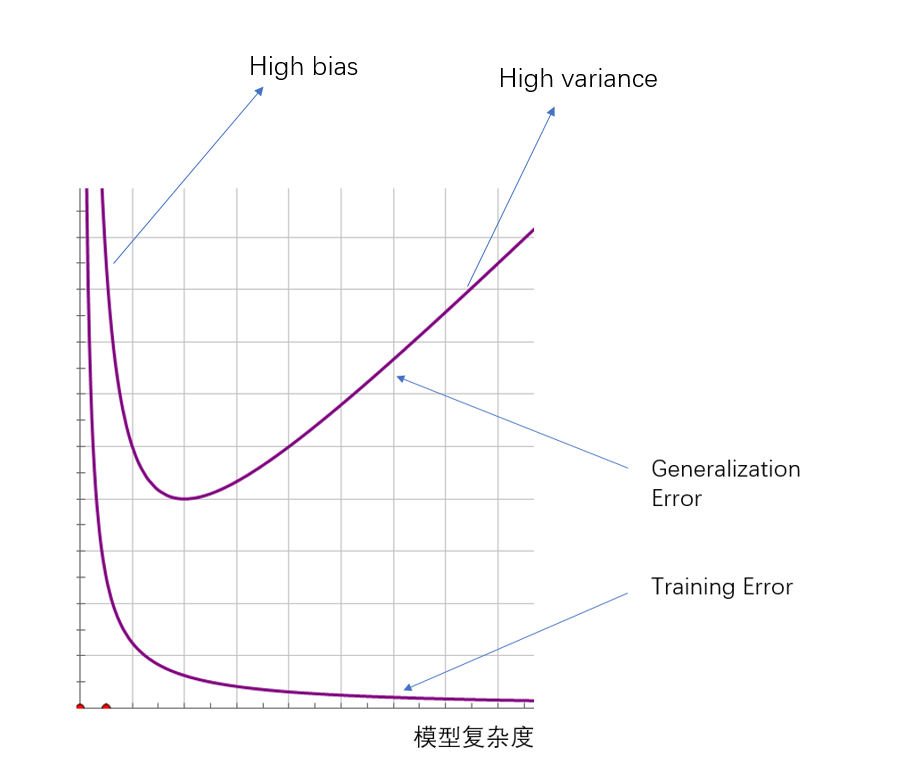
【機器學習筆記】權衡 bias 和 variance
Training error & Generalization error
Training error 是說對於一個假設
Generalization error 是指對於一個假設
當樣本數量
bias 和 variance
Generalization error可以用如下的式子表出(換種表示):
以迴歸模型為例,假設我們的一個預測模型,得出樣本資料的期望為
bias
bias 是模型過於簡單的時候,欠擬合, 模型表現出來的誤差:
為了計算方便(去掉絕對值),我們在計算時用
variance
是指模型過於複雜時,過擬合表現出的誤差;表現出來的一些特性僅僅適用於訓練集,而一旦應用於其他資料集(測試集)就會出現較大誤差
比如,我們用原來的訓練集
ϵ
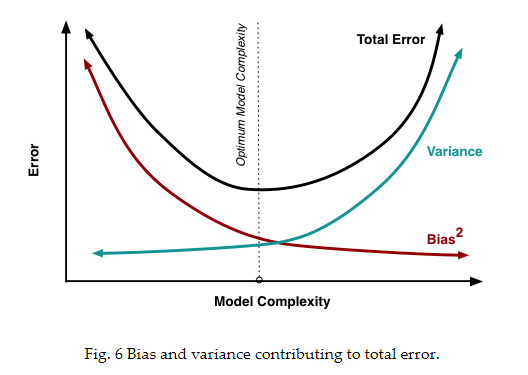
Generalization error 與 bias, variance的關係可以用下圖表示:
ERM(empirical risk minimization)
ERM(empirical risk minimization) 本質就是最小化經驗誤差
顯式表示為:
經驗誤差為:
也就是之前說的training error.
演算法的目的就是求得:
模型複雜度的影響:
我們先假定問題是PAC(probably approximately correct) 的(下一篇我會展開說明PAC,以及為什麼得到下面那個式子),也就是說,我們可以通過優化訓練誤差來近似估計泛化誤差,對於訓練過程中,訓練誤差最小的
其中
我們可以近似理解為:
和上圖類似,具體的影響如下圖的曲線所表示。