資料結構-陣列與壓縮矩陣
陣列的定義
陣列是由n(n>1)個具有相同資料型別的資料元素a1...an組成的有序序列,且該序列必須儲存在一塊地址連續的儲存單元中。
1.陣列中的陣列元素就有相同的資料型別
2.陣列是一種隨機存取結構,給定一組下標就可以訪問與其對應的資料元素。
3.陣列中的資料元素個數是固定的。
行向量的一位陣列形式

列向量的一位陣列形式

陣列的兩種順序儲存方式
1.行優先順序(Row Major Order):將陣列元素按行排列,第i+1個行向量緊接著第i個行向量後面。對於二維陣列,按行優先順序儲存的線性序列為:

c語言是按行優先順序儲存的。
2.列優先順序(Column Major Order)

設有二維陣列A=(aij)mxn ,若每個元素佔用的儲存單元數為 /(個),LOC[a11]表示元素a11的首地址(也可以用a00表示首地址),即陣列的首地址。
1.以“行優先順序”儲存
(1)第1行中的每個元素對應的(首)地址是:
![]()
注:如果下標從0開始:LOC[a1j] = LOC[a11]+j x /
(2)第2行中的每個元素對應的(首)地址是:
![]()
注:如果下標從0開始:LOC[a2j] = LOC[a11]+(1xn)x/ + jx/
(3)第m行中的每個元素對應的(首)地址是:

注:如果下標從0開始:LOC[amj] = LOC[a11]+(mxn)x/ + jx/
三維陣列中任一元素aijk的(首)地址是:
![]()
多維陣列推而廣之。
2.以“列優先順序”儲存
(1)第1列中的每個元素對應的(首)地址是:
![]()
(2)第2列中的每個元素對應的(首)地址是:

(3)第n列中的每個元素對應的(首)地址是:

特殊矩陣的壓縮儲存
特殊矩陣:是指非零元素或零元素的分佈有一定規律的矩陣
對於高階矩陣,若其中非零元素呈現某種規律分佈或者矩陣中有大量的零元素,若仍然用常規方法儲存,可能儲存重複的非零元素或零元素,將造成儲存空間的大量浪費。對這類矩陣進行壓縮儲存。
1.多個相同得非零元素只分配一個儲存空間
2.零元素不分配空間
比如:一個nxn的二階矩陣壓縮成一個n的一維空間,大大減少了儲存空間,即壓縮儲存。
1.對稱矩陣
若一個n階方陣A=(aij)nxn中的元素滿足aij=aji ,i>=1,j<=n 且i≠j,則稱A為對稱矩陣
即:關於對角線對稱

對稱矩陣中的元素關於主對角線對稱,因此,讓每一對對稱元素aij 和 aji(i≠j)分配一個儲存空間,則n^2個元素壓縮儲存到
n(n+1) /2 個儲存空間(即只儲存下三角的元素,包含對角線即1+2+3+...+n=n(n+1) /2),能節約近一半的儲存空間。
假設按“行優先順序”儲存下三角形(包括對角線)元素;設用一維陣列(向量)sa[0....n(n+1)/2]儲存n階對稱矩陣。為了便於訪問,必須找出矩陣A中的元素下標值(i,j)和向量sa[k]的下標值k之間的對應關係。

若i>=j:aij 在下三角形中,直接儲存在sa中。aij之前的i-1行共有元素個數:1+2+....+(i-1) = i(i-1)/2,在第i行上,aij之前恰有j-1個元素,因此,元素aij儲存在向量sa中時的下標值k之間的對應關係是:
k=i x (i-1) /2 + j-1 (i>=j)
若i<j: 則aij是在上三角矩陣中。因為aij=aji,在向量sa中儲存的是aji,即:
k=j x (j-1) /2 + i-1 (i<j)
所以,對稱矩陣元素aij儲存在向量sa中時的下標值k與(i,j)之間的對應關係是:

注意:此處i,j的下標均是從1開始的
如果下標從0開始則關係式:
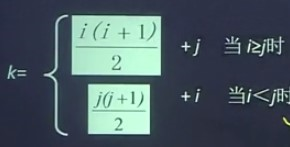
2.三角矩陣
(1)以主對角線劃分,三角矩陣有上三角和下三角兩種。
(2)上三角矩陣的下三角(不包括主對角線)中的元素均為常數c(一般為0),下三角矩陣正好相反,它的主對角線上方均為常數。

三角矩陣中的重複元素c可共享一個儲存空間,其餘元素正好有n(n+1) /2個,因此三角矩陣可壓縮儲存到向量sa[0...n(n+1) /2]中(一位陣列),其中c存放在向量的最後1個分量重。
上三角矩陣元素aij儲存在向量sa中時的下標k與(i,j)之間的對應關係是:
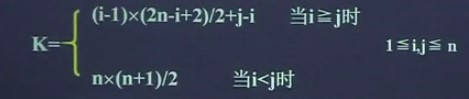
下三角矩陣元素aij儲存在向量sa中時的下標值k與(i,j)之間的對應關係是:
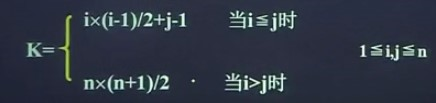
3.對角矩陣
矩陣中,除了主對角線和主對角線上或下方若干條對角線上的元素以外,其餘元素皆為零。即所有的非零元素集中在以對角線為中心的帶狀區域中。

特點:以對角線為中心,第一行和最後一行都只有2個元素,其餘每行都有三個元素,所以一個n行的對角矩陣中總數=3(n-2)+4 = 3n-2
對角矩陣可按行優先順序或對角線順序,將其壓縮儲存到一個向量中,並且也能找到每個非零元素和向量下標的對應關係,仍然以三對角矩陣為例討論:當i=1,j=1、2, 當i=n,j=n-1、n,當1<i<n-1,j=i-1、i、i+1,其餘元素都為0;
對這種矩陣,當以按“行優先順序”儲存時,第1行和第n行是2個非零元素,其餘每行的非零元素都是3個,則需儲存的元素個數為3n-2個。
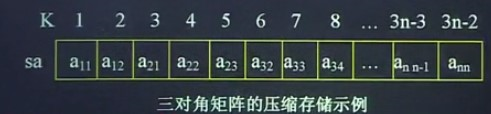
陣列sa(sa從1開始)中的元素sa[k]與三對角矩陣中的元素aij (i,j從1開始)存在一一對應關係,在aij之前有i-1行,共有3x(i-1)-1個非零元素,在第i行,有j-i+1個非零元素(因為j-1=-1、0、1,所以j-i+1=0、1、2,即按這種位置順序儲存即可),這樣,非零元素aij的地址位:
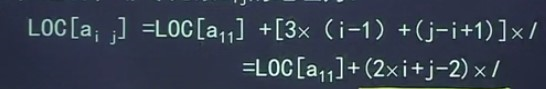
上例中,a34對應著sa[8],k=2xi+j-2=2x3+4-2=8
稱sa[0....3n-2]是n階三對角矩陣A的壓縮儲存。
稀疏矩陣
稀疏矩陣(Sparse Matrix):設矩陣A是一個nxm的矩陣中有s個非零元素,設 δ = s /(nxm),稱矩陣δ為稀疏因子,如果某一矩陣的稀疏因子δ滿足δ<=0.05時稱為稀疏矩陣。

稀疏矩陣的壓縮儲存
對於稀疏矩陣,採用壓縮儲存方法時,只儲存非0元素。須儲存非0元素的行下標值、列下標值、元素值。
一個三元組(i,j,aij)唯一確定稀疏矩陣的一個非零元素。
1.三元組順序表
若以行序為主序,稀疏矩陣中所有非0元素的三元組,就可以構成該稀疏矩陣的一個三元組順序表。
相應的資料結構定義如下:
(1)三元組結點定義
元素節點

(2)三元組順序表定義
資訊總覽結構

2.十字連結串列
對於稀疏矩陣,當非0元素的個數和位置在操作過程中變化較大時,採用鏈式儲存結構表示比三元組的線性表更方便,矩陣中非0元素的結點所含的域有:行、列、值、行指標(指向同一行的下一個非0元)、列指標(指向同一列的下一個非0元)。其次,十字交叉連結串列還有一個頭節點,結點結構如圖所示。


結構定義

由定義知,稀疏矩陣中同一行的非0元素由right指標域連結成一個行連結串列,由down指標域連結成一個列連結串列。則每個非0元素既是某個行連結串列中的一個結點,同時又是某個列連結串列中的一個結點,所有非0元素構成一個十字交叉的連結串列。稱為十字連結串列。
此外,還可用兩個一維陣列分別儲存行連結串列的頭指標和列連結串列的頭指標。
優勢:查詢方便,缺點:複雜
廣義表
廣義表是線性表的推廣和擴充,在人工智慧領域中應用十分廣泛。把線性表定義為n(n>=0)個元素a1,a2,....an的又窮序列,該序列中的所有元素具有相同得資料型別且只能是原子項。
所謂原子項可以是一個數或一個結構,是指結構上不可再分的。若放鬆對元素的這種限制,或許它們有其自身結構,就產生了廣義表的概念。
廣義表(Lists,又稱為列表):是由n(n>=0)個元素組成的有窮序列:LS=(a1,a2,....an);其中ai 或者是原子項,或者是一個廣義表。LS是廣義表的名字,n為它的長度。若ai 是廣義表,則稱為LS的子表。習慣上:原子用小寫字母,子表用大寫字母。
定義非空廣義表LS:
(1).a1(表中第一個元素)稱為表頭;
(2).其餘元素組成的子表稱為表尾;(a2,a3,a4....an)
(3).廣義表中所包含的元素(包括原子和子表)的個數稱為表的長度
(4).廣義表中括號的最大層數稱為表深(度)
(5).兩個基本操作GetHead() :取表頭元素;GetTail():取表尾

