遞迴演算法實現斐波那契數列
阿新 • • 發佈:2018-12-31
假定兔子在出生兩個月後,就有繁殖能力,一對兔子每個月能生出一對小兔子來。如果所有兔子都不死,那麼一年以後可以繁殖多少對兔子?
這就是著名的斐波那契數列,也稱作兔子數列。
一、問題分析
剛開始,有1對幼兔,兔子總對數為1;
經過一個月後,幼兔長為小兔,兔子總對數為1;
經過二個月後,幼兔長大為成年兔子,並生出1對幼兔,兔子總對數為2對;
經過三個月後,成年兔子兔子再生出1對幼兔,幼兔長大為小兔,兔子總對數達到3對;
-------------------------------------------
依次類推可以得到下表:
|
月份 |
0 | 1 | 2 | 3 | 4 | 5 | 6 | ... |
| 幼兔對數 |
1 |
0 | 1 | 1 | 2 | 3 | 5 | ... |
| 小兔對數 | 0 | 1 | 0 | 1 | 1 | 2 | 3 | ... |
| 成兔對數 | 0 | 0 | 1 | 1 | 2 | 3 | 5 | ... |
| 總對數 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | ... |
根據上表可以發現,對於兔子總對數,從第三項開始,每一項均為前兩項之和。
二、斐波那契數列
在數學上,斐波納契數列以如下被以遞推的方法定義:F(1)=1,F(2)=1, F(n)=F(n-1)+F(n-2)(n>=3,n∈N*),
下面讓我們通過遞迴演算法來求解這個兔子數列吧。
三、不同演算法實現
package com.liao.algorithm; import java.util.Scanner; public class Recursion { private static int a;//輸入月份數 static int t1, t2, t3;//統計程式碼執行次數 public static void main(String[] args) { while (a <= 0) { System.out.println("請輸入經過月份(1~n):"); a = new Scanner(System.in).nextInt(); } System.out.println(a + "個月後,兔子總數為:" + fib1(a) + ",執行次數:" + t1); System.out.println(a + "個月後,兔子總數為:" + fib2(1, 1, a) + ",執行次數:" + t2); System.out.println(a + "個月後,兔子總數為:" + fib3(1, 1, a) + ",執行次數:" + t3); } // 遞迴實現 public static int fib1(int n) { t1++; if (n < 3) return 1; return fib1(n - 1) + fib1(n - 2); } // 尾遞迴實現 public static int fib2(int fir, int sen, int n) { t2++; if (n < 3) return 1; if (n == 3) return fir + sen; return fib2(sen, fir + sen, n - 1); } // 迭代實現 public static int fib3(int fir, int sen, int n) { int total = 1; if (n < 3) return total; while (n > 2) { t3++; total = fir + sen; fir = sen; sen = total; n--; } return total; } }
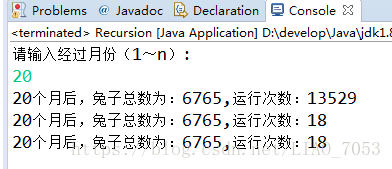
四、執行結果
五、分析小結
1、三種演算法都得到了一樣的結果,但是有一個地方有非常大的區別,那就是程式碼執行次數上,或者說是空間複雜度。
2、遞迴演算法即第一種方法,程式碼看著最簡潔,但其重複運算次數太多,運算效率低,其時間複雜度為O(2^n),空間複雜度為O(n);
3、尾遞迴演算法將每一次的計算結果作為引數傳入方法,減少不必要的重複運算,運算效率大幅提高,時間複雜度為O(n);
4、迭代演算法即第三種演算法,是通過我們常用的迴圈判斷語句實現,由於僅建立了 4個基礎變數,通過賦值傳遞數值,時間複雜度(O(n))和空間複雜度(O(1))均是最低的。