演算法工程師修仙之路:吳恩達機器學習(十四)
吳恩達機器學習筆記及作業程式碼實現中文版
第十章 支援向量機
直觀上對大間隔的理解
-
人們有時將支援向量機看作是大間距分類器。
-
支援向量機模型的代價函式,在左邊這裡我畫出了關於 z 的代價函式 ,此函式用於正樣本,而在右邊這裡我畫出了關於 z 的代價函式 ,橫軸表示 z。

-
最小化代價函式的必要條件
- 如果你有一個正樣本, ,則只有在z >= 1時,代價函式 才等於0。換句話說,如果你有一個正樣本,我們會希望 ,反之,如果 ,函式 ,它只有在z <= -1的區間裡函式值為 0。
- 事實上,如果你有一個正樣本 ,則其實我們僅僅要求 大於等於 0,就能將該樣本恰當分出,這是因為如果 的話,我們的模型代價函式值為0,類似地,如果你有一個負樣本,則僅需要 就會將負例正確分離。
- 但是,支援向量機的要求更高,不僅僅要能正確分開輸入的樣本,即不僅僅要求 ,我們需要的是比0值大很多,比如大於等於1,或者比0小很多,比如我希望它小於等於-1,這就相當於在支援向量機中嵌入了一個額外的安全因子,或者說安全的間距因子。
-
如果 非常大,則最小化代價函式的時候,我們將會很希望找到一個使第一項為 0 的最優解。因此,讓我們嘗試在代價項的第一項為 0 的情形下理解該優化問題。
- 首先支援向量機的代價函式表示如下: 。
- 我們已經看到輸入一個訓練樣本標籤為 ,你想令第一項為 0,你需要做的是找到一個 ,使得 ,類似地,對於一個訓練樣本,標籤為 ,為了使 函式的值為0,我們需要 。
- 因為我們將選擇引數使第一項為0,因此這個函式的第一項為0,因此是 乘以 0 加上二分之一乘以第二項。這將遵從以下的約束: ,如果 是等於 1 的, ,如果樣本 是一個負樣本。
-
具體而言,如果你考察下面這樣一個數據集,其中有正樣本,也有負樣本,可以看到這個資料集是線性可分的。
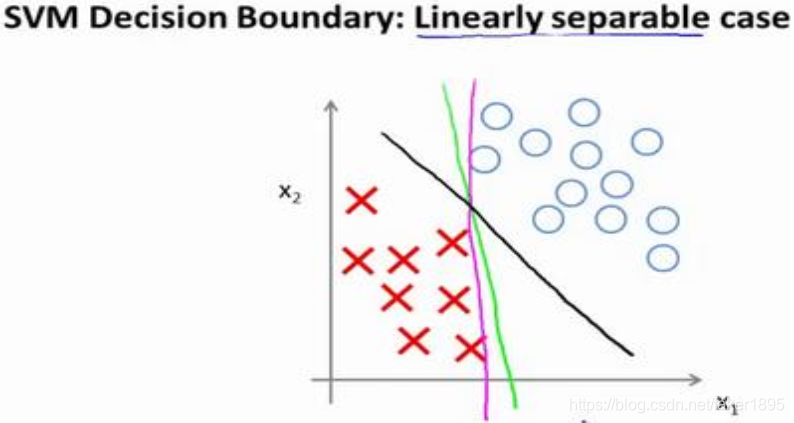
-
支援向量機將會選擇這個黑色的決策邊界,黑線看起來是更穩健的決策界。在分離正樣本和負樣本上它顯得的更好。數學上來講,這條黑線有更大的距離,這個距離叫做間距(margin)。
-
當畫出兩條額外的藍線,我們看到黑色的決策界和訓練樣本之間有更大的最短距離。然而粉線和藍線離訓練樣本就非常近,在分離樣本的時候就會比黑線表現差。因此,這個距離叫做支援向量機的間距,而這是支援向量機具有魯棒性的原因,因為它努力用一個最大間距來分離樣本,因此支援向量機有時被稱為大間距分類器。
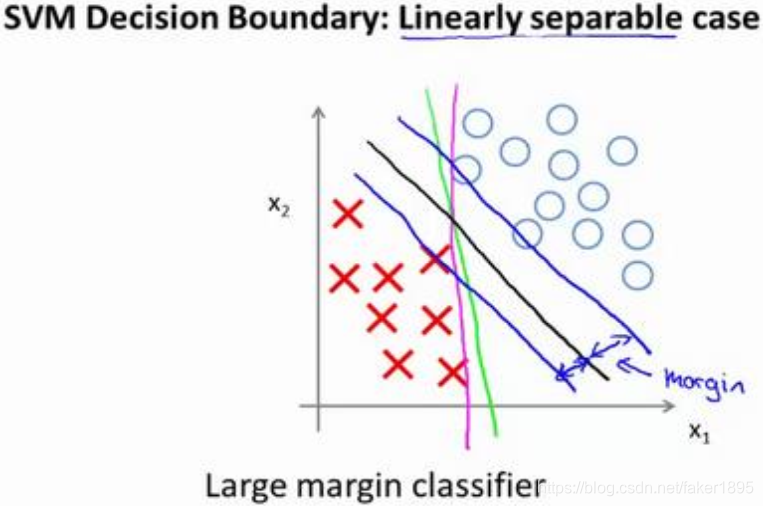
-
我們將這個大間距分類器中的正則化因子常數 設定的非常大,因此對這樣的一個數據集,也許我們將選擇黑線這樣的決策界,從而最大間距地分離開正樣本和負樣本。
-
在讓代價函式最小化的過程中,我們希望找出在 和 兩種情況下都使得代價函式中左邊的這一項儘量為零的引數。如果我們找到了這樣的引數,則我們的最小化問題便轉變成:
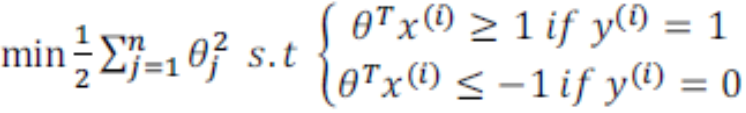
-
事實上,支援向量機現在要比這個大間距分類器所體現得更成熟,尤其是當你使用大間距分類器的時候,你的學習演算法會受異常點(outlier)的影響。
- 比如我們加入一個額外的正樣本:
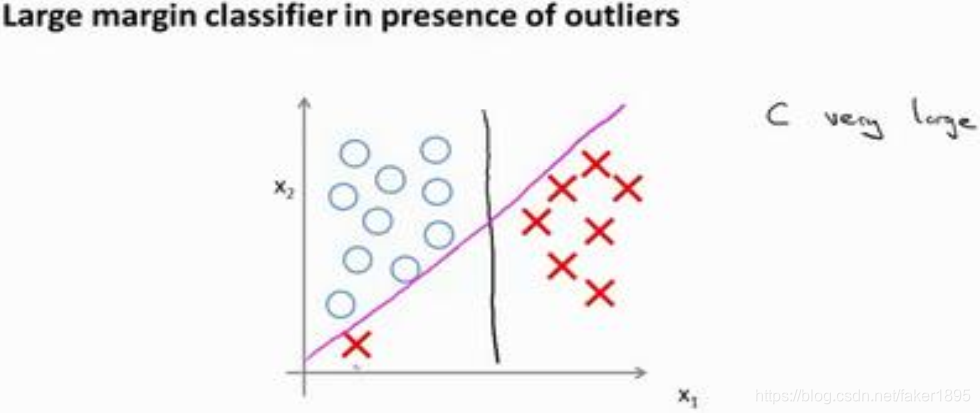
- 在這裡,如果你加了這個樣本,為了將樣本用最大間距分開,也許我最終會得到一條類似這樣粉色的線的決策界,僅僅基於一個異常值,僅僅基於一個樣本,就將我的決策界從這條黑線變到這條粉線,這實在是不明智的。
- 而如果正則化引數 設定的非常大,這事實上正是支援向量機將會做的。它將決策界,從黑線變到了粉線,但是如果 設定的小一點, 如果你將 設定的不要太大,則你最終會得到這條黑線。
- 當然資料如果不是線性可分的,如果你在這裡有一些正樣本或者你在這裡有一些負樣本,則支援向量機也會將它們恰當分開。因此,大間距分類器的描述,僅僅是從直觀上給出了正則化引數 非常大的情形。
- 的作用類似於 , 是我們之前使用過的正則化引數。這只是 非常大的情形,或者等價 非常小的情形。你最終會得到類似粉線這樣的決策界,但是實際上應用支援向量機的時候,當 不是非常非常大的時候,它可以忽略掉一些異常點的影響,得到更好的決策界。甚至當你的資料不是線性可分的時候,支援向量機也可以給出好的結果。
- 比如我們加入一個額外的正樣本:
-
較大時,相當於 較小,可能會導致過擬合,高方差; 較小時,相當於 較大,可能會導致低擬合,高偏差。
