凸函式與簡森不等式(Jensen's inequality)
阿新 • • 發佈:2019-01-01
0. 凸函式常見舉例
- 負對數函式:
−lnx xlnx (二階導數為1x ,恆為整數,因為定義域的關係)
1. 凸函式的判斷準則
定義:
f(λx+(1−λ)x2)≤λf(x)+(1−λ)f(y) - 甚至可以找一些特例,
f(x2+y2),f(x)2+f(y)2
- 甚至可以找一些特例,
二次求導
- 大於 0,比如
f(x)=xlogx,f′′=1x ,凸的; - 小於 0,比如
f(x)=ax−xlogx,f′′=−1x ,凹的;
- 大於 0,比如
2. convex function (凸函式)
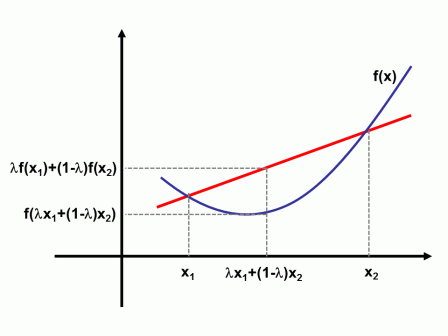
弦在弧上(也是大名鼎鼎的Jensen’s inequality),也即如上圖所示:
也可理解為函式(凸函式)的期望大或等於期望的函式。
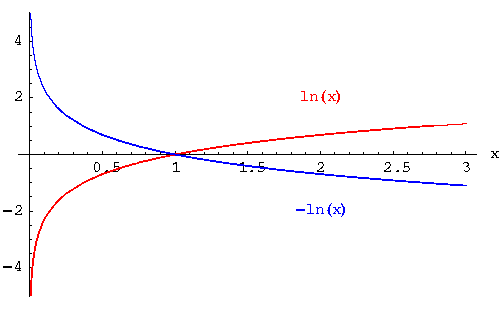
f(x)=lnx,f′′=−1x2 :f(x)=−lnx,f′′=1x2
3. effective domain & proper convex function
effective domain
給定一個向量空間
X ,一個對映到拓展實數(R∪{±∞} )的凸函式定義為,f:X→R∪{±∞} ,該函式的 effective domain 被定義為:domf={x∈X|f(x)<+∞} proper convex function
一個凸函式是 proper 的,如果滿足它的effective domain 不為空,且其值永遠大於
−∞ 也即下述兩點:
f(x)<+∞ ,至少一個x (effective domain 不為空)f(x)>−∞ ,∀x ;
4. 從凸函式到簡森不等式
- convex function,凸函式;concave function,凹函式;
如果
比如隨機變數,
這裡的
兩獨立的隨機變數
