【宣告：鄙人菜鳥一枚，寫的都是初級部落格，如遇大神路過鄙地，請多賜教；內容有誤，請批評指教，如有雷同，屬我偷懶轉運的，能給你帶來收穫就是我的部落格價值所在。】
   今天一位同事跟我談起Hadoop，剛好這期部落格我也正準備寫點這方面相關的綜述，就跟他聊了聊。談起Hadoop不得不談及MapReduce，它是基於Hadoop分散式大資料處理平臺的一個非常重要的計算框架，通俗些講：MapReduce就像是一種套路，按著這種套路來解決普通計算模式難以接受的量級資料運算，分步分解、各個擊破。我不知道這樣說算不算通俗精準，但就是這個意思。這裡我也不打算就Hadoop和MapReduce做全面且詳細的概述，畢竟不是一兩句話就能講清楚的，所以預設觀眾姥爺們有這些基礎知識，沒有的話也沒關係，這次談的是基於MapReduce的大圖劃分的一些常用演算法，講的很基礎，中間會有一段專門解釋MapReduce。下面移步正文（可能在格式上有些正式了，希望別反感）：

1 背景及意義

  在今天這個資訊化社會中，隨著網際網路使用者的急劇增加，越來越多的網路資料問題擺在了我們面前。而在大資料時代下，大規模圖資料處理問題便是一大熱點。類似於網狀圖，如果將每個網路使用者看作圖中的節點，而將使用者與使用者之間的關係看作圖中的邊，那麼整個網路就可看作一張網路圖，大量的網路圖組成的集合便是圖資料。隨著網路使用者規模的不斷擴大，與之對應的網路圖結構愈加複雜，甚至有數十億個節點和上萬億條邊，普通的單臺計算機由於運算記憶體的限制，無法承載這種巨大的處理任務，這給資料處理中常見的圖計算（如獲取連通分量和PageRank）帶來了巨大的挑戰。
  解決單機能力的侷限性問題，最好的方法就是利用分散式計算，即將大規模圖資料劃分成多個子圖裝載到分割槽中，利用大型的分散式系統進行處理。為了提高不同分割槽間的並行處理速度，需要保持這些子圖的規模均衡，同時減少通訊開銷，所以連線不同分割槽的邊數應當足夠小。所以，基於MapReduce的大規模圖資料劃分演算法研究對解決圖論計算問題具有極大的意義。
  本文將綜合前人的研究，介紹圖劃分演算法的研究現狀，分析、比較它們的效能特點，以及詳細闡述基於MapReduce的分散式圖劃分演算法，從而使讀者能系統而全面地瞭解圖劃分與分散式圖劃分演算法。

2 圖資料劃分的研究現狀

  圖資料劃分問題是經典的NP（Non-deterministic Polynomial）完全問題，通常很難在有限的時間內找到圖劃分的最優解[1]。儘管其是難解問題，從20 世紀90 年代初期至今，國內外研究者不斷對圖劃分及其相關問題進行深入研究，提出了許多效能較好的圖劃分演算法。現主要有譜方法、幾何方法、啟發式方法、智慧優化演算法、多層劃分演算法等。[2]

2.1 譜方法

  1990 年，R. Leland 和B. Hendrickson 提出了譜方法。譜方法主要是針對圖的二劃分而言的。它的基本思想是用圖矩陣的第二大特徵值和特徵向量來實現圖的劃分。譜方法能為許多不同類的問題提供較好的劃分，但是譜方法的計算量非常大。H. Simon 和S. Barnard 於1993 年對譜方法進行了改進，具體是用多層的譜二分(MSB) 有效地減少了演算法求解特徵向量的執行時間。

2.2 幾何方法

  幾何方法根據給定圖的幾何資訊來尋找較好的劃分。幾何方法主要包括座標巢狀二分法、遞迴慣性二分法、空間填充曲線方法。1987 年，S. Bokari 和M. Berger 提出了座標巢狀二分法。其思想是：先選擇網格在平面座標上具有最長長度的一維，接著沿著選中那一維的方向對網格進行劃分。該方法是一種遞迴二分法，其演算法有很快的執行速度，但其缺點是劃分質量非常低，而且還會產生不連通的子區域。為解決上述缺點，M. Heath 和P. Raghavan 於1995 年對其進行了改進，然而只能沿著兩座標軸垂直或者平行方向劃分。遞迴慣性二分法是在座標巢狀二分法的基礎上提出來的，其不再用平面座標軸，而是用慣性主軸，從而降低了不連通子區域的數量；但是遞迴慣性二分法在劃分時還是僅能按照座標軸的某一維進行。1994 年，S. Ranka 和C. Ou 提出了空間填充曲線方法，該方法是一種基於多維的劃分方法。其首先對多維曲線上的資料單元進行排序，這主要是依據網格的質心來實現排序。然後根據排序的結果進行圖的劃分。

2.3 啟發式方法

  W. Kernighan 和S. Lin 提出了KL 演算法，它是一種比較典型的基於啟發式規則的求解策略。它的主要思想是先將圖隨機化成兩等分，然後對交換任意兩個頂點能導致的收益值進行估價，再高效地從中選擇收益最高的點進行交換。該演算法通常處理一萬個頂點以內的圖。 M. Fiduccia 和M. Mattheyses 提出的FM 演算法對KL 演算法進行了改進。FM 演算法採用單點移動，並引入了桶列表資料結構，減少了時間複雜度。該類方法不需要知道節點的座標資訊，而是需要根據節點之間的連線資訊進行劃分。2000 年，S. Dutt 和W. Deng 從頂點的移動次數對FM 演算法進行改進。2002 年，S. Dutt 和W. Deng 又從收益的計算方式進行改進。

2.4 智慧優化演算法

  因智慧優化演算法模擬自然界已知的進化方法而具有一定的優越性，一直備受來自各個領域研究者的關注。近年來智慧優化演算法被廣泛用來解決圖劃分問題。2007年，P. Chardaire 等人[3]提出了一種基於種群的元啟發式演算法PROBE (population reinforced optimization based exploration)。PROBE 演算法有些類似於遺傳演算法，但該演算法沒有選擇、突變和置換的概念，因而比遺傳演算法方法要簡單。

2.5 多層劃分演算法

  為了處理規模較大的圖，文獻[4]提出了多層的圖劃分框架METIS。多層劃分演算法包括3 個階段：粗糙化 (coarsening) 階段、初始劃分、反粗糙化階段(uncoarsening)。第一階段通過粗糙化 (coarsening) 技術將大圖約化為可接受的小圖；第二階段將第一階段獲得的小圖進行隨機劃分，並進行優化；第三階段通過反粗糙化 (uncoarsening) 技術以及優化技術將小圖的劃分還原為原圖的劃分。該演算法廣泛地應用在各類大圖的劃分，對於百萬規模以內的圖，通常具有較好的實際效果。

2.6 小結

  圖劃分問題普遍存在較高的計算複雜度，但圖資料在現實中具有重要的價值，這也是人們不斷追求更簡易的圖劃分演算法的原因。上文提到的五種圖劃分演算法在處理方法與結構上各具特色，也各有優劣，但就所能處理的圖資料規模上來講，分成集中式圖劃分演算法與分散式圖劃分演算法。
集中式圖劃分演算法 可以處理節點數和邊數較少的圖，包括區域性改進圖劃分演算法和全域性圖劃分演算法，其中區域性改進圖劃分演算法中比較經典的是KL演算法[5]和FM演算法[6]，全域性圖劃分演算法中比較經典的是Laplace圖特徵值譜二分法[7]和多層圖劃分演算法[8]。這些演算法具有較高的時問複雜度，無法處理節點數為百萬級以上的圖，因此這些演算法不適用於大資料時代中大規模的圖處理。
分散式圖劃分演算法  是針對近些年出現的大規模網路圖而研究出來的，分為靜態圖劃分演算法和動態圖劃分演算法，其中靜態圖劃分演算法的工作比較多，主要包括BHP演算法[9]、靜態Mizan演算法[10]、BLP演算法[11]等；動態圖划算法經典的主要包括動態Mizan演算法[12]和xDGP演算法[13]等。
  相比集中式圖劃分演算法，分散式的圖演算法在大資料時代具有無法比擬的優勢，所以本文接下來詳細介紹基於MapReduce的分散式圖劃分演算法。

3 基於MapReduce的分散式圖劃分演算法

3.1 MapReduce模型

  MapReduce 是一種程式設計模型，用於大規模資料集（大於1TB）的並行運算。在大規模資料集的處理與計算方面有著極大的優勢，且作為開源應用平臺，MapReduce已被廣泛應用於Hadoop、Phoenix、Mars、Cell MapReduce、FPMR、Ussop。[14] MapReduce 適合具有大量相同的基本計算的資訊處理場合（例如，web 圖中的節點），MapReduce 思想來源於高階函數語言程式設計，提供了一個抽象定義的Mapper（對映函式，指定每個record的計算）和Reducer（歸約函式，指定map輸出結果的整合），Mapper把一組鍵值對對映成一組新的鍵值對（作為處理基元），指定併發的Reducer對生成的鍵值對進行並行操作。這兩個階段的處理結構如圖 1 所示。
  根據 MapReduce 程式設計模型，開發人員只需提供對應的Mapper和Reducer實現程式碼。在分散式檔案系統（DFS）上，執行狀態（runtime）負責建立分散式叢集上程式執行的環境。除此外，它可以實現排程（資料移動程式碼）、處理故障和大型分散式排序和洗牌操作之間的對映問題。
作為一種優化，MapReduce 支援combiner（組合器）的使用，與Reducer機制類似，只是他們可以直接作用於Mapper的輸出，故而可以將它看作mini-Reducer。Combiner執行在叢集中每個節點之間，但不能使用其他節點的分立結果。鑑於中間鍵值對最終必須通過網路Shuffle與Sort匹配到合適的Reducer，combiner允許程式設計師歸約部分結果，從而減少了網路流量。

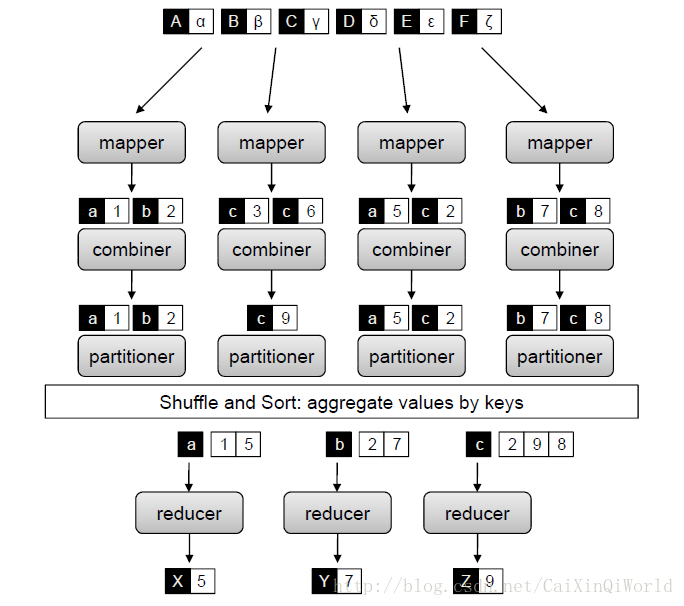
        圖 1︰ MapReduce模型的map與reduce階段的處理結構示意圖。

  MapReduce的一個重要部分便是partitioner（劃分），它負責劃分中間鍵域和為Reducer分配中間鍵值對。預設的partitioner會計算Reducer數目模數的雜湊值。Partitioner在合適的雜湊函式的幫助下可大致將中間鍵域劃分均勻，但這不能保證良好的負載平衡，因為可能出現高度偏態分佈也具有相同的關聯鍵值。

3.2 MapReduce圖劃分演算法

  定義一個標準的向量圖 G=(V,E)，其中組成的節點 V和向量邊 E，且 N+(vi)=vj│(vi,vj)∈E 和 N−(vi)=vj│(vj,vi)∈E 是所有相鄰節點vi組成的集合，圖劃分就是給定合適的向量圖G，將節點集V劃分為互不相交的k個子集 V1,V2,…,Vk。標量圖還預設支援用兩個互動向量邊替換每個標量邊，節點和邊上可能附加有額外的元資料。舉個簡單的例子，社會網路（其中節點代表人）可能有附加到邊和節點上的屬性資訊（如指示屬性的朋友或配偶關係）及統計資訊（如年齡、性別、住址）。圖劃分方法需要滿足兩個主要原則：一是子圖與子圖之間相連的邊儘量少，即互動邊數小；二是子圖與子圖的規模應當差不多，即負載均衡。
  基於以上的圖劃分定義及劃分演算法滿足的原則，這裡介紹一大類作用在稀疏向量圖上的迭代圖演算法，其中每次迭代過程如下︰
1. 計算每個節點（作為函式）的內部狀態和區域性圖結構；
2. 將各部分結果（以任意訊息形式存在）通過向量邊傳遞給每個節點的相鄰節點；
3. 基於傳入的部分結果，計算每個節點並同時改變節點的內部狀態。
  通常情況下，這種演算法需迭代一定次數，且每一次迭代過程均要使用迭代圖上一次的歷史狀態作為下 一次迭代的輸入，直到滿足迭代終止條件。運用以上圖演算法的一個經典例子就是 PageRank，它是基於拓撲結構的知名演算法，用來計算節點（Page ID）在圖中的重要性。對於圖中每個節點，PageRank 計算 P(vi) （即：圖中節點vi的概率），一個節點的概率主要取決於圖的拓撲結構，但計算上還會考慮阻尼因子d。
  PageRank 最初被用於網頁（具有超連結結構）的Rank（排序處理），但利用圖中的拓撲結構關係，PageRank也可應用於節點的Rank。而且它也為很多重要的圖分析演算法奠定了基礎[15]。

4 結語

  對於大資料時代下各種複雜的大規模圖資料處理問題，研究圖劃分演算法（尤其是基於MapReduce的分散式圖劃分演算法）已展現出巨大的優勢與價值，也具有重大的現實意義，但同時也面臨著眾多的問題與挑戰。藉助分散式計算技術及新興的高速演算法，未來對大規模圖劃分問題的研究必將有重大突破與發展。

參考文獻

[1] Benlic U, Hao J K. Hybrid Metaheuristics for the Graph Partitioning Problem[M]// Hybrid Metaheuristics. 2013:157-185.
[2] 鄭麗麗. 圖劃分演算法綜述[J]. 科技資訊, 2014(4):145-145.
[3] Lipponen,L. Exploring foundations for computer-supported collaborative learning[A]. In Gerry Stahl (Ed.). Computer Support Collaborative Learning: Foundations for a CSCL Community. Proceedings of CSCL 2002.HillsdaIe, New Jersey: Lawrence Erlbaum Associatesjnc.,2002:72-81.
[4] 項國雄, 張小輝. 學習支援服務思想溯源[J]. 中國遠端教育,2005,9.
[5] Dutt S. New faster Kernighan-Lin-type graph-partitioning algorithms[C]// Ieee/acm International Conference on Computer-Aided Design, 1993. Iccad-93. Digest of Technical Papers. 1993:370-377.
[6] Fiduccia C M, Mattheyses R M. A linear-time heuristic for improving network partitions[M]. 1988.
[7] Pothen A, Simon H D, Liou K P. Partitioning sparse matrices with eigenvectors of graphs[J]. Siam Journal on Matrix Analysis & Applications, 1990, 11(3):430-452.
[8] Karypis G, Kumar V. A Fast and High Quality Multilevel Scheme for Partitioning Irregular Graphs[J]. Siam Journal on Scientific Computing, 2006, 20(1):359–392.
[9] 周爽, 鮑玉斌, 王志剛等. BHP:面向BSP模型的負載均衡Hash圖資料劃分, 2013年7月23日[J]. 電腦科學與探索, 2013.
[10] Khayyat Z, Awara K, Jamjoom H, et al. Mizan: Optimizing Graph Mining in Large Parallel Systems[J]. King Abdullah University of Science & Technology, 2012.
[11] Ugander J, Backstrom L. Balanced label propagation for partitioning massive graphs[C]// ACM International Conference on Web Search and Data Mining. 2013:507-516.
[12] Khayyat Z, Awara K, Alonazi A, et al. Mizan: a system for dynamic load balancing in large-scale graph processing[C]// ACM European Conference on Computer Systems. ACM, 2013:169-182.
[13] Vaquero L, Cuadrado F, Logothetis D, et al. xDGP: A Dynamic Graph Processing System with Adaptive Partitioning[J]. Eprint Arxiv, 2013.
[14] Li Jian-Jiang, Jian Cui, Wang Dan, Yan Lin, Huang Yi-Shuang, “Survey of MapReduce Parallel Programming Model”, ACTA ELECTRONICA SINICA, Vol.39, No.11, (2011), pp.2635-2642.
[15] Kleinberg J M. Authoritative Sources in a Hyperlinked Environment[C]// 1999:604–632.